每日OJ题_DFS解决FloodFill⑥_力扣529. 扫雷游戏

力扣529. 扫雷游戏

解析代码

力扣529. 扫雷游戏

529. 扫雷游戏

难度中等

让我们一起来玩扫雷游戏！

给你一个大小为 m x n 二维字符矩阵 board ，表示扫雷游戏的盘面，其中：

'M' 代表一个 未挖出的 地雷，
'E' 代表一个 未挖出的 空方块，
'B' 代表没有相邻（上，下，左，右，和所有4个对角线）地雷的 已挖出的 空白方块，
数字（'1' 到 '8'）表示有多少地雷与这块 已挖出的 方块相邻，
'X' 则表示一个 已挖出的 地雷。

给你一个整数数组 click ，其中 click = [clickr, clickc] 表示在所有 未挖出的 方块（'M' 或者 'E'）中的下一个点击位置（clickr 是行下标，clickc 是列下标）。

根据以下规则，返回相应位置被点击后对应的盘面：

如果一个地雷（'M'）被挖出，游戏就结束了- 把它改为 'X' 。
如果一个 没有相邻地雷 的空方块（'E'）被挖出，修改它为（'B'），并且所有和其相邻的 未挖出 方块都应该被递归地揭露。
如果一个 至少与一个地雷相邻 的空方块（'E'）被挖出，修改它为数字（'1' 到 '8' ），表示相邻地雷的数量。
如果在此次点击中，若无更多方块可被揭露，则返回盘面。

示例 1：

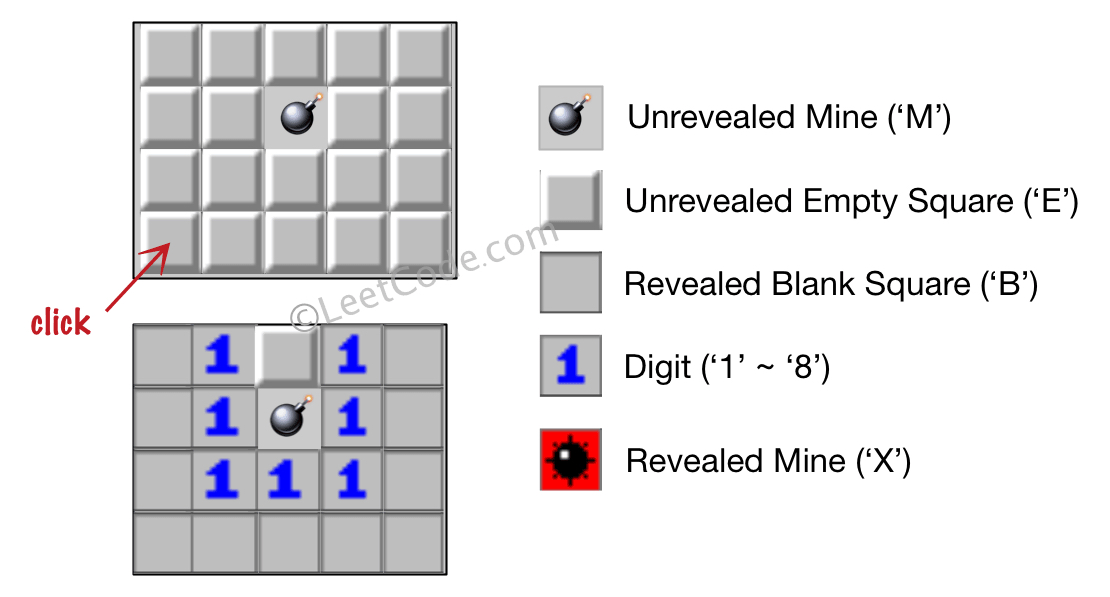
输入：board = [["E","E","E","E","E"],["E","E","M","E","E"],["E","E","E","E","E"],["E","E","E","E","E"]], click = [3,0]
输出：[["B","1","E","1","B"],["B","1","M","1","B"],["B","1","1","1","B"],["B","B","B","B","B"]]

示例 2：

输入：board = [["B","1","E","1","B"],["B","1","M","1","B"],["B","1","1","1","B"],["B","B","B","B","B"]], click = [1,2]
输出：[["B","1","E","1","B"],["B","1","X","1","B"],["B","1","1","1","B"],["B","B","B","B","B"]]

提示：

m == board.length
n == board[i].length
1 <= m, n <= 50
board[i][j] 为 'M'、'E'、'B' 或数字 '1' 到 '8' 中的一个
click.length == 2
0 <= clickr < m
0 <= clickc < n
board[clickr][clickc] 为 'M' 或 'E'

class Solution {
public:vector<vector<char>> updateBoard(vector<vector<char>>& board, vector<int>& click) {}
};

解析代码

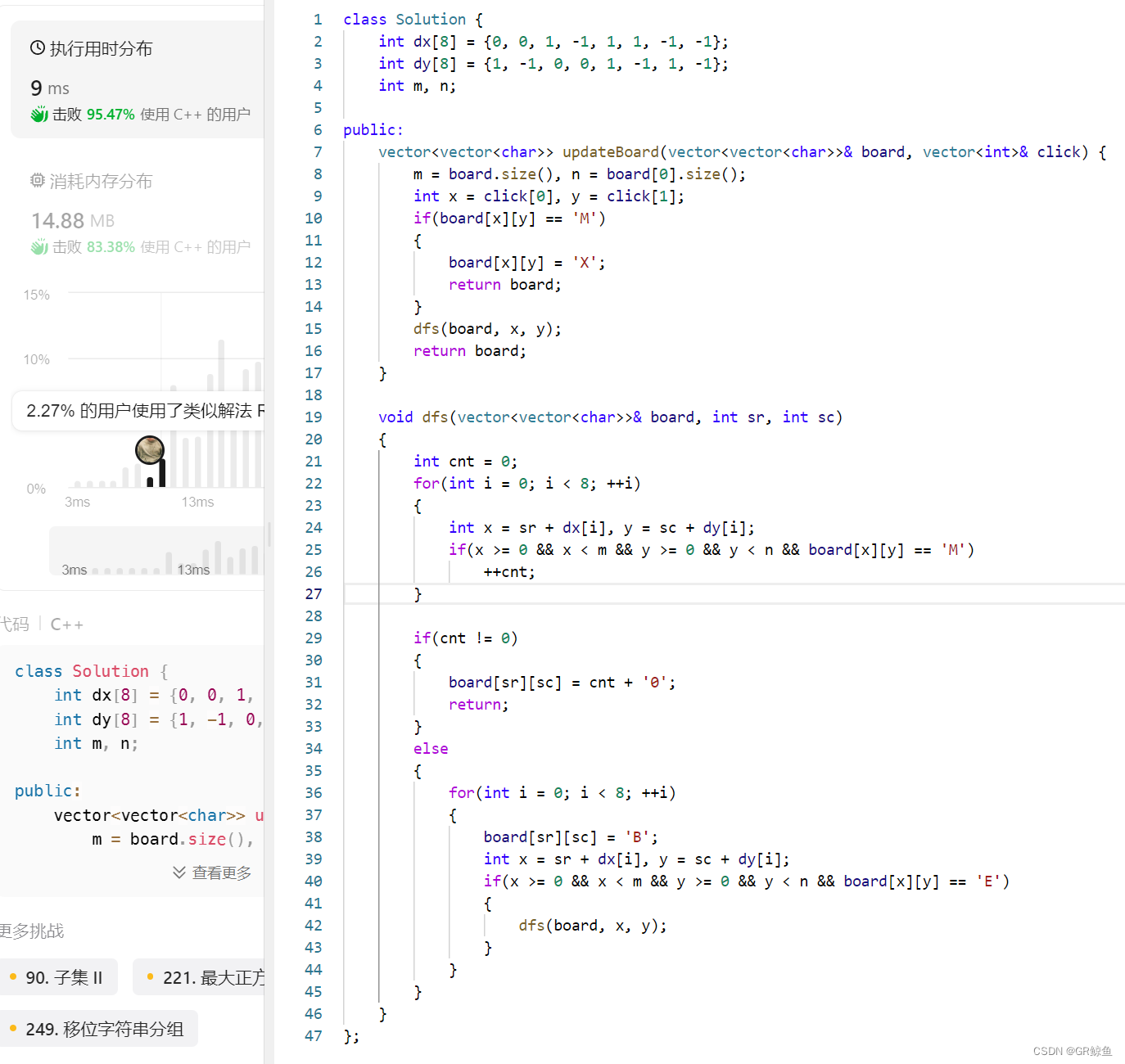
模拟类型的 dfs 题目。首先要搞懂题目要求，也就是游戏规则。从题目所给的点击位置开始，根据游戏规则，来一次 dfs 即可。

dfs大步骤就是统计一下周围的地雷个数，有地雷就在当前位置放上周围地雷的个数，然后返回，没有地雷就改当前位置为没有地雷的空白块B，然后dfs周围的未挖出的空方块E。

class Solution {int dx[8] = {0, 0, 1, -1, 1, 1, -1, -1};int dy[8] = {1, -1, 0, 0, 1, -1, 1, -1};int m, n;public:vector<vector<char>> updateBoard(vector<vector<char>>& board, vector<int>& click) {m = board.size(), n = board[0].size();int x = click[0], y = click[1];if(board[x][y] == 'M'){board[x][y] = 'X';return board;}dfs(board, x, y);return board;}void dfs(vector<vector<char>>& board, int sr, int sc){int cnt = 0;for(int i = 0; i < 8; ++i){int x = sr + dx[i], y = sc + dy[i];if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'M')++cnt;}if(cnt != 0){board[sr][sc] = cnt + '0';return;}else // 周围没地雷{board[sr][sc] = 'B';for(int i = 0; i < 8; ++i){int x = sr + dx[i], y = sc + dy[i];if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'E')dfs(board, x, y); // 再探索周围的空白块}}}
};