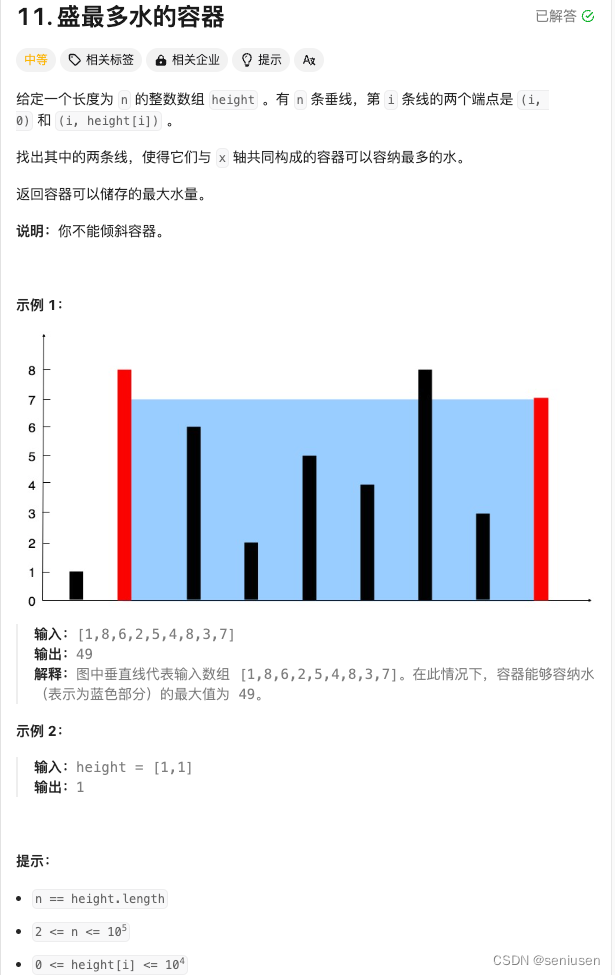
1. 题目

2. 解题思路一

暴力法，遍历所有可能的垂线对 $(i,j)$，求取最大面积：

$$area=min(h[i],h[j])\ast (j-i)$$

注意到，如果垂线 $m$ 在垂线 $i$ 的右边，而且 $h[m]<=h[i]$，那么以垂线 $m$ 为起始的容器我们可以跳过遍历。

为什么呢，假设垂线 $m$ 和垂线 $n$ 组成的容器可以盛的水最多，那么我们把垂线 $m$ 换成垂线 $i$，盛的水肯定会变多。

虽然可以跳过一些循环，代码也通过了测试，但时间复杂度仍然是 $O(n^2)$，应该会有更高效的解决办法。

3. 代码实现一

class Solution {
public:int maxArea(vector<int>& height) {int ret = 0;int max_height = 0;for (int i = 0; i < height.size()-1; ++i) {if (height[i] <= max_height) {continue;}max_height = max(max_height, height[i]);for (int j = i+1; j < height.size(); ++j) {int cur_area = min(height[i], height[j]) * (j - i);ret = max(ret, cur_area);}}return ret;}
};

4. 解题思路二

假设垂线对 $(i,j)$ 组成了一个容器，如果这时候有：

$$h[i]<h[j]，那么有，area=h[i]\ast (j-i)$$

如果这时候我们让垂线 $j$ 往左移动，那么容器的高度不会大于 $h[i]$，而宽度 $<(j-i)$ 会变小，容器面积肯定会变小，所以我们只能让垂线 $i$ 往右移动。

同理，$h[i]>h[j]$ 的时候也只能让垂线 $j$ 往左移动，也就是，只能是高度较低的垂线向高度较高的垂线移动。

5. 代码实现二

class Solution {
public:int maxArea(vector<int>& height) {int i = 0;int j = height.size() - 1;int ret = 0;while (i != j) {ret = max(ret, min(height[i], height[j]) * (j - i));if (height[i] <= height[i]) {++i;} else {--j;}}return ret;}
};