普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储 。

一、堆的概念及结构

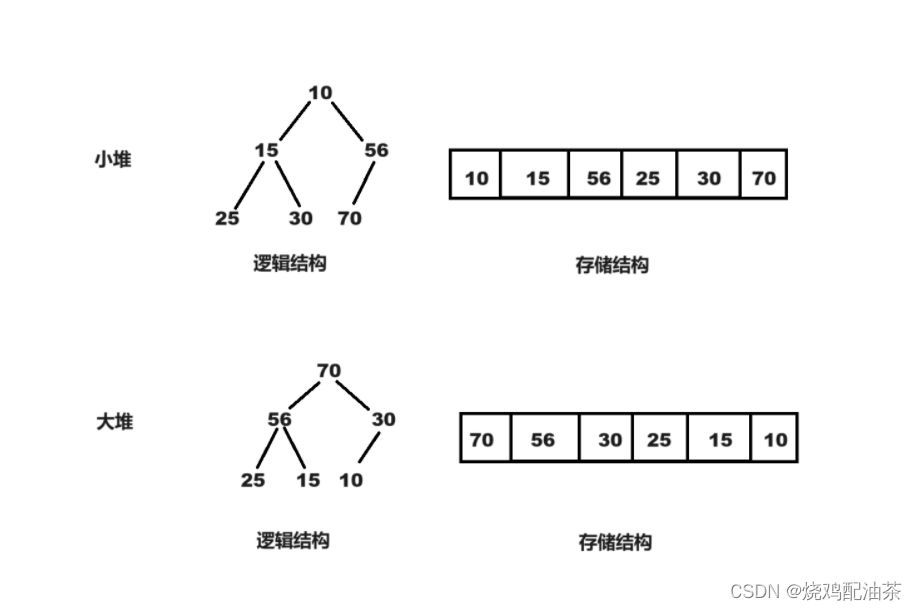
父节点比孩子结点大 是大堆

父节点比孩子结点小 是小堆

堆的性质

堆中某个节点的值总是不大于或不小于其父节点的值

堆总是一棵完全二叉树。

二、堆的实现

接口函数

//Heap.h
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int HPDataType;
typedef struct Heap
{HPDataType* _a;int _size;int _capacity;
}Heap;// 堆的构建
void HeapCreate(Heap* hp);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
bool HeapEmpty(Heap* hp);

函数实现

//Heap.c
#include"Heap.h"
// 小堆
// 堆的构建
void HeapCreate(Heap* hp)
{assert(hp);hp->_a = NULL;hp->_size = 0;hp-> _capacity = 0;
}
// 堆的销毁
void HeapDestory(Heap* hp)
{assert(hp);free(hp->_a);hp->_a = NULL;hp->_size = 0;hp->_capacity = 0;
}
void swap(HPDataType* pa, HPDataType* pb)
{HPDataType tmp = *pa;*pa = *pb;*pb = tmp;
}
void AdjustUp(Heap* hp, int child)
{int parent = (child - 1) / 2;while (child > 0){if (hp->_a[child] < hp->_a[parent]){swap(&hp->_a[child], &hp->_a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}// 堆的插入   插入后 为了使堆满足依然是小堆的条件 将插入的数向上调整
void HeapPush(Heap* hp, HPDataType x)
{assert(hp);if (hp->_size == hp->_capacity){int newcapacity = hp->_capacity == 0 ? 4 : hp->_capacity * 2;HPDataType* tmp = (HPDataType*)realloc(hp->_a, newcapacity * sizeof(HPDataType));if (tmp == NULL){perror("realloc fail");exit(-1);}hp->_a = tmp;hp->_capacity = newcapacity;}hp->_a[hp->_size] = x;hp->_size++;//向上调整AdjustUp(hp,hp->_size-1);
}
void AdjustDown(Heap* hp)
{int parent = 0;int child = 2 * parent + 1;while (child <= hp->_size-1){//假设法 左孩子是较小的孩子 如果不是 更新一下if (hp->_a[child] > hp->_a[child + 1]){child++;}//比较 较小孩子与父节点大小 如果 较小孩子比父节点小 则交换if (hp->_a[child] < hp->_a[parent]){//较小孩子 与 父节点交换swap(&hp->_a[parent], &hp->_a[child]);}else{break;}//更新父节点、孩子节点 下标parent = child;child = 2 * parent + 1;}
}
// 堆的删除 （删除的是堆顶 -> 找 次大or次小）
//堆顶数据先与最后一个结点交换 交换到堆顶的数据 向下调整
void HeapPop(Heap* hp)
{assert(hp);assert(hp->_size > 0);//堆顶数据与最后一个数据 交换swap(&hp->_a[0],&hp->_a[hp->_size - 1]);//删除此时的最后一个数据（堆顶）hp->_size--;//将 新的堆顶向下调整 AdjustDown(hp);
}
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{assert(hp);assert(hp->_size > 0);return hp->_a[0];
}
// 堆的数据个数
int HeapSize(Heap* hp)
{assert(hp);return hp->_size;
}
// 堆的判空
bool HeapEmpty(Heap* hp)
{assert(hp);return hp->_size == 0;
}

测试函数功能

//test.c
#include"Heap.h"
int main()
{Heap hp;HeapCreate(&hp);HPDataType a[] = { 2, 4, 9, 1, 12, 0, 5, 3, 7 };for (int i = 0; i < sizeof(a) / sizeof(HPDataType); i++){HeapPush(&hp, a[i]);}while (!HeapEmpty(&hp)){printf("%d ", HeapTop(&hp));HeapPop(&hp);}printf("\n");HeapDestory(&hp);return 0;
}