代码随想录day19day20打卡

二叉树

1 二叉树的最大深度和最小深度

最大深度已经学习过了，实质就是递归的去判断左右子节点的深度，然后对其进行返回。
附加两个学习的部分：
（1）使用前序遍历的方法求解

int result;
void getdepth(TreeNode* node, int depth){result = depth > result ? depth : result;if(node->left == NULL && node->right==NULL)return ;if(node->left){ //左节点深度depth++; //深度+1getdepth(node->left, depth);depth--; //此处需要进行回溯}if(node->right){depth++;getdepth(node->right, depth);depth--; //此处需要进行回溯	}return ;
}
int maxDepth(TreeNode* root){result = 0;if(root == NULL)return result;getdepth(root,1);return result;
}

(2)迭代法，使用层序遍历
即只需要记录遍历的层数即可

int maxDepth(TreeNode* root){if(root == NULL)return 0;int depth = 0;queue<TreeNode*> que;que.push(root);while(!que.empty()){int size = que.size();depth++;for(int i = 0;i<size;i++){TreeNode* node = que.front();que.pop();if(node->left)que.push(node->left);if(node->right)que.push(node->right);}}return depth;
}

最小深度题目：
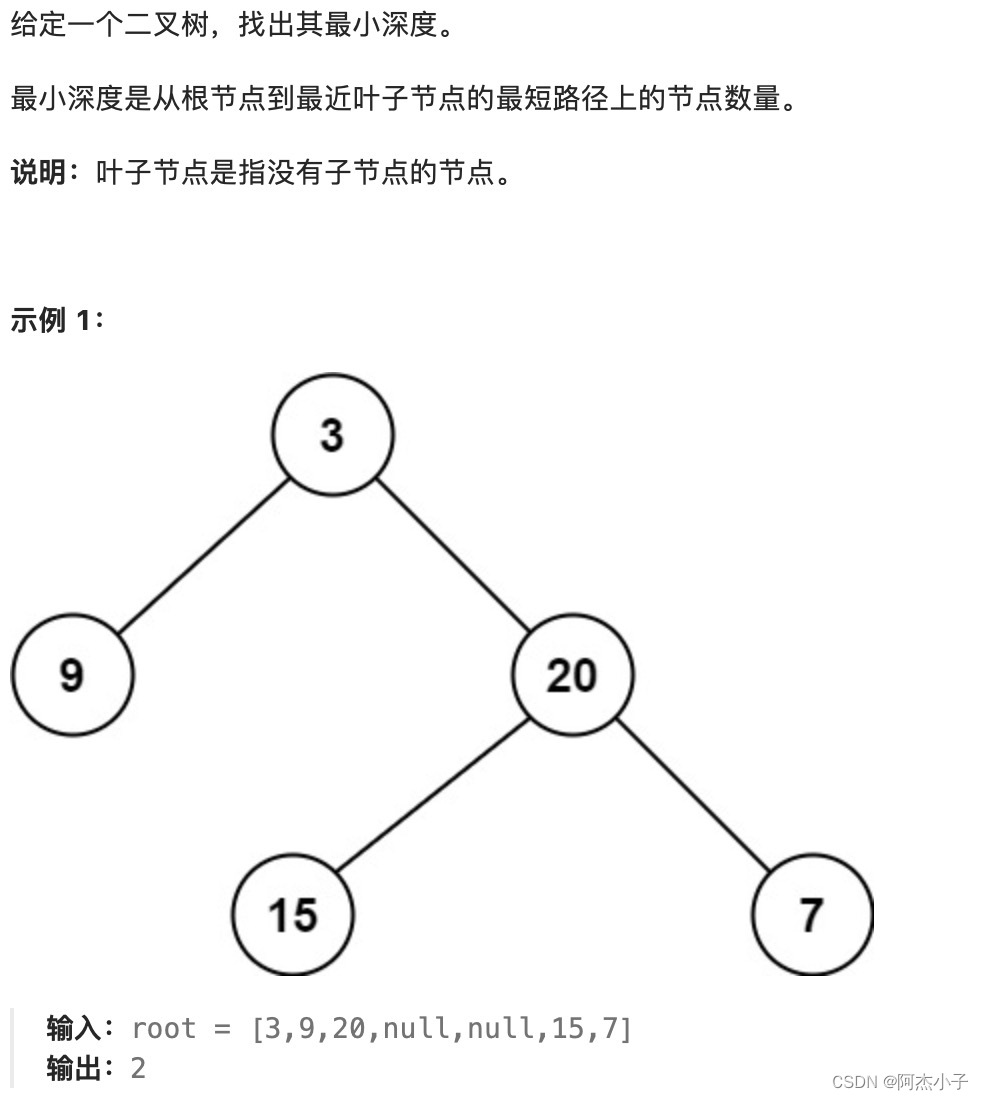
在这里插入图片描述

在递归法当中，要注意左子树不存在或者是右子树不存在的问题，其余的按照最大深度的模版套用即可。

//后序遍历
int getDepth(TreeNode* node){if(node == NULL)return 0;int leftDepth = getDepth(node->left);int rightDepth = getDepth(node->right);//左空右不空if(node->left == NULL && node->right != NULL){return 1+rightDepth;}//右空左不空if(node->left != NULL && node->right == NULL){return 1+leftDepth;}if(node->left != NULL && node->right != NULL){return 1+min(leftDepth,rightDepth);}
}
int minDepth(TreeNode* root){return getDepth(root);
}//前序遍历
class Solution {
private:int result;void getdepth(TreeNode* node, int depth) {// 函数递归终止条件if (node == nullptr) {return;}// 中，处理逻辑：判断是不是叶子结点if (node -> left == nullptr && node->right == nullptr) {result = min(result, depth);}if (node->left) { // 左getdepth(node->left, depth + 1);}if (node->right) { // 右getdepth(node->right, depth + 1);}return ;}public:int minDepth(TreeNode* root) {if (root == nullptr) {return 0;}result = INT_MAX;getdepth(root, 1);return result;}
};

迭代法只需增加一个条件，就是到这个节点时，左右子都为空，那么可以返回这个深度。

int minDepth(TreeNode* root) {if (root == NULL) return 0;int depth = 0;queue<TreeNode*> que;que.push(root);while(!que.empty()) {int size = que.size();depth++; // 记录最小深度for (int i = 0; i < size; i++) {TreeNode* node = que.front();que.pop();if (node->left) que.push(node->left);if (node->right) que.push(node->right);if (!node->left && !node->right) { // 当左右孩子都为空的时候，说明是最低点的一层了，退出return depth;}}}return depth;}

2 完全二叉树的节点个数

3 平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过1。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]
返回true

复习二叉树节点的深度和高度。

二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数
二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数。

一般定义根节点的深度为1。求深度可以从上到下进行查找，需要进行前序遍历（中左右）。而求高度只能从下到上去查，所以只能后序遍历（左右中）。

回顾求取二叉树的最大深度

class solution{
public:int result;void getDepth(TreeNode* node, int depth){result = depth > reusult ? depth : result;if(node->left == NULL && node->right == NULL) return ;if(node->left){depth++;getDepth(node->left,depth);depth--;}if(node->right){depth++;getDepth(node->right,depth);depth--;}return ;}int maxDepth(TreeNode* root){result = 0;if(root == NULL)return result;getDepth(root, 1);return result;}
};

递归法
1）明确递归函数的参数和返回值：那么参数一定是当前的节点，并且需要返回以当前传入节点为根节点的树的高度。int getHeight(TreeNode* node)
2）终止条件：既需要遇到空节点。if(node==NULL) return 0;
3）确认单层递归的逻辑：只需要判断左子树和右子树的高度差即可。

int leftHeight = getHeight(node->left);
if(leftHeight == -1)return -1;
int rightHeight= getHeight(node->right);
if(rightHeight== -1)return -1;
int result;
if(ans(leftHeight - rightHeight) > 1) return -1;
else result = 1 + max(leftHeight,rightHeight);
return result;

最终代码：

class Solution {
public:// 返回以该节点为根节点的二叉树的高度，如果不是平衡二叉树了则返回-1int getHeight(TreeNode* node) {if (node == NULL) {return 0;}int leftHeight = getHeight(node->left);if (leftHeight == -1) return -1;int rightHeight = getHeight(node->right);if (rightHeight == -1) return -1;return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);}bool isBalanced(TreeNode* root) {return getHeight(root) == -1 ? false : true;}
};

4 二叉树的所有路径（回溯算法）

给定一个二叉树，返回所有从根节点到叶子节点的路径。

说明: 叶子节点是指没有子节点的节点。

在这里插入图片描述
要求从根节点到叶子的路径，所以需要前序遍历，这样才方便让父节点指向孩子节点，找到对应的路径。

在这道题目中将第一次涉及到回溯，因为我们要把路径记录下来，需要回溯来回退一个路径再进入另一个路径。

前序遍历以及回溯的过程如图：
加粗样式
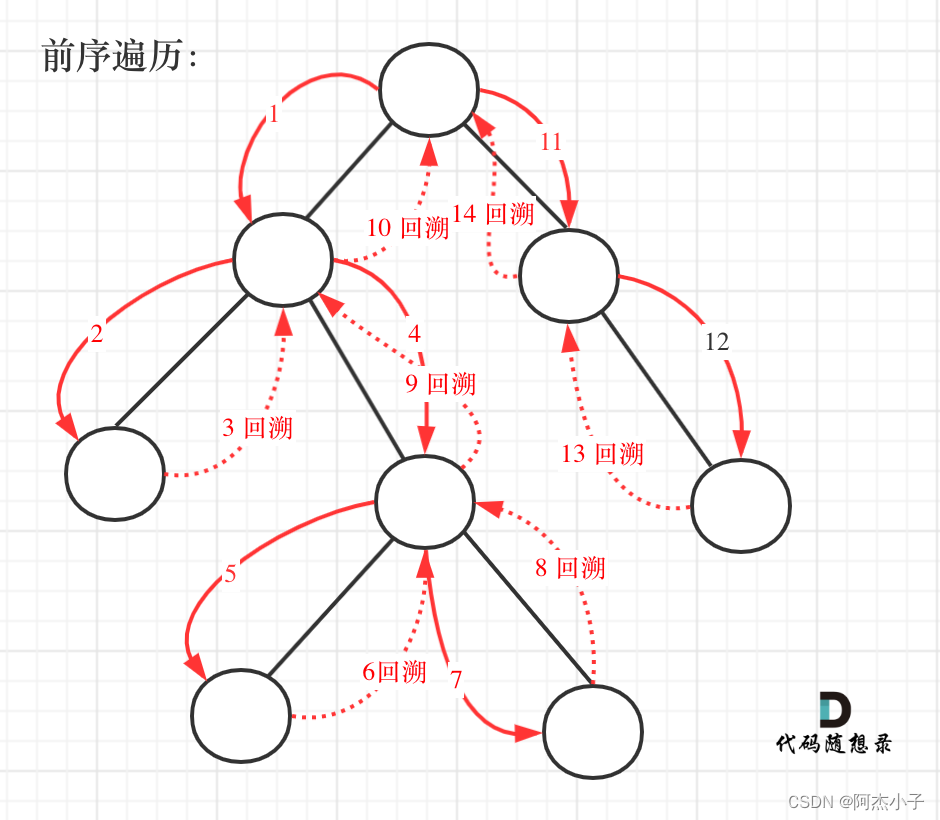
递归回溯法
1）明确递归函数的参数和返回值：需要传入根节点，记录每一条路径的path以及结果集result，不需要返回值。
2）终止条件：既需要遇到节点的左右子均为空。当遇到这个情况的时候，需要将之前遍历的节点存入数组当中，并且还需要将其转化为string，存入result。
3）确认单层递归的逻辑：即遍历过程中需要将遍历的path存入数组，因为是前序遍历，需要先处理中间节点，中间节点就是我们要记录路径上的节点，先放进path中。path.push_back(cur->val);
然后是递归和回溯的过程，上面说过没有判断cur是否为空，那么在这里递归的时候，如果为空就不进行下一层递归了。所以递归前要加上判断语句，下面要递归的节点是否为空，同时需要进行回溯，也就是要把这个path弹出去，如下：

if (cur->left) {traversal(cur->left, path, result);path.pop_back(); // 回溯
}
if (cur->right) {traversal(cur->right, path, result);path.pop_back(); // 回溯
}

整体的代码如下：

class Solution {
private:void traversal(TreeNode* cur, vector<int>& path, vector<string>& result) {path.push_back(cur->val); // 中，中为什么写在这里，因为最后一个节点也要加入到path中 // 这才到了叶子节点if (cur->left == NULL && cur->right == NULL) {string sPath;for (int i = 0; i < path.size() - 1; i++) {sPath += to_string(path[i]);sPath += "->";}sPath += to_string(path[path.size() - 1]);result.push_back(sPath);return;}if (cur->left) { // 左 traversal(cur->left, path, result);path.pop_back(); // 回溯}if (cur->right) { // 右traversal(cur->right, path, result);path.pop_back(); // 回溯}}public:vector<string> binaryTreePaths(TreeNode* root) {vector<string> result;vector<int> path;if (root == NULL) return result;traversal(root, path, result);return result;}
};

代码精简：

class Solution {
private:void traversal(TreeNode* cur, string path, vector<string>& result) {path += to_string(cur->val); // 中if (cur->left == NULL && cur->right == NULL) {result.push_back(path);return;}if (cur->left) traversal(cur->left, path + "->", result); // 左if (cur->right) traversal(cur->right, path + "->", result); // 右}public:vector<string> binaryTreePaths(TreeNode* root) {vector<string> result;string path;if (root == NULL) return result;traversal(root, path, result);return result;}
};

5 左叶子之和

计算给定二叉树的所有左叶子之和。

示例：

在这里插入图片描述
判断当前节点是不是左叶子是无法判断的，必须要通过节点的父节点来判断其左孩子是不是左叶子。

如果该节点的左节点不为空，该节点的左节点的左节点为空，该节点的左节点的右节点为空，则找到了一个左叶子

递归回溯法
1）明确递归函数的参数和返回值：需要传入根节点，返回值为数值之和
2）终止条件：遇到空节点，返回0。
3）确认单层递归的逻辑：遇到左叶子存入该值，然后通过递归求取左子树左叶子之和与右子树左叶子之和。

int sumOfLeftLeaves(TreeNode* root) {if (root == NULL) return 0;if (root->left == NULL && root->right== NULL) return 0;int leftValue = sumOfLeftLeaves(root->left);    // 左if (root->left && !root->left->left && !root->left->right) { // 左子树就是一个左叶子的情况leftValue = root->left->val;}int rightValue = sumOfLeftLeaves(root->right);  // 右int sum = leftValue + rightValue;               // 中return sum;}