437. 路径总和 III - 力扣(LeetCode)
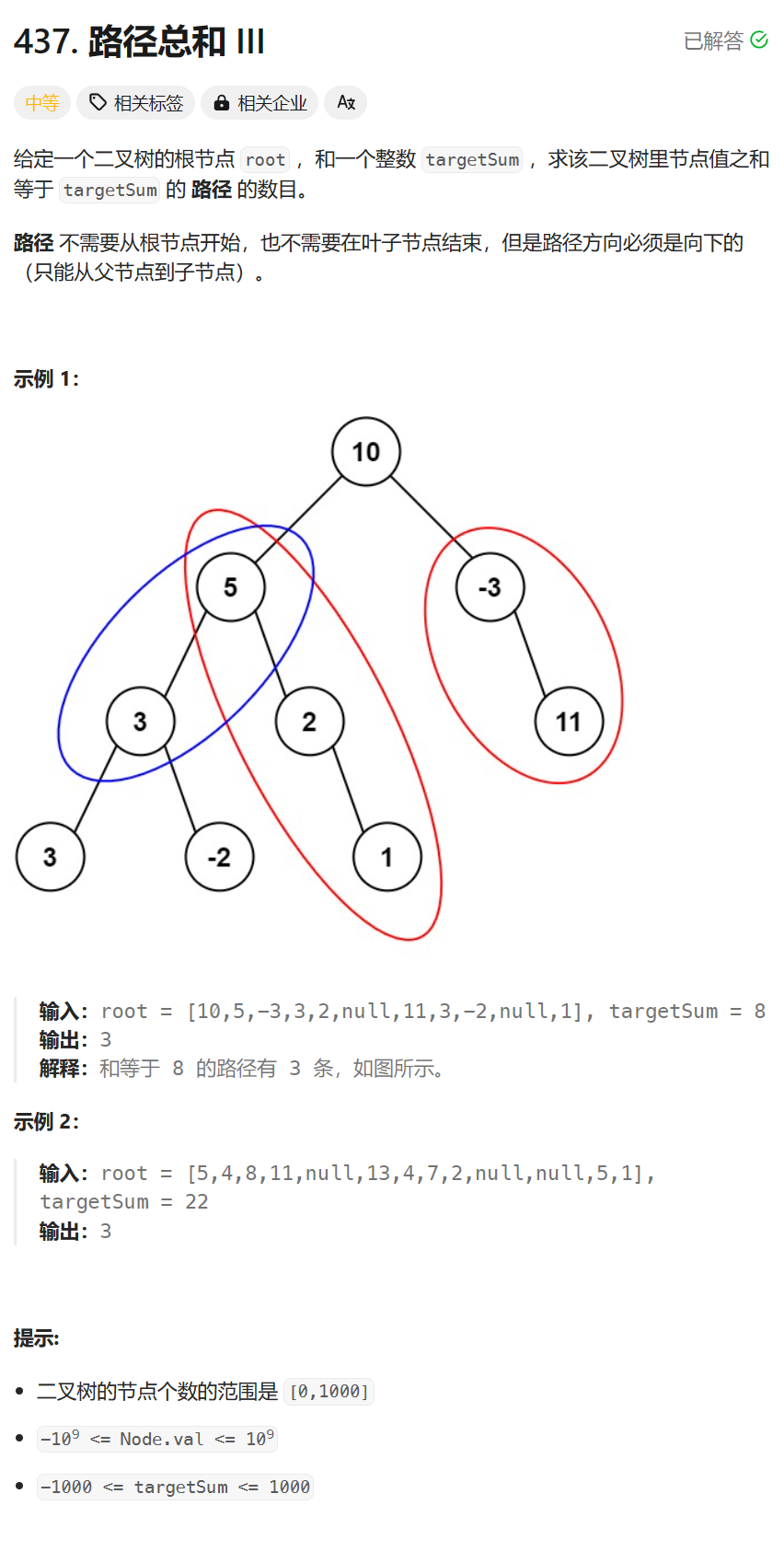
前序遍历时,维护当前路径(根节点开始)的路径和,同时记录路径上每个节点的路径和
假设当前路径和为cur,那么ans += 路径和(cur - target)的出现次数
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:unordered_map<long long, int> mp;long long ans = 0;long long t;void dfs(TreeNode *root, long long &cur) {if (root == nullptr) return;cur += root->val;ans += mp[cur - t] ;mp[cur] ++ ;dfs(root->left, cur);dfs(root->right, cur);mp[cur] -- ;cur -= root->val;}int pathSum(TreeNode* root, int targetSum) {mp[0] ++ ;t = targetSum;long long cur = 0;dfs(root, cur);return ans;}
};
105. 从前序与中序遍历序列构造二叉树 - 力扣(LeetCode)
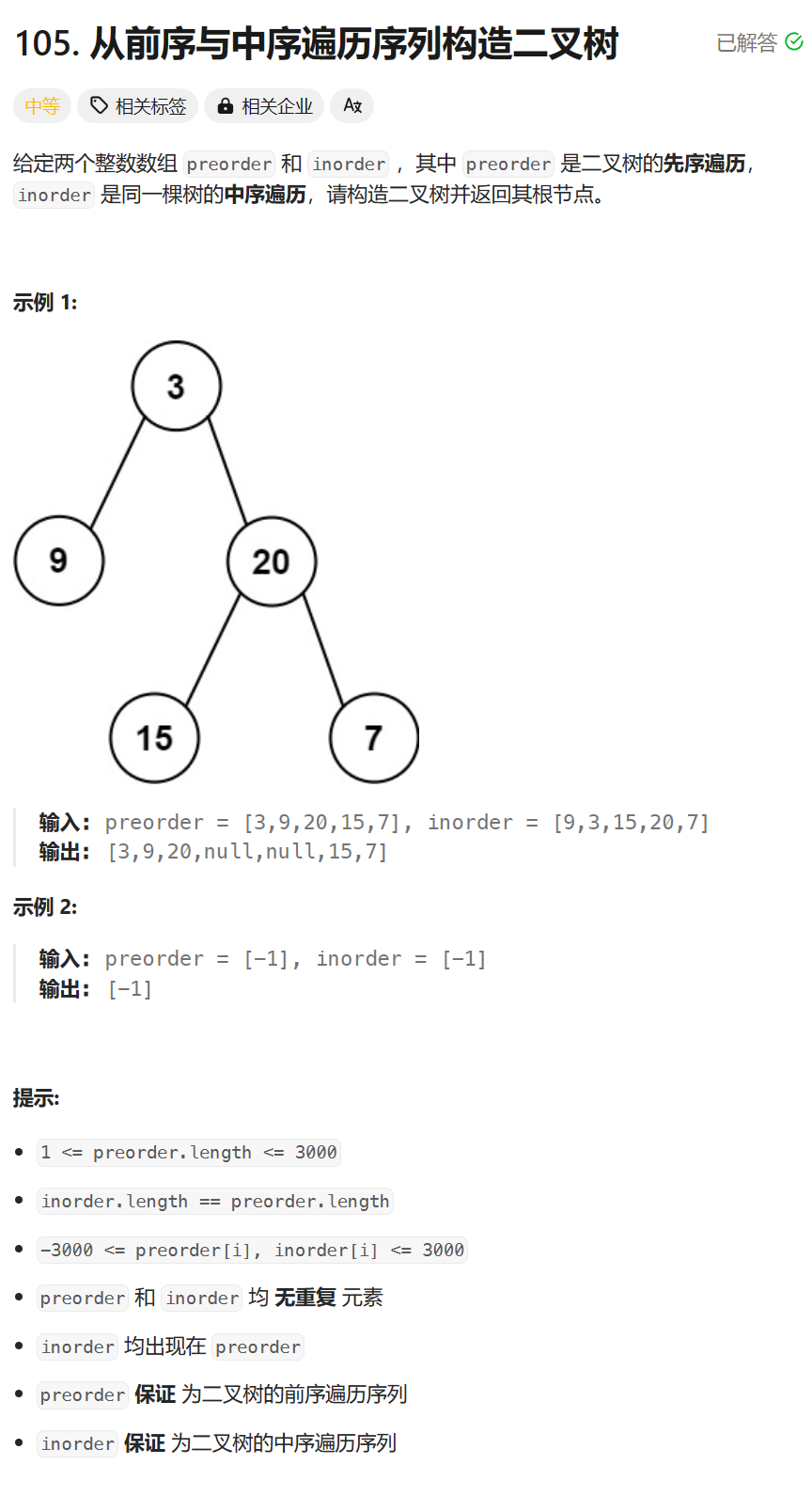
递归构造,每次构造子树的根节点
根节点的左右子节点如何构造?根据中序遍历中,根节点的位置确定左右子树节点数量
在前序遍历中,分别确定左右子树节点的范围,两者的第一个节点就是根节点的左右节点
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),* right(right) {}* };*/
class Solution {
public:unordered_map<int, int> mp;TreeNode* dfs(vector<int> &preorder, vector<int> &inorder, int l, int r, int ll, int rr) {if (l > r) return nullptr;TreeNode *root = new TreeNode(preorder[l]);int iidx = mp[preorder[l]];int sz = iidx - ll;root->left = dfs(preorder, inorder, l + 1, l + sz, ll, iidx - 1);root->right = dfs(preorder, inorder, l + sz + 1, r, iidx + 1, rr);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int n = preorder.size();for (int i = 0; i < inorder.size(); ++ i)mp[inorder[i]] = i;return dfs(preorder, inorder, 0, n - 1, 0, n - 1);}
};



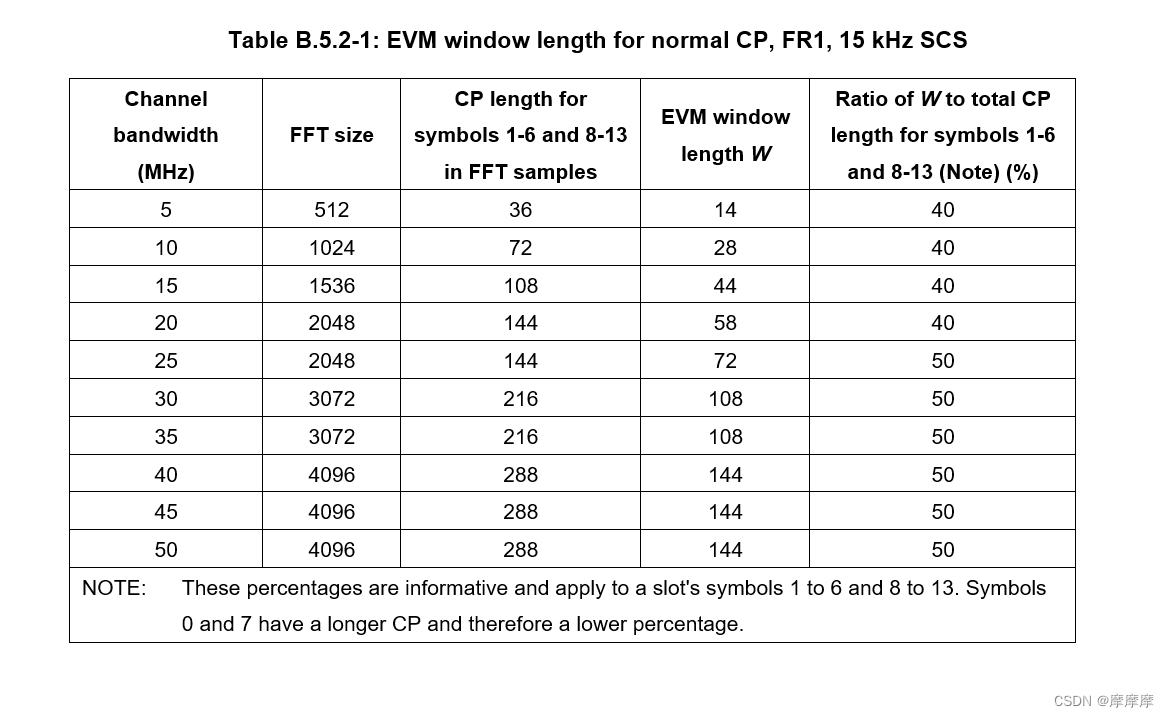
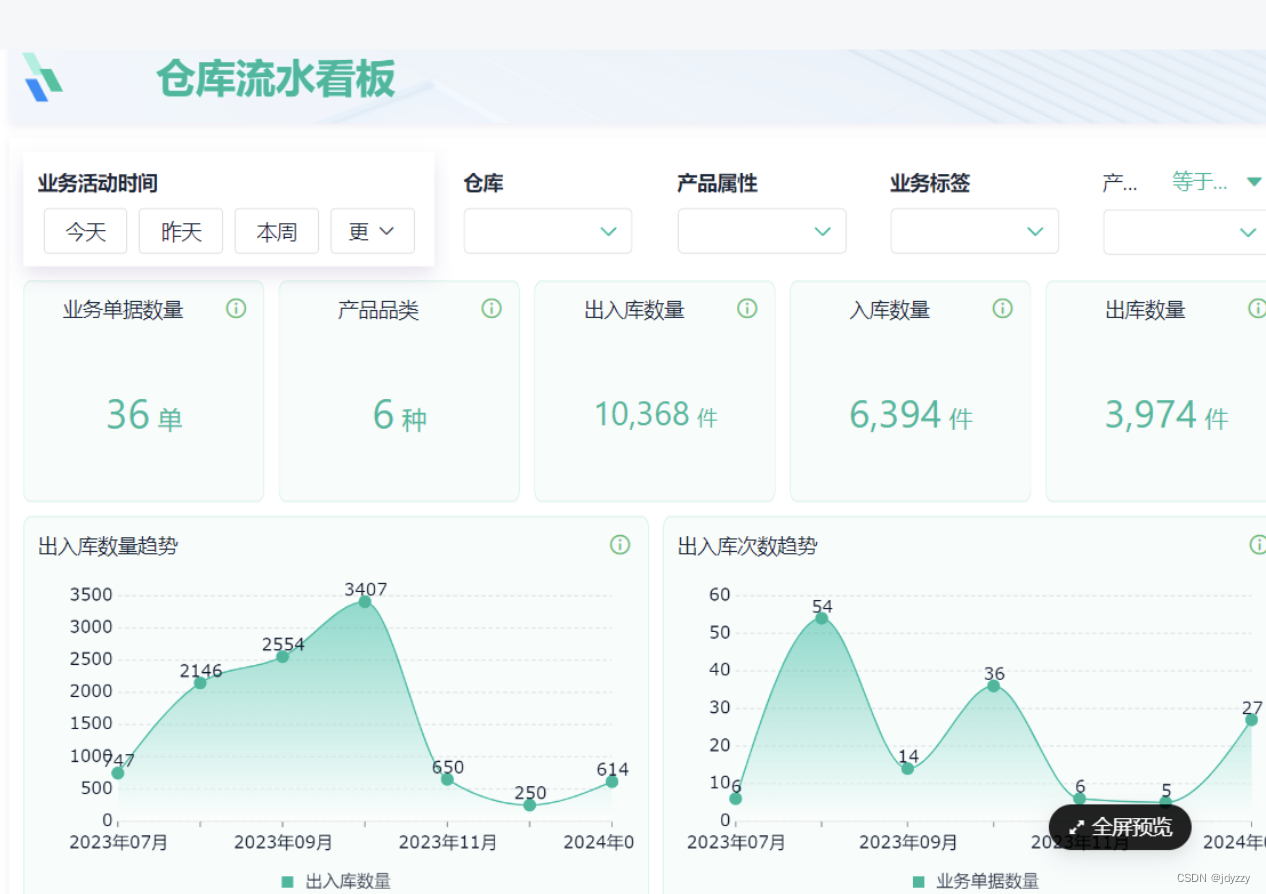


![[vue] nvm](https://img-blog.csdnimg.cn/direct/8d8f3c4cc22747658dcd267f9f6298a6.png)


