相机模型的内参、外参
文章目录
- 相机模型的内参、外参
- 1. 针孔模型、畸变模型(内参)
- 2. 手眼标定(外参)
- Reference
这篇笔记主要参考:slam十四讲第二版(高翔)
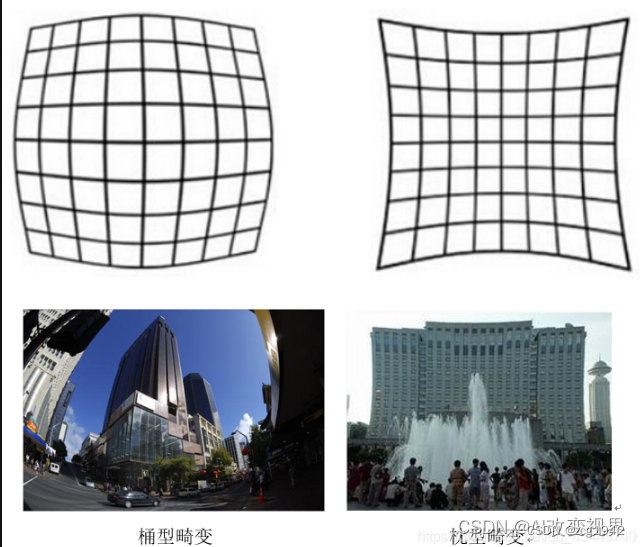
相机将三维世界中的坐标点(单位为米)映射到二维的像素平面(单位为像素)的过程能够使用一个几何模型来进行描述,为了简单起见这个模型我们通常使用针孔模型。同时,由于相机镜头上透镜的存在,透镜的安装不能保证绝对的准确,因此在成像的过程中还会出现畸变。因此,我们使用针孔模型和畸变模型来描述整个投影过程。
针孔模型和畸变模型能够把外部的三维点投影到相机内部的成像平面,这组参数就构成了相机的内参(intrinsics)
1. 针孔模型、畸变模型(内参)
针孔模型可以用中学学习的小孔呈现原理来进行解释,如下图所示,

图中包括两个坐标系,一个是相机内部的物理成像平面坐标系 O ′ − x ′ − y ′ O^\prime-x^\prime-y^\prime O′−x′−y′,这是一个二维的坐标系,还有一个是以相机的光心为中心的相机坐标系 O − x − y − z O-x-y-z O−x−y−z,这是一个三维坐标系。根据小孔成像原理,现实世界中的 P P P点在经过小孔 O O O投影之后,落在物理平面 O ′ − x ′ − y ′ O^\prime-x^\prime-y^\prime O′−x′−y′上,成像点为 P ′ P^\prime P′,设 P P P的坐标为 [ X , Y , Z ] T [X,Y,Z]^T [X,Y,Z]T, P ′ = [ X ′ , Y ′ , Z ′ ] T P^\prime=[X^\prime,Y^\prime,Z^\prime]^T P′=[X′,Y′,Z′]T,并且设物理成像平面到小孔的距离为 f f f(焦距),那么根据三角形的相似原理,我们很容易得到如下的等式:
Z f = − X X ′ = − Y Y ′ \frac{Z}{f} = - \frac{X}{X^\prime} = - \frac{Y}{Y^\prime} fZ=−X′X=−Y′Y
为了让模型更符合实际,我们可以利用算法等价地把成像平面对称地放到相机的前方,和三维空间点一起放在相机坐标系的同一侧,如图所示:
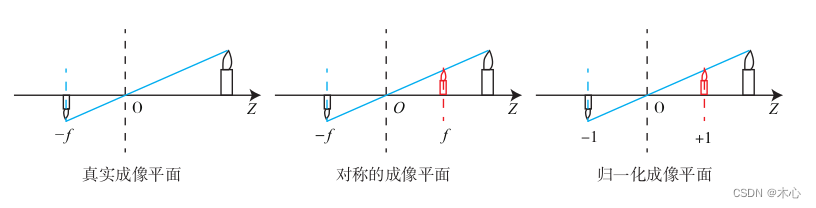
这样我们就可以把负号去掉了,使式子更加简洁
Z f = X X ′ = Y Y ′ X ′ = f X Z Y ′ = f Y Z \begin{align*} \frac{Z}{f} & = \frac{X}{X^\prime} = \frac{Y}{Y^\prime} \\ X^\prime & = f\frac{X}{Z} \\ Y^\prime & = f\frac{Y}{Z} \end{align*} fZX′Y′=X′X=Y′Y=fZX=fZY
上式描述了点 P P P和它的像之间的空间关系,这里的所有单位都可以用米(m)来表示。不过在最终的相机中,我们获得的是一个个的像素,这需要我们在成像平面上进行采样和量化。为了描述传感器将感受到的光线转换成图片像素的过程,我们设在物理成像平面上固定着一个像素平面 o − u − v o-u-v o−u−v,如下图所示
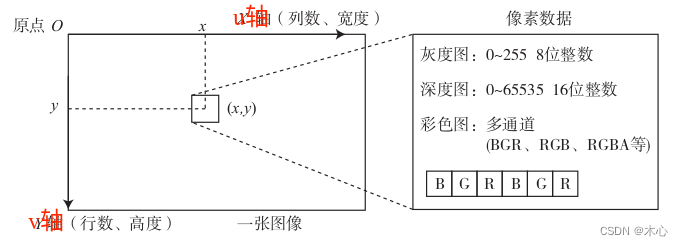
像素坐标系通常的定义方式为:原点 o o o位于图像的左上角, u u u轴和 x x x轴平行, v v v轴向下和 y y y轴平行,像素坐标系和成像平面之间相差了一个缩放和一个原点的平移。我们假设现像素平面下的坐标 P ′ = [ u , v ] T P^\prime=[u,v]^T P′=[u,v]T。设像素坐标在 u u u轴上缩放了 α \alpha α倍,在 v v v轴上缩放了 β \beta β倍,同时原点移动了 [ c x , c y ] T [c_x,c_y]^T [cx,cy]T,这样 P ′ P^\prime P′在成像坐标系下的坐标 [ X ′ , Y ′ ] T [X^\prime,Y^\prime]^T [X′,Y′]T与像素坐标系下的坐标 [ u , v ] T [u,v]^T [u,v]T具有如下的关系:
{ u = α X ′ + c x v = β Y ′ + c y \left\{ \begin{align*} u & = \alpha X^\prime + c_x \\ v & = \beta Y^\prime + c_y \end{align*} \right. {uv=αX′+cx=βY′+cy
代入之前的关系,有下式
{ u = α f X Z + c x v = β f Y Z + c y \left\{ \begin{align*} u & = \alpha f\frac{X}{Z} + c_x \\ v & = \beta f\frac{Y}{Z}+ c_y \end{align*} \right. ⎩ ⎨ ⎧uv=αfZX+cx=βfZY+cy
然后把 α f \alpha f αf合并为 f x f_x fx,把 β f \beta f βf合并为 f y f_y fy,得:
{ u = f x X Z + c x v = f y Y Z + c y \left\{ \begin{align*} u & = f_x\frac{X}{Z} + c_x \\ v & = f_y\frac{Y}{Z}+ c_y \end{align*} \right. ⎩ ⎨ ⎧uv=fxZX+cx=fyZY+cy
其中, f f f的单位为米, α , β \alpha, \beta α,β的单位为像素/米。再将上式写成齐次的形式
[ u v 1 ] = 1 Z [ f x 0 c x 0 f y c y 0 0 1 ] [ X Y Z ] ≜ 1 Z K P \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \frac{1}{Z} \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \end{bmatrix} \triangleq \frac{1}{Z}\bold{K}\bold{P} uv1 =Z1 fx000fy0cxcy1 XYZ ≜Z1KP
然后再将 Z Z Z移到左边
Z [ u v 1 ] = [ f x 0 c x 0 f y c y 0 0 1 ] [ X Y Z ] ≜ K P Z\begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \end{bmatrix} \triangleq \bold{K}\bold{P} Z uv1 = fx000fy0cxcy1 XYZ ≜KP
其中,我们将中间量组成的矩阵 K \bold{K} K称为相机的内参矩阵(Camera Intrinsics)。 K \bold{K} K通常认为,相机的内参在出厂之后就已经固定好了,不会在使用的过程中发生变化,有时 K \bold{K} K是由厂家提供,有时 K \bold{K} K需要自己进
有了内参矩阵 K \bold{K} K,我们就可以通过确定像素点的坐标 P u v P_{uv} Puv,来反算出点 P P P在相机坐标系中的位置 [ X , Y , Z ] T [X,Y,Z]^T [X,Y,Z]T,然后通过这个位置就可以计算出点 P P P在世界坐标系world中的坐标 P w P_w Pw了。
相机的畸变模型,这里不再介绍了,感兴趣的可以去看原书。
2. 手眼标定(外参)
相机的外参一般指的是从相机坐标系到机器人的基坐标系的齐次变换矩阵,当然这个齐次变换矩阵也可以用旋转矩阵 R \bold{R} R和平移向量来进行描述 t \bold{t} t,有下式成立
Z P u v = Z [ u v 1 ] = K ( R P w + t ) = K T P w ZP_{uv} = Z \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \bold{K}(\bold{R}P_w + \bold{t}) = \bold{K}\bold{T}P_w ZPuv=Z uv1 =K(RPw+t)=KTPw
这个在以后的博客中再详细介绍。
Reference
[1]slam十四讲第二版(高翔)