目录
1. 激活函数不是阶跃函数
1.1 激活函数和阶跃函数都是非线性函数
1.2 激活函数不是阶跃函数
2. sigmoid 函数
2.1 sigmoid 函数表达式
2.2 sigmoid 函数 Python 实现
2.4 sigmoid 函数图
3. ReLU 函数
3.1 ReLU 函数表达式
3.2 ReLU 函数 Python 实现
3.4 ReLU 函数图
在下面的文章中提到了激活函数,事实上激活函数有很多种,本文介绍两种最常见的。另外文章中可能会用到一些 numpy、Matplotlib 模块的知识,同学们如果没有了解可以看看下面的文章。
4. 从感知机到神经网络-CSDN博客
1. 介绍 Matplotlib-CSDN博客
Python 数据分析_江南野栀子的博客-CSDN博客
1. 激活函数不是阶跃函数
1.1 激活函数和阶跃函数都是非线性函数
在这里我们会提到数学上的专有名词 “线性函数” 和 “非线性函数”,两者是相对的。不是线性函数,就是非线性函数。
激活函数和阶跃函数都是非线性函数。线性和非线性是相对而言的,它们是用来区分函数 y = f(x) 对自变量 x 的依赖关系的。
-
线性:如果函数 y = f(x) 满足以下两个条件,那么它就是一个线性函数:
-
叠加原理成立,即 f(ax + by) = af(x) + bf(y),其中 a 和 b 是任意常数。
-
齐次原理成立,即 f(kx) = kf(x),其中 k 是任意常数。
-
-
非线性:如果函数 y = f(x) 不满足以上两个条件,那么它就是一个非线性函数。
从几何上看,线性函数的图像是一条直线,而非线性函数的图像是一条曲线或者不连续的线段。但是请注意,图像是一条直线的不一定是线性函数。
严格来说,只有过原点的最简单的直线f(x)=kx才被称为一元线性函数;f(x)=kx+b 这种函数是不能满足叠加原理和齐次原理的。但是 f(x)=kx+b 的图是一条直线!
1.2 激活函数不是阶跃函数
激活函数不是阶跃函数,阶跃函数的图是两条直线。激活函数的图是曲线的。
阶跃函数适用于感知机,激活函数适用于神经网络,但是感知机的初级模型和神经网络的神经元图模型非常相似,仅此而已。
下面是阶跃函数的 python 代码实现和图。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
def step_function(x):return(np.array(x>0,dtype=np.int32))
x=np.arange(-5.0,5.0,0.1)
y=step_function(x)
plt.plot(x,y)
plt.xlabel("x line")
plt.ylabel("y line")
plt.xlim(-5,5.1) #指定 x 轴的位置
plt.ylim(-1,1.1) #指定 y 轴的位置
plt.show()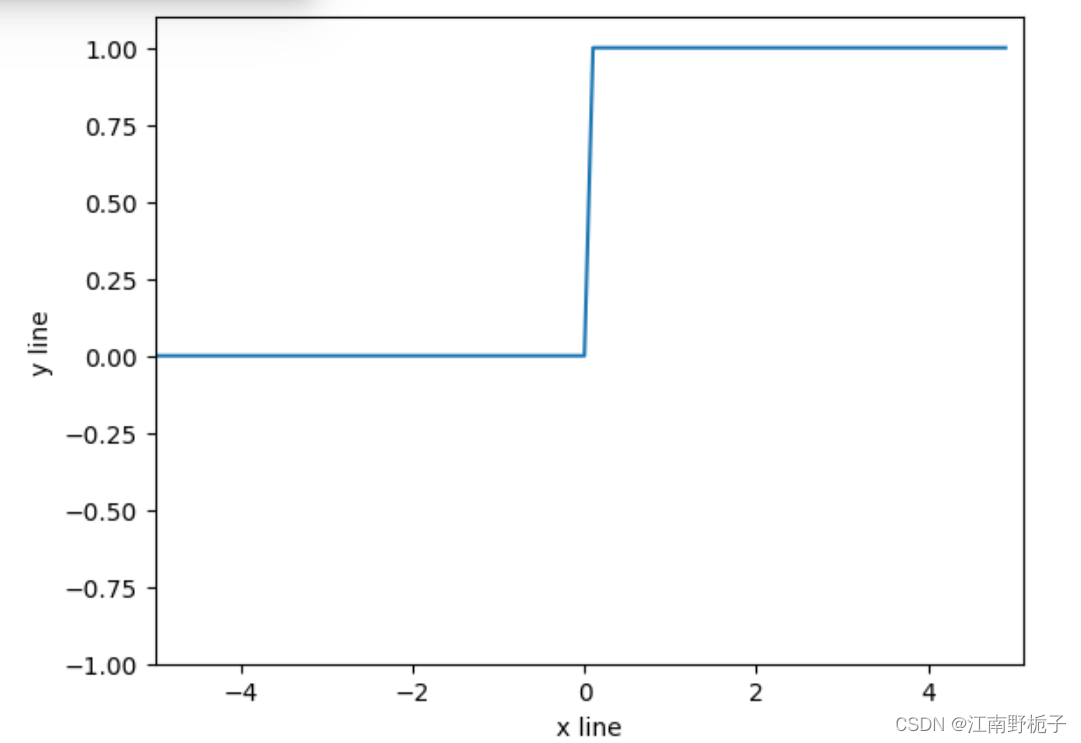
神经网络的激活函数必须使用非线性函数,如果使用线性函数,那么加深神经网络的层数就没有意义了。
2. sigmoid 函数
sigmoid 函数是一种在数学和工程领域中广泛使用的函数,在人工神经网络中也经常使用。
2.1 sigmoid 函数表达式
它的数学定义可以表示为:
其中 e 是自然对数的底数。这个函数将输入值映射到 (0,1) 的区间内,当输入值趋于正无穷或负无穷时,输出分别趋近于 1 和 0。
Sigmoid函数具有以下特性:
- 连续性和可导性:它是连续且可导的,这使得它在数学处理上非常方便。
- 有界性:函数的值域被限制在 (0,1) 之间,这个性质使得它在需要将输出解释为概率值的场景中非常有用。
- 对称性:关于原点对称,这意味着如果 x 是输入,那么 -x 也是输入,并且输出相同。
- S形曲线:它的图形呈现优美的 S 形曲线,这也是其名称的来源。
- 易于求导:它的导数可以用自身表示,即 f'(x)=f(x)(1-f(x)) ,这大大简化了计算过程。
尽管Sigmoid函数具有上述优点,但它也存在一些缺点:
- 计算量大:由于涉及指数运算,它的计算成本相对较高。
- 梯度消失问题:在反向传播过程中,当输入值很大或很小的时候,梯度会趋近于零,这会导致权重更新缓慢,影响网络的训练效率。
因此,虽然Sigmoid函数在神经网络和逻辑回归中有广泛的应用,但在处理深层网络时可能会遇到一些计算和优化上的挑战。
2.2 sigmoid 函数 Python 实现
sigmoid 函数的 python 实现如下:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
def sigmoid_function(x):return(1/(1+np.exp(-x)))
x=np.arange(-5.0,5.0,0.1)
y1=step_function(x)
y2=sigmoid_function(x)
plt.plot(x,y1,label="step")
plt.plot(x,y2,linestyle="dashdot",label="sigmoid")
plt.xlabel("x line")
plt.ylabel("y line")
plt.xlim(-5,5.1) #指定 x 轴的位置
plt.ylim(-1,2) #指定 y 轴的位置
plt.show()2.4 sigmoid 函数图
下面是 sigmoid 函数和阶跃函数的比对图。
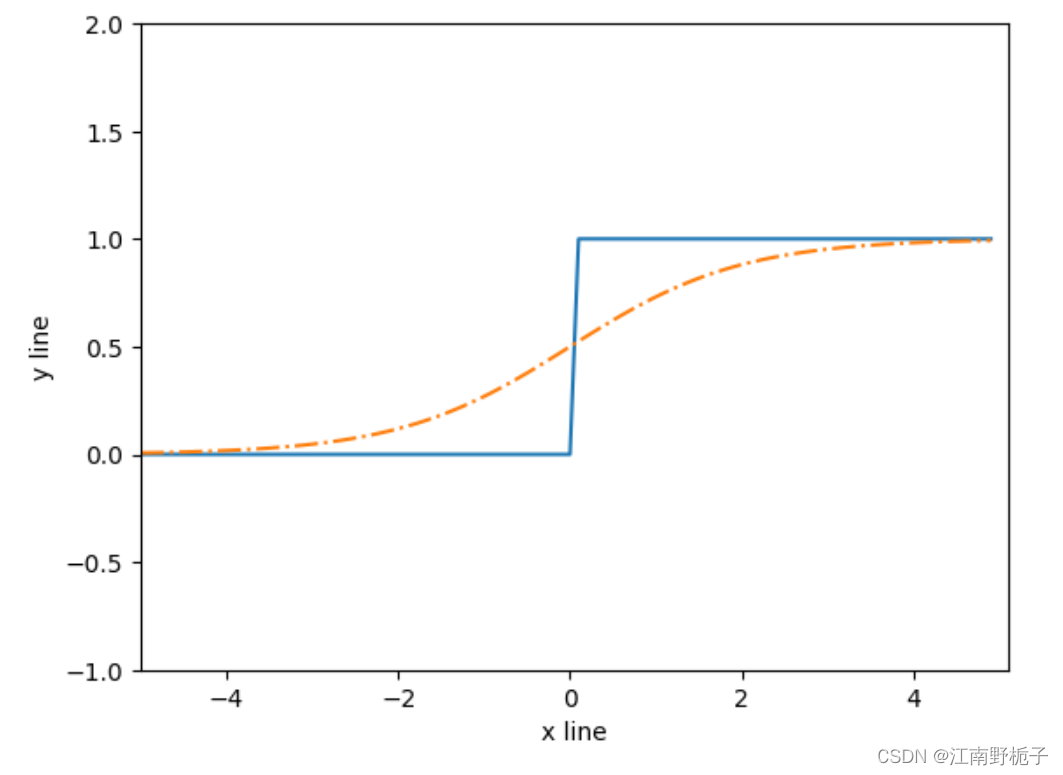
从图上看 sigmoid 函数和阶跃函数 还是有很多共同之处:
- 不管输入信号是多少,输出信号都是在 0 和 1 之间。
- 输入信号越大,输出信号越接近 1;输入信号越小,输出信号越接近 0;
3. ReLU 函数
ReLU(Rectified Linear Unit)函数是一种常用的激活函数,近些年 ReLU 函数在深度学习中被广泛应用,因为它的计算简单且能够有效地缓解梯度消失问题。
ReLU函数的优点包括:计算简单,梯度不会饱和,能够加速收敛速度,并且能够提供稀疏激活性。
3.1 ReLU 函数表达式
ReLU 函数在输入大于 0 时候,直接输出该值;在输入小于 等于 0 时候,输出 0.
其数学表达式为:
3.2 ReLU 函数 Python 实现
ReLU 函数的 python 实现如下:
def ReLU_function(x):return(np.maximum(0,x))
x=np.arange(-5.0,5.0,0.1)
y=ReLU_function(x)
plt.plot(x,y,label="ReLU")
plt.xlabel("x line")
plt.ylabel("y line")
plt.xlim(-5,5.1) #指定 x 轴的位置
plt.ylim(-5,5.1) #指定 y 轴的位置
plt.show()3.4 ReLU 函数图
下面是 sigmoid 函数、阶跃函数、ReLU 的比对图。
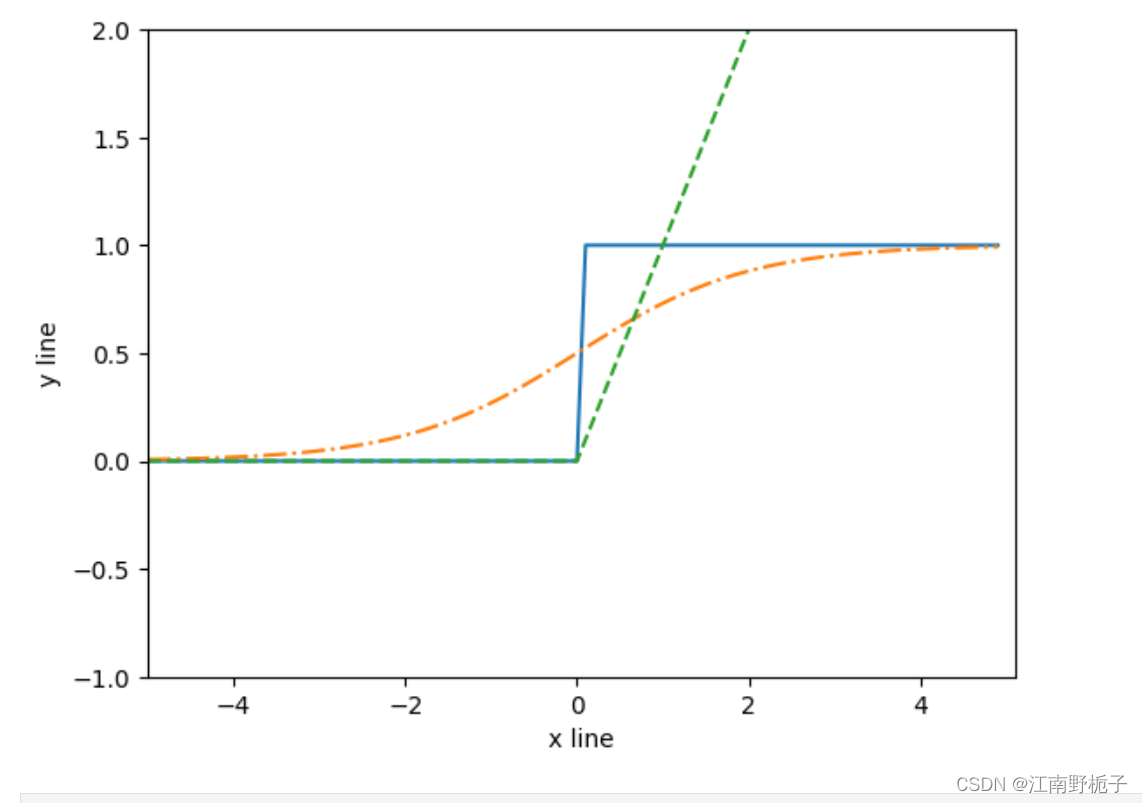
'''
要是大家觉得写得还行,麻烦点个赞或者收藏吧,想给博客涨涨人气,非常感谢!
'''