声明:文章是从本人公众号中复制而来,因此,想最新最快了解各类智能优化算法及其改进的朋友,可关注我的公众号:强盛机器学习,不定期会有很多免费代码分享~
目录
原理简介
一、初始化阶段
二、全局开发阶段
三、局部勘探阶段
(1)发射电磁波
(2)反射电磁波
(3)接收电磁波
算法伪代码
性能测评
参考文献
完整代码
波搜索算法(Wave Search Algorithm, WSA)是一种新型的元启发式算法(智能优化算法),灵感来源于雷达技术的启发,采用了新的初始化方法和边界约束规则以及各种改进的贪心机制,总体上看性能不错~作者23个标准测试函数和CEC2017上对WSA进行了测试,证明了WSA算法的优越性。该成果由Haobin Zhang等人于2024年4月发表在SCI期刊《The Journal of Supercomputing》上!

由于发表时间较短,谷歌学术上还没人引用!你先用,你就是创新!

原理简介
灵感:雷达技术是一种利用电磁波探测目标位置、速度和形状的无线通信技术。它通过发射无线电波,接收反射回波,并对回波进行处理和分析,实现对目标的检测、定位、跟踪和识别。
一、初始化阶段
首先,我们需要执行一系列初始化准备。我们设粒子数为n,待优化问题维数为d,用矩阵模拟电磁波粒子W的位置:
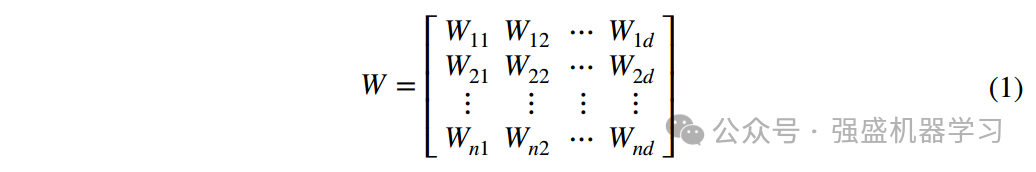
并用f ([Wn1, Wn2,⋯Wnd])表示第n个个体的适应度值,种群的适应度值可以用以下向量表示:
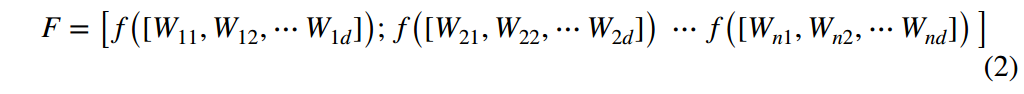
最后,准备n个随机数k1, k2......Kn从0到1,初始化粒子位置。
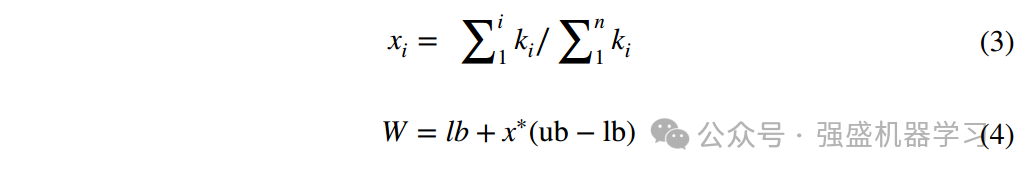
其中xi是均匀化的ki, xi*是x中的随机值,lb和ub为搜索空间的上下边界。
二、全局开发阶段
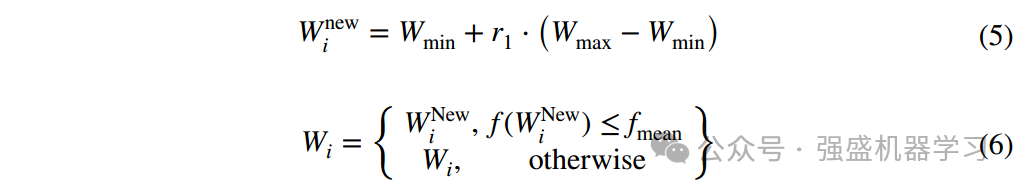
式中,Wmin是由W各维上的最小值组成的向量,Wmax是由W各维上的最大值组成的向量,fmean是所有粒子适应度值的平均值,r1是0到1之间的随机数,t是当前迭代次数,t是总迭代次数。
式(5)的好处是可以逐步缩小搜索范围,新生成的点在缩小的范围内生成,提高了搜索效率。式(6)是一种改进的贪心机制,控制种群在全局最优位置附近的位置。
三、局部勘探阶段
(1)发射电磁波
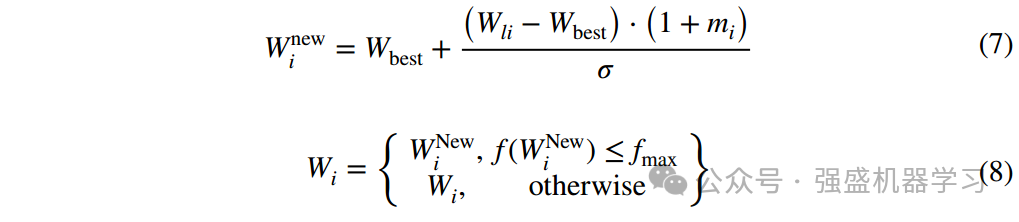
式中σ=−(5t∕T−2)/√(25(5t∕T−2)2) + 0.7,σ为波形大小控制系数,m为元素服从正态分布并按顺序排列的列向量,Wbest为当前最优位置,Wl为W按与Wbest的接近程度重新排列后的位置矩阵,fmax为群中最大的适合度值。式(7)的作用是模拟电磁波向外扩散,减少陷入局部最优的可能性,提高搜索效率。式(8)是一种改进的贪心机制,其作用是当群体位置向外波动时,使群体位置不劣于当前群体位置。
(2)反射电磁波
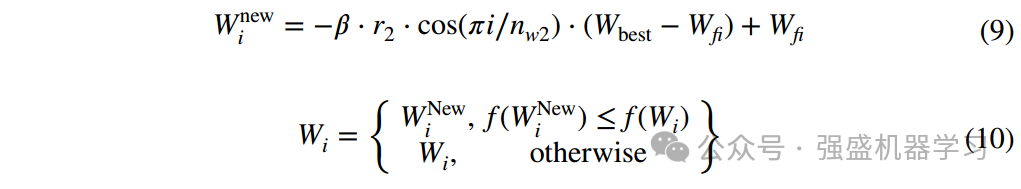
式中β= 0.75 + e−i∕nw2,β为反射强度系数,r2为0 ~ 1的随机值,nw2为模拟反射电磁波的粒子数。Wfi是W按照适应度值从小到大的顺序重新排列后的位置矩阵。式(9)模拟了部分粒子(适应度值较低的粒子)遇到障碍物向Wbest反射,而剩余粒子(适应度值较高的粒子)远离Wbest继续向外扩散。
(3)接收电磁波
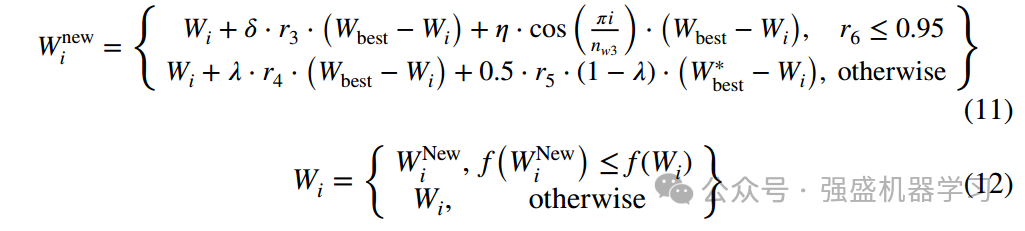
式中δ为接收系数,δ= 0.6 +(1.2−0.5)sin (tπ/2T),η为服从正态分布的随机数,nw3为模拟接收电磁波的粒子数。Wbest*是由通过卷积得到的历史最优位置,Wbest*= [Wbest1;Wbest2;Wbest3⋯Wbestt]∗([I1;I2;I3⋯It]),I1=I2= I3⋯It=1∕t。λ为校正因子,λ= (2t∕T−0.7)∕(0.78+|2t∕T−0.7|)+1。r3、r4、r5、r6是0到1的随机数。式(11)模拟了雷达通常正常接收电磁波,但有时会受到干扰,需要进行校正和处理。其作用是使粒子群体向当前最优方向搜索。同时,有一定的概率会向W方向偏转,以减少陷入局部最优的可能性。
最后,引入了一种确定性优化技术:基于中心差分法的拟合梯度下降法。其数学表达式为:
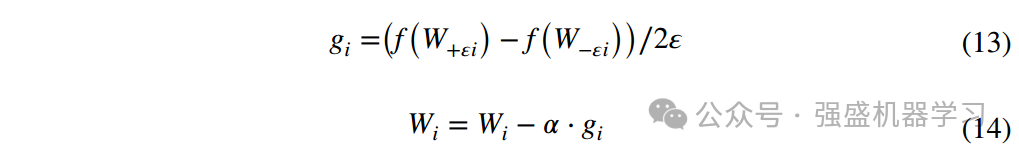
式中,W+εi = Wi +ε,W−εi = Wi−ε,ε= 10−6,g为梯度,α为步长系数,将α的初始值设为α0=0.3,通过步长试验确定最终的步长。步长试验方法如下:如果初始步长迭代后的适应度值小于等于当前适应度值,则α=α0∕c,否则α=α0*c,其中c为缩放因子。式(14)采用中心差分法拟合待优化问题的解析信息,用于搜索最优解,以提高搜索效率和精度。值得注意的是,该策略是一种确定性优化技术。WSA算法通过引入该策略,结合了确定性和不确定性优化技术。
另外,广义的边界限制规则是将越过边界的粒子放在边界上。我们发现这种方法降低了粒子群的多样性。因此,我们建议将超出边界的粒子随机设置在搜索范围内。数学表达式为:
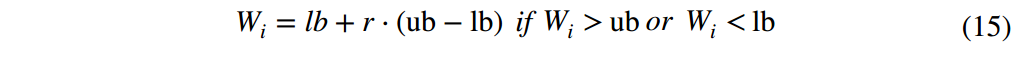
其中,lb和ub分别为搜索范围的下边界和上边界,r是一个d维随机化列向量,其元素值范围为0到1。
算法伪代码
为了使大家更好地理解,这边给出算法伪代码,非常清晰!

如果实在看不懂,不用担心,可以看下源代码,再结合上文公式理解就一目了然了!
性能测评
原文作者在经典的23个基准测试函数和30个CEC2017测试函数)对WSA算法进行测试,并将WSA算法应用于六个常见工程问题和移动机器人路径规划问题,将其与最先进和高引用算法进行比较。实验结果表明,WSA算法的优化能力优于其他最先进的优化算法,能够有效地解决实际工程问题。
这边为了方便大家对比与理解,采用23个标准测试函数,即CEC2005,并与性能较为广受认可的麻雀优化算法SSA进行对比!这边展示其中5个测试函数的图,其余十几个测试函数大家可以自行切换尝试!
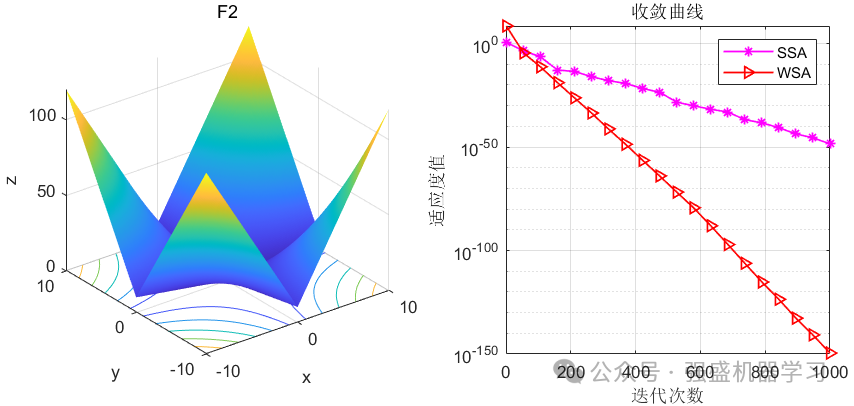
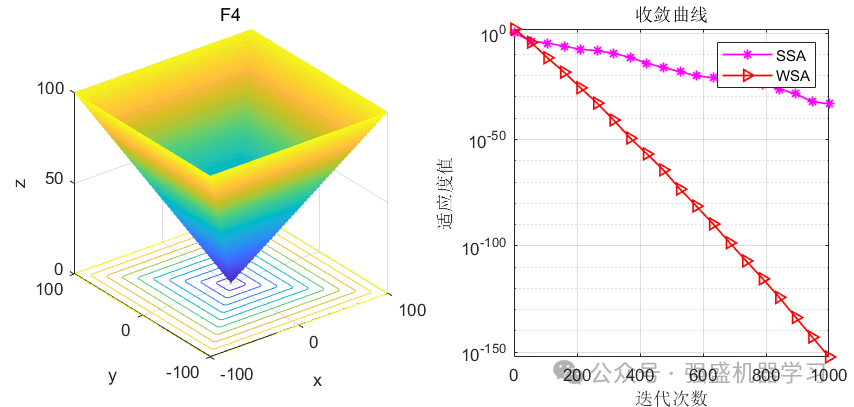
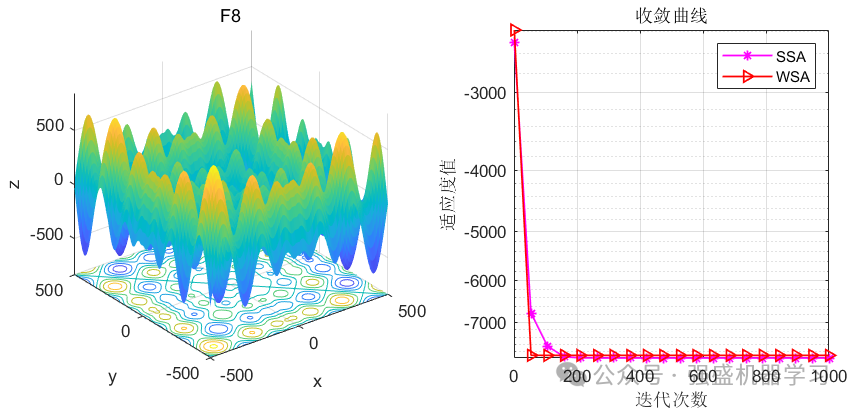
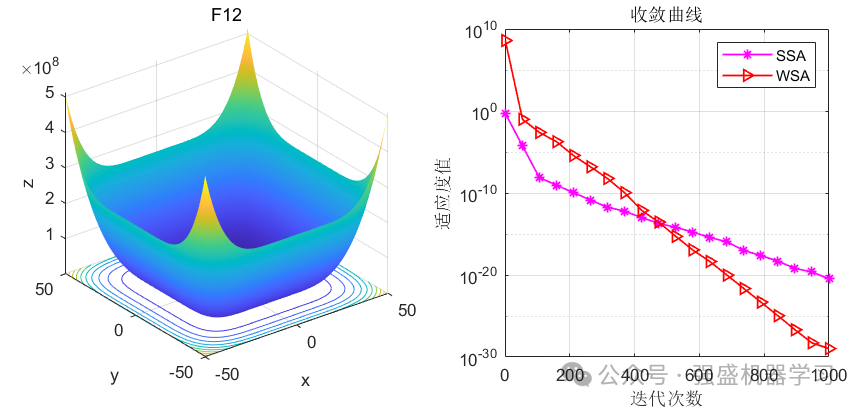
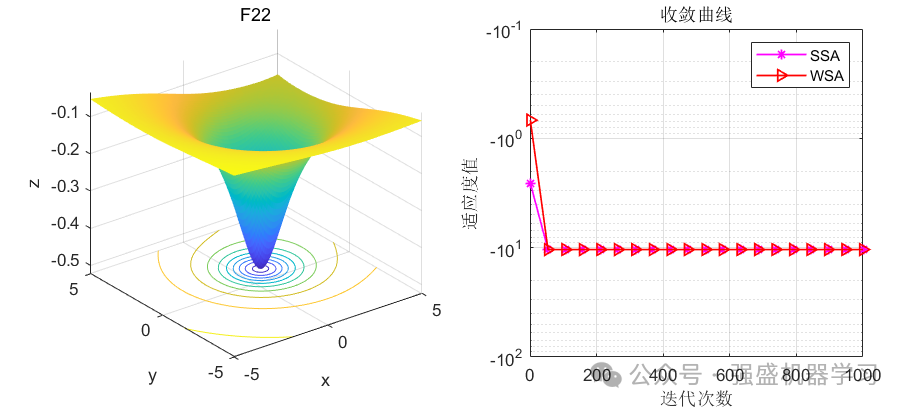
可以看到,WSA在许多高难度的函数上都超过了经典的SSA算法,表明该算法性能是非常优越的,很有说服力,大家应用到各类预测、优化问题中是一个不错的选择~
参考文献
[1]Zhang H, San H, Sun H, et al. A novel optimization method: wave search algorithm[J]. The Journal of Supercomputing, 2024: 1-36.
完整代码
如果需要免费获得图中的完整测试代码,只需点击下方小卡片,后台回复关键字:
WSA
也可点击下方小卡片,后台回复个人需求(比如WSA-SVM)定制以下青蒿素算法优化模型(看到秒回):
1.回归/时序/分类预测类:SVM、RVM、LSSVM、ELM、KELM、HKELM、DELM、RELM、DHKELM、RF、LSTM、BiLSTM、GRU、BiGRU、PNN、CNN、BP、XGBoost、TCN、BiTCN、ESN等等均可~
2.组合预测类:CNN/TCN/BiTCN/DBN/Adaboost结合SVM、RVM、ELM、LSTM、BiLSTM、GRU、BiGRU、Attention机制类等均可(可任意搭配非常新颖)~
3.分解类:EMD、EEMD、VMD、REMD、FEEMD、TVFEMD、CEEMDAN、ICEEMDAN、SVMD等分解模型均可~
4.其他:机器人路径规划、无人机三维路径规划、DBSCAN聚类、VRPTW路径优化、微电网优化、无线传感器覆盖优化、故障诊断等等均可~
5.原创改进优化算法(适合需要创新的同学):2024年的波搜索算法WSA以及麻雀SSA、蜣螂DBO等任意优化算法均可,保证测试函数效果!
更多免费代码链接:更多免费代码链接