主要内容
之前发布了非线性问题线性化的几种方法,如知识分享|分段函数线性化及matlab测试,学习园地 | yalmip实用操作-线性化,非线性优化 | 非线性问题matlab+yalmip求解案例,但是在实际建模及编程过程中,会遇到各种各样的问题,比如下面的模型就出现了非凸的报错问题,主要原因在于目标函数为两个变量乘积。

该问题直接写成matlab代码如下:
clear;clc;
% ====== 变量定义 ======%
x=sdpvar(1,2,'full');
r=sdpvar(1,2,'full');
b1=binvar(2,1,'full');
b2=binvar(2,1,'full');
% ====== 约束表达 ======%
P=[30,70];
C=[];
C=[C,x(1)+x(2)==100];
C=[C,0.5*P(1)<=x(1)<=3*P(1),0.5*P(2)<=x(2)<=3*P(2)];
C=[C,sum(b1)==1,implies(b1(1),[x(1)>=0.8*P(1),r(1)==0.0200]);implies(b1(2),[x(1)<=0.8*P(1),r(1)==0.0162])];
C=[C,sum(b2)==1,implies(b2(1),[x(2)>=0.9*P(2),r(2)==0.0195]);implies(b2(2),[x(2)<=0.9*P(2),r(2)==0.0130])];
C=[C,x(1)>=0,x(2)>=0];
% ===== 目标及求解 ======%
F=(-1)*(r(1)*x(1)+r(2)*x(2));
ops = sdpsettings('solver', 'cplex'); % gurobi mosek
sol=optimize(C,F,ops);
求解之后会出现报错,主要是由于模型非凸所致,为了更好的求解该问题,需要对模型采用其他方式进行求解。
本次讨论两种解决办法,一种是分类迭代求解,另外一种是采用BigM法进行线性化处理。
1 分类迭代求解
通过观察能够看出来,r的非线性分四种情况,因此,可以分别求解四种情况下的最优解,然后通过比较确定最终最佳方案,代码如下:
clear all;clc;
P=[30,70];
Fc=200;
for i=1:4% ====== 变量定义 ======%x=sdpvar(1,2,'full');
% r=sdpvar(2);% ====== 约束表达 ======%C=[];if i==1r(1)=0.0200;r(2)=0.0195;C=[C,x(1)>=0.8*P(1),x(2)>=0.9*P(2)];elseif i==2r(1)=0.0200;r(2)=0.0130;C=[C,x(1)>=0.8*P(1),x(2)<=0.9*P(2)];elseif i==3r(1)=0.0162;r(2)=0.0195;C=[C,x(1)<=0.8*P(1),x(2)>=0.9*P(2)];elser(1)=0.0162;r(2)=0.0130;C=[C,x(1)<=0.8*P(1),x(2)<=0.9*P(2)];end
C=[C,x(1)+x(2)==100];
C=[C,0.5*P(1)<=x(1)<=3*P(1),0.5*P(2)<=x(2)<=3*P(2)];
C=[C,x(1)>=0,x(2)>=0];
% ===== 目标及求解 ======%
F=(-1)*(r(1)*x(1)+r(2)*x(2));
ops = sdpsettings('solver', 'cplex'); % gurobi mosek
sol=optimize(C,F,ops);
% ===== 判别最佳结果 ======%
F1=value(F);
x1=value(x);
r1=value(r);
if Fc>F1Fc=F1;xc=x1;rc=r1;
end
yalmip('clear');
end
最终得到的F最优值为-1.9685,x为37和63。
2.BigM法非线性处理
因为该问题的目标是两个变量乘积项导致的非线性问题,可以通过线性化方式进行转化:
令

则关于v1的约束可以转化为如下形式:
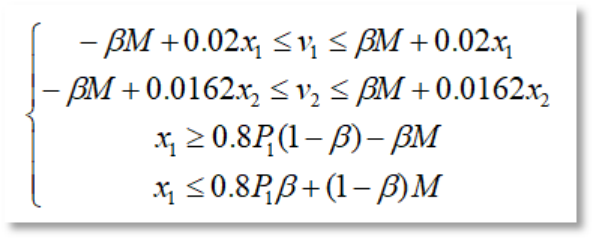
同理,关于v2的约束也可转换为上述形式。
具体代码如下:
clear;clc;
% ====== 变量定义 ======%
x=sdpvar(1,2,'full');
r=sdpvar(1,2,'full');
beta=binvar(1,2,'full');
v=sdpvar(1,2,'full');
b1=binvar(2,1,'full');
b2=binvar(2,1,'full');
% ====== 约束表达 ======%
P=[30,70];
M=100;
C=[];
C=[C,x(1)+x(2)==100];
C=[C,0.5*P(1)<=x(1)<=3*P(1),0.5*P(2)<=x(2)<=3*P(2)];
C=[C,-beta(1)*M+0.02*x(1)<=v(1)<=beta(1)*M+0.02*x(1)];
C=[C,-(1-beta(1))*M+0.0162*x(1)<=v(1)<=(1-beta(1))*M+0.0162*x(1)];
C=[C,x(1)>=0.8*P(1)*(1-beta(1))-beta(1)*M];
C=[C,x(1)<=0.8*P(1)*beta(1)+(1-beta(1))*M];
C=[C,-beta(2)*M+0.0195*x(2)<=v(2)<=beta(2)*M+0.0195*x(2)];
C=[C,-(1-beta(2))*M+0.013*x(2)<=v(2)<=(1-beta(2))*M+0.013*x(2)];
C=[C,x(2)>=0.9*P(2)*(1-beta(2))-beta(2)*M];
C=[C,x(2)<=0.9*P(2)*beta(2)+(1-beta(2))*M];
C=[C,x(1)>=0,x(2)>=0];
% ===== 目标及求解 ======%
F=-sum(v);
ops = sdpsettings('solver', 'cplex'); % gurobi mosek
sol=optimize(C,F,ops);
最终得到的F最优值为-1.9685,x为37和63,和分类迭代得到的结果是一致的。