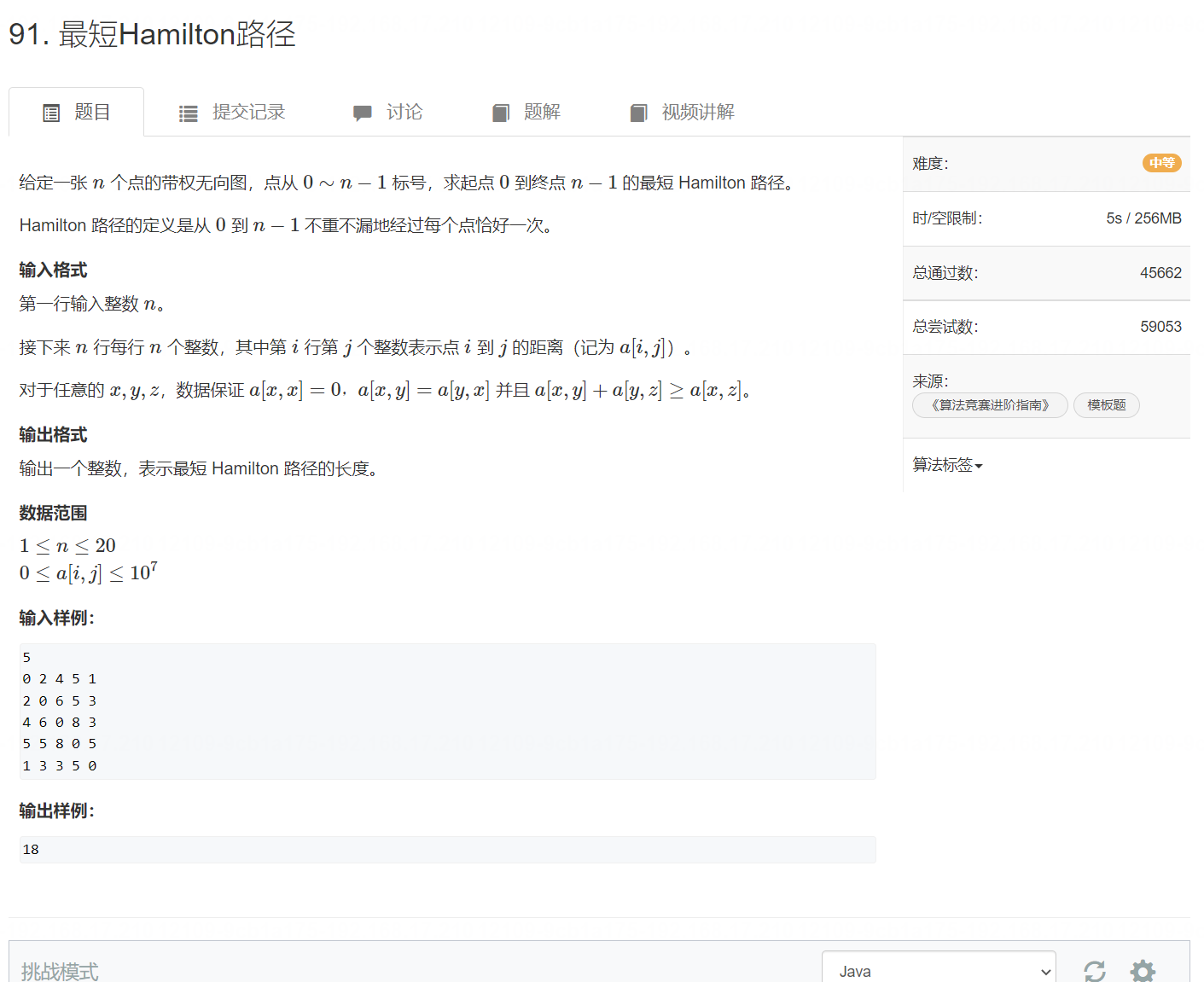
题意：
从0开始，必须走完全部节点，且不重复走，不漏走的最短距离

关键思路：

1. 从0开始 走到j 节点所走情况是 state【state表示经过的点，不代表顺序，就表示经过的点】

f[i][j]表示 从0开始 走到j 节点所走节点表示是 i

i表示的是 从0走到j 所经过的节点【用二进制表示】【没有顺序】

那么f[i][j] = 遍历i情况下的所有节点，走到j节点所用的最小值

import java.util.*;
public class Main{public static void main(String[] args){Scanner scan = new Scanner(System.in);int N = 20,M = 1 << N;int[][] f = new int[M][N];//当前的状态是i，然后走到了点j上面int[][] w = new int[N][N];int n = scan.nextInt();for(int i = 0 ; i < n ; i ++ )for(int j = 0 ; j < n ; j ++ )  w[i][j] = scan.nextInt(); // 输入每一步的权重for(int i = 0 ; i < 1 << n ; i ++ )Arrays.fill(f[i],0x3f3f3f); //除了第一个点，其他点初始化成正无穷f[1][0] = 0;for (int i = 1; i < 1 << n; i++) {for (int j = 1; j < n; j++) {// f[i][j]if ((i >> j & 1 ) == 1) {int jAfter = i - (1 << j);for (int k = 0; k < n; k++) {if (((jAfter >> k) & 1) == 1) {f[i][j] = Math.min(f[i][j],f[jAfter][k] + w[k][j]);   }}}}}//最后输出从定义出发，不难想到，f[state][j],state表示的是二进制的全0表示都走过，j表示从0走到n-1System.out.println(f[(1 << n) - 1][n - 1]);}
}