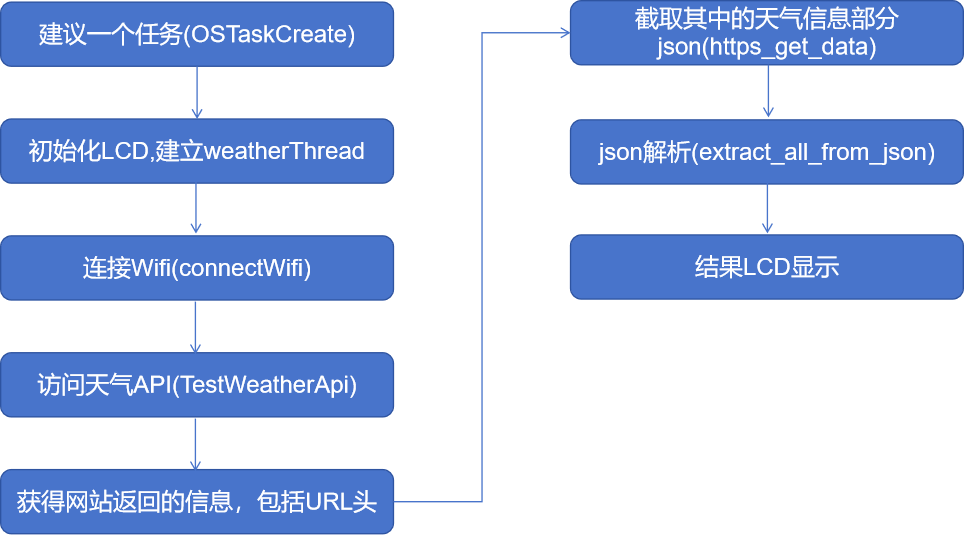
目的:求出我们的f(X),它代表着我们X映射到多维的情况,能够帮我们在多维中招到超平面进行分类。
1.优化问题:
1.1推荐好书:

1.2 优化理论中的原问题:
原问题和限制条件如下:
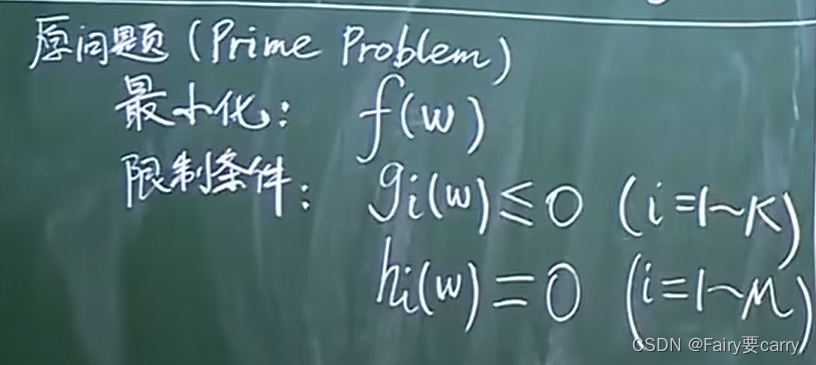
这是一个泛化性非常强的条件,为什么?
因为,我们在f函数前面加-就等于它的最大化了,包括限制条件也是,普适性非常强
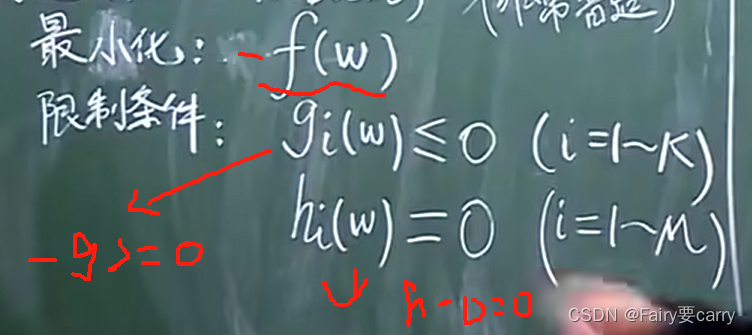
1.3我们将原问题对应到对偶问题:
首先定义一个函数L:(本质上就是一个拉格朗日乘数,目的是在一些限制条件下求出极值)。
然后明确变量:w,α,β 三种。
α向量:跟我们原问题中的gi(w)维度一样,i属于1~N,那么α属于N维向量。
β向量:跟原问题中的hi(w)维度一样,属于N维向量。
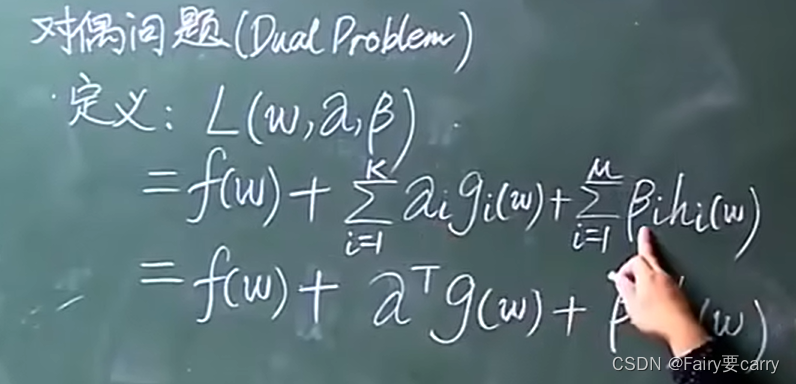
1.4 接下来就是对偶问题的定义:
inf: 求里面那个括号的最小值。
具体操作: 在限定α,β的条件下(每确定一个α和β),遍历所有的w求得最小值,然后再根据外面的α和β求得θ的最大值。
限定条件: α的每一个分量>=0
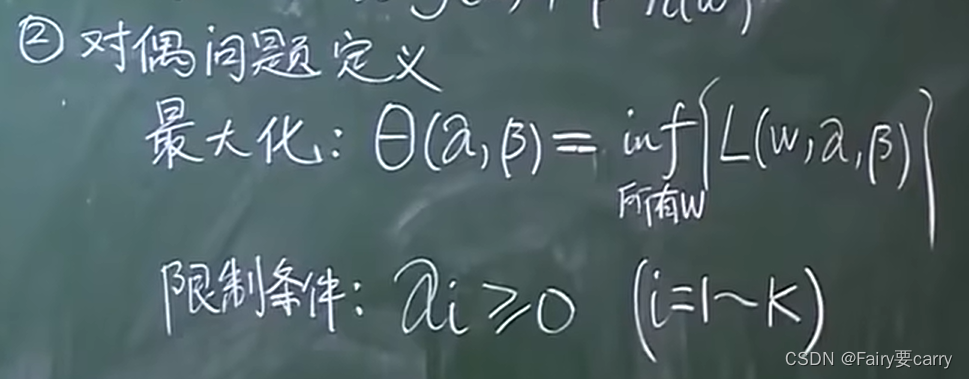
1.5 对偶问题和原问题的关系:
目的:

提供下界保证:

根据以下的w如果是原问题的解,【原问题的解(也就是上述的极小值)】,a和β*为对偶问题的解。
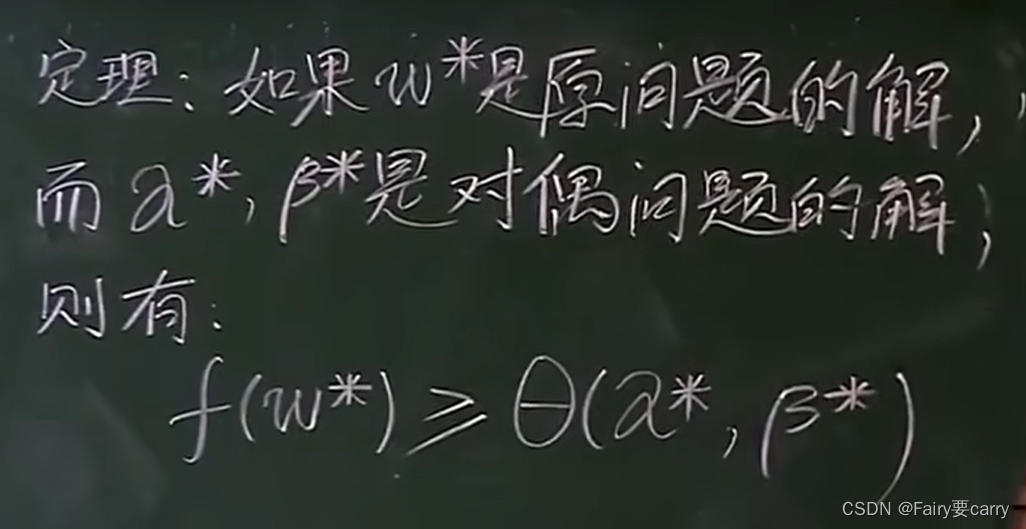
证明原问题和对偶问题的关系:
首先明确f(w*)中的w为原问题中的解,f为原问题。
其次既然w满足原问题中的解,那么限制条件就满足。
然后我们将带入w的原问题的限制条件带入对偶问题的公式中则有:
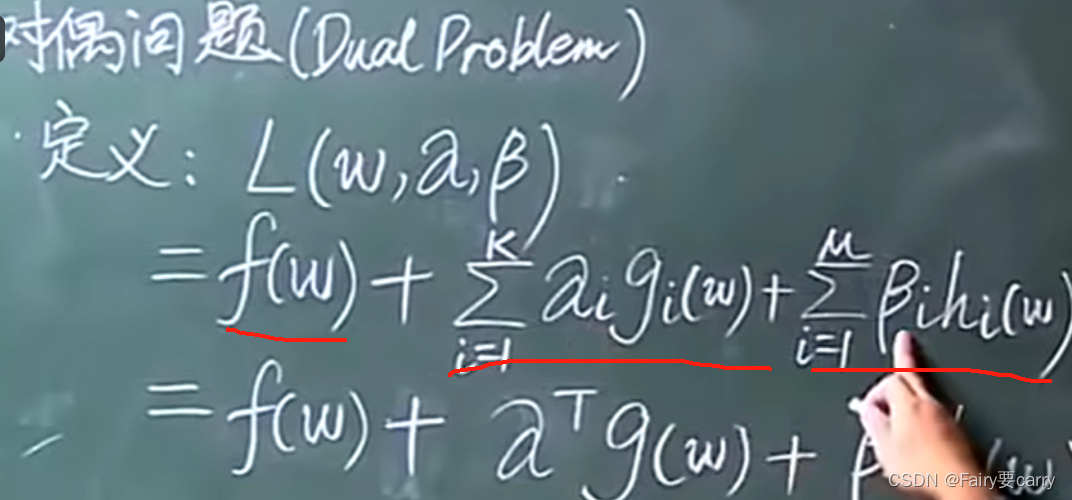
gi(w)为原问题中的限制条件,>=0.
hi(w*)为原问题中的限制条件,=0.
最后将对偶问题的限制条件αi,>=0.得出结果:
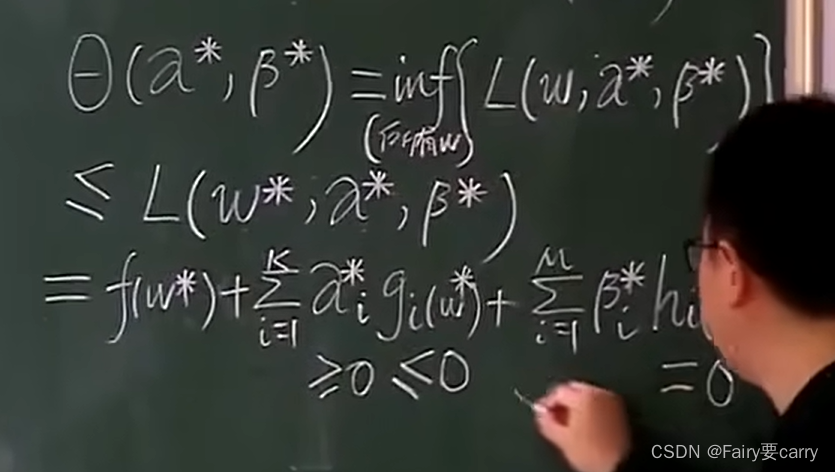
G:原问题和对偶问题的间距(本质上也是证明了原问题和对偶问题之间的关系)
在一些特定的情况下,G=0,原问题=对偶问题(也就是我们的强对偶定理)
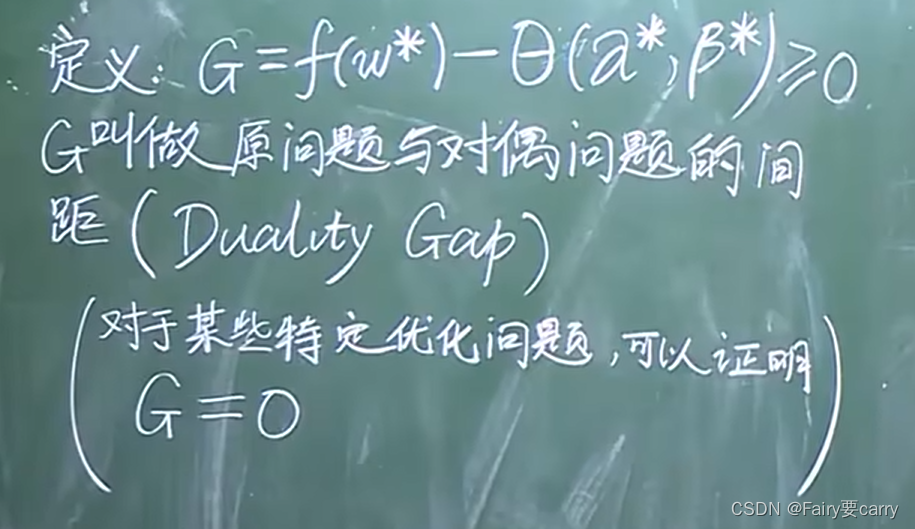
1.6 由原问题和对偶问题的关系衍生到强对偶定理:

这样意味着什么呢? 说明对偶问题的解就是原问题的解,在公式上的结论如下:

说明αi或者gi必定等于0(这也就是KKT条件,解决强对偶问题的条件)

演化为强对偶问题后,我们就能利用对偶问题去处理原问题的解。
2.如何将原问题化解为对偶问题
2.1 首先是明确定义:
首先,我们利用强对偶问题解决原问题,前提条件是原问题函数是一个凸函数。
然后明确定义,原问题f(w):求最大d那个。
其次是限制条件:对样本进行分类【yi(标签值)[权重向量通过函数映射到高维的X]+偏置】。
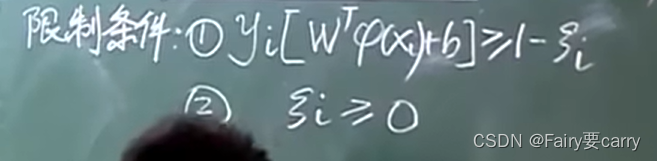
2.2 为什么原问题的函数一定要凸函数?
因为我们通过凸函数能够得到一个唯一的极值!【结论】,我们利用数学的方式给予证明【过程】:

我们将一个关于凸函数几何的问题转换成一个多维问题的解释【代数形式的定义】:

2.3 如何减少偏差?
目的:对比原题的最小化和约束条件,我们需要修改为标准形式。
1、首先得到减少误差后的对偶函数限制条件: 我们将左边的 gi(w) 转变为右侧的两条限制条件。
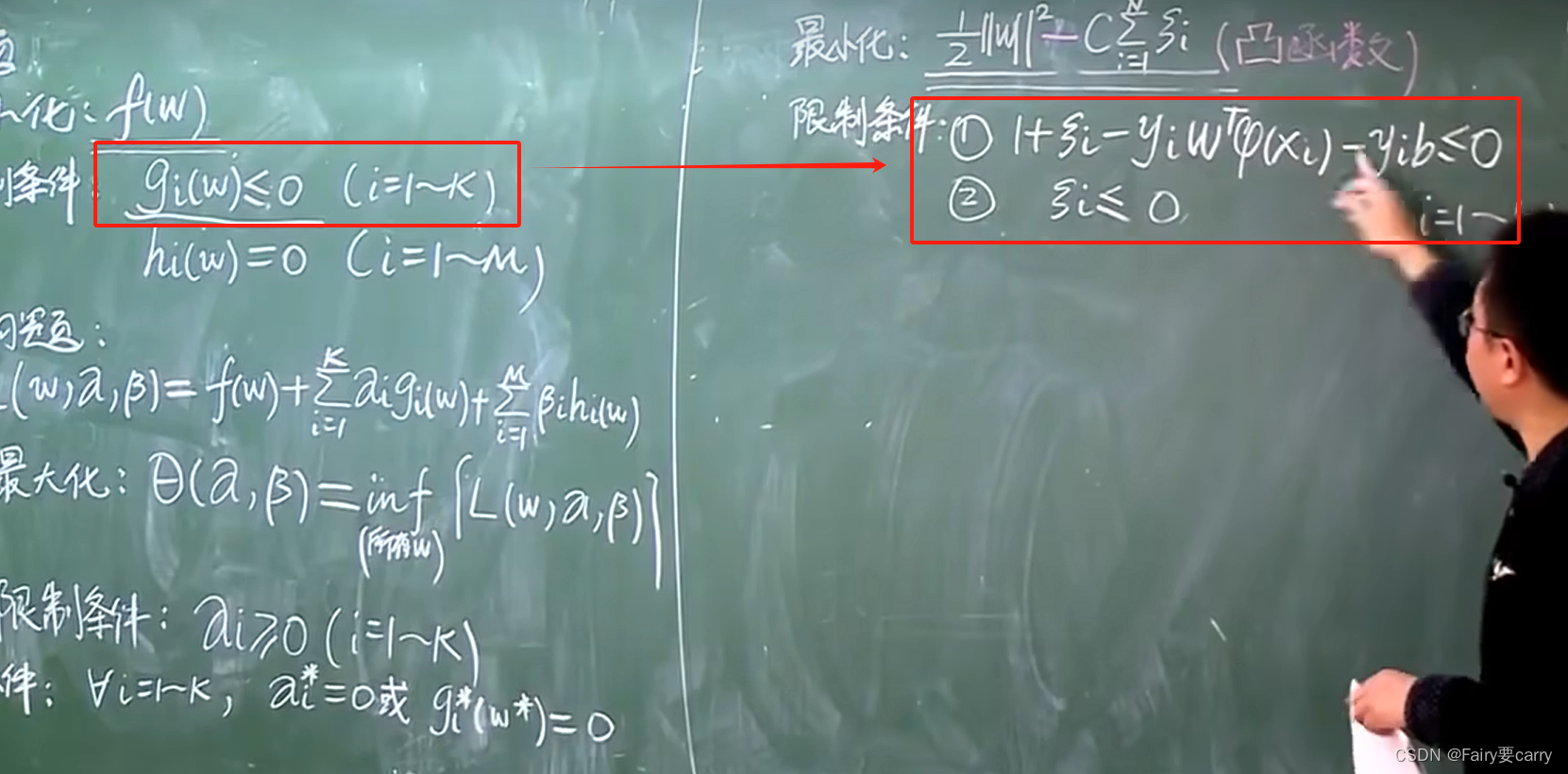
**2、然后是对偶问题的转化:**我们带入对偶问题函数 L(w),将 w 转换为 w,α,β参数带入得:
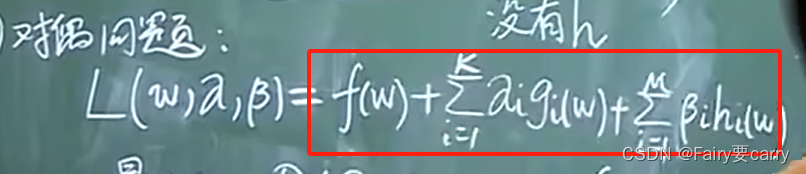
3、在减少误差环境下的新对偶函数:

4、如何减少对偶问题的函数:
我们需要寻找到能得到使L最小化结果的参数 w,γ,b
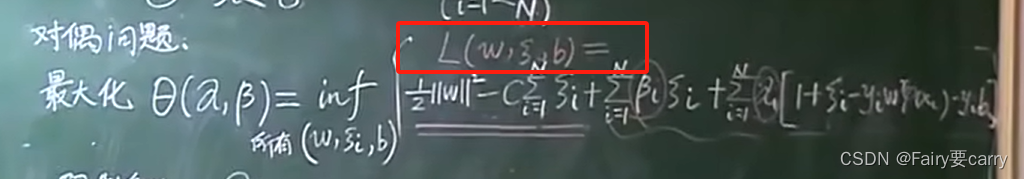
考研的知道,多元函数求极值【对变量求偏导令其为0即可求解】:

然后我们将求偏导的式子代入回原式的 θ(α,β) 函数中,得:

发现我们用对偶问题不知不觉消掉了函数:

最后得到结论θ(α,β):
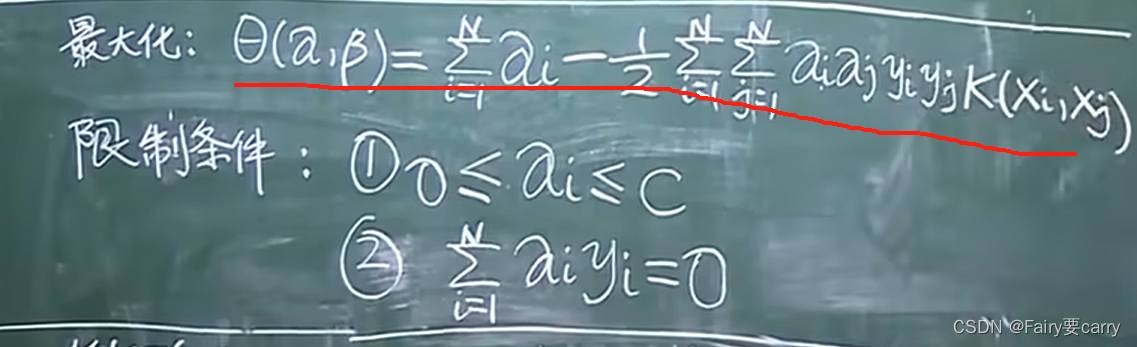
5.限制条件为什么是这个?
结合之前的对偶函数限制条件:
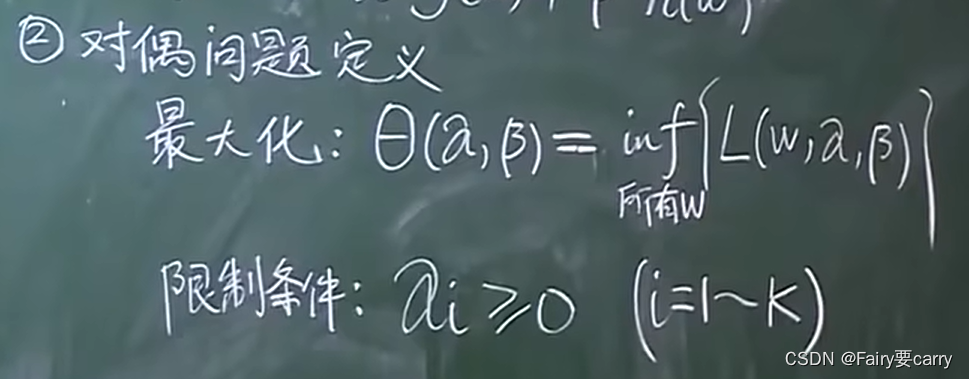
和之前推导减少误差后的θ函数公式的过程可得:
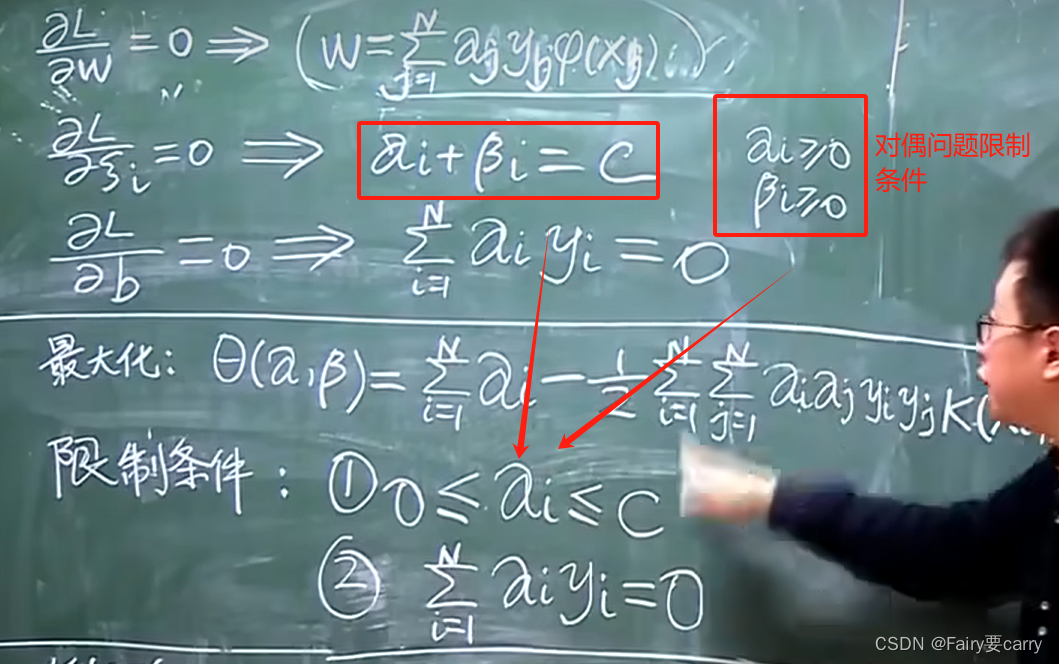
6.明确新函数的未知与已知:
kernel核函数都给定了,而α是未知变量

3.回到我们之前的测试流程求参数:
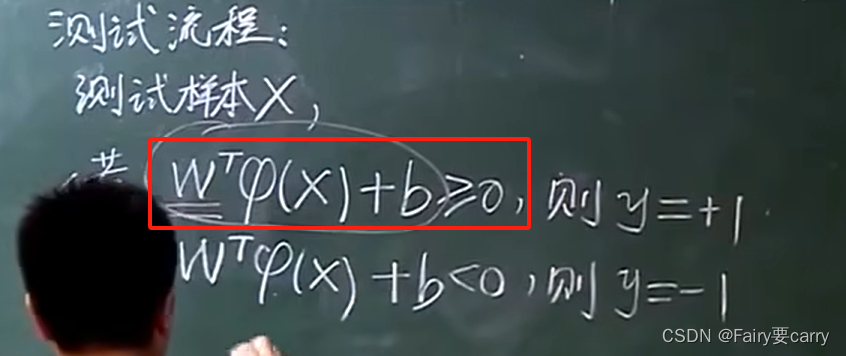
我们只要知道整个整体的情况,就 不需要知道单个升维函数,如下图所示,我们直接将W的转置代入如上测试函数中,得:
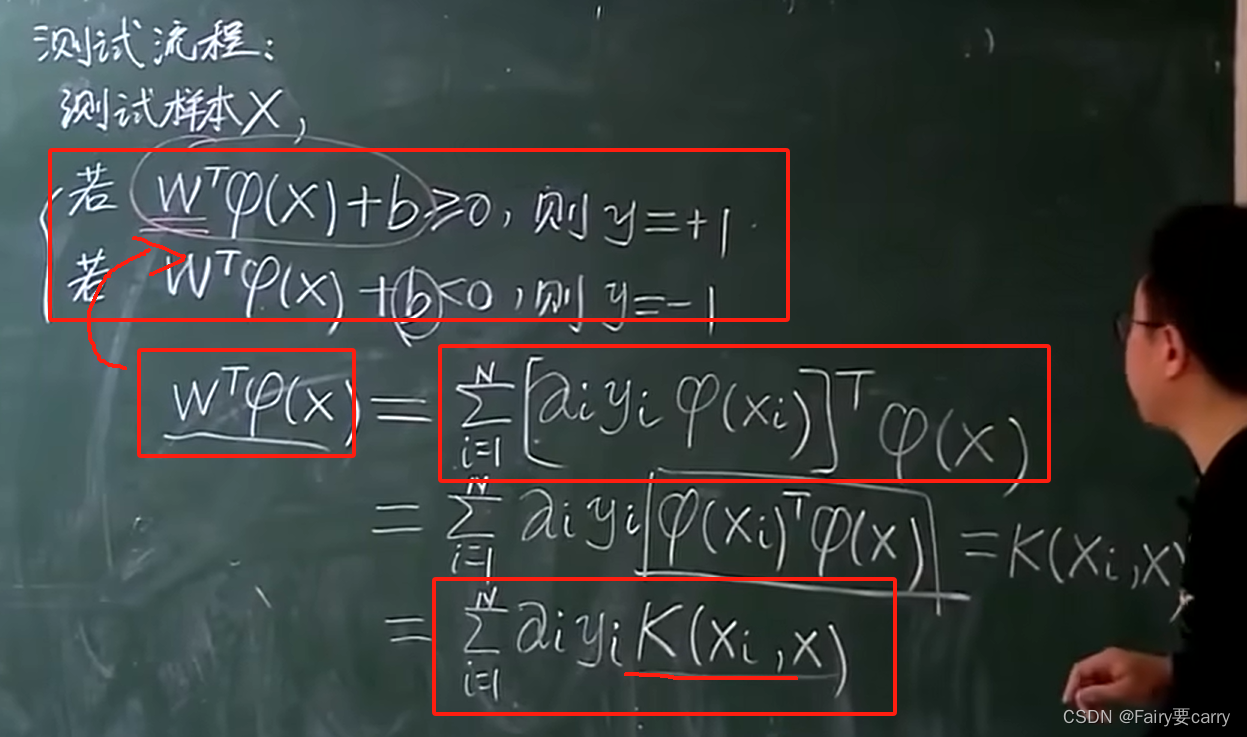
可以发现,我们无需函数,只要kernel核函数即可。这样我们的WT9(x)函数就出来了。
那么如何求b?
我们可以把所有αi(不等于0和C的)带入b的式子中求b,得到所有b的值后,然后求b的平均值。
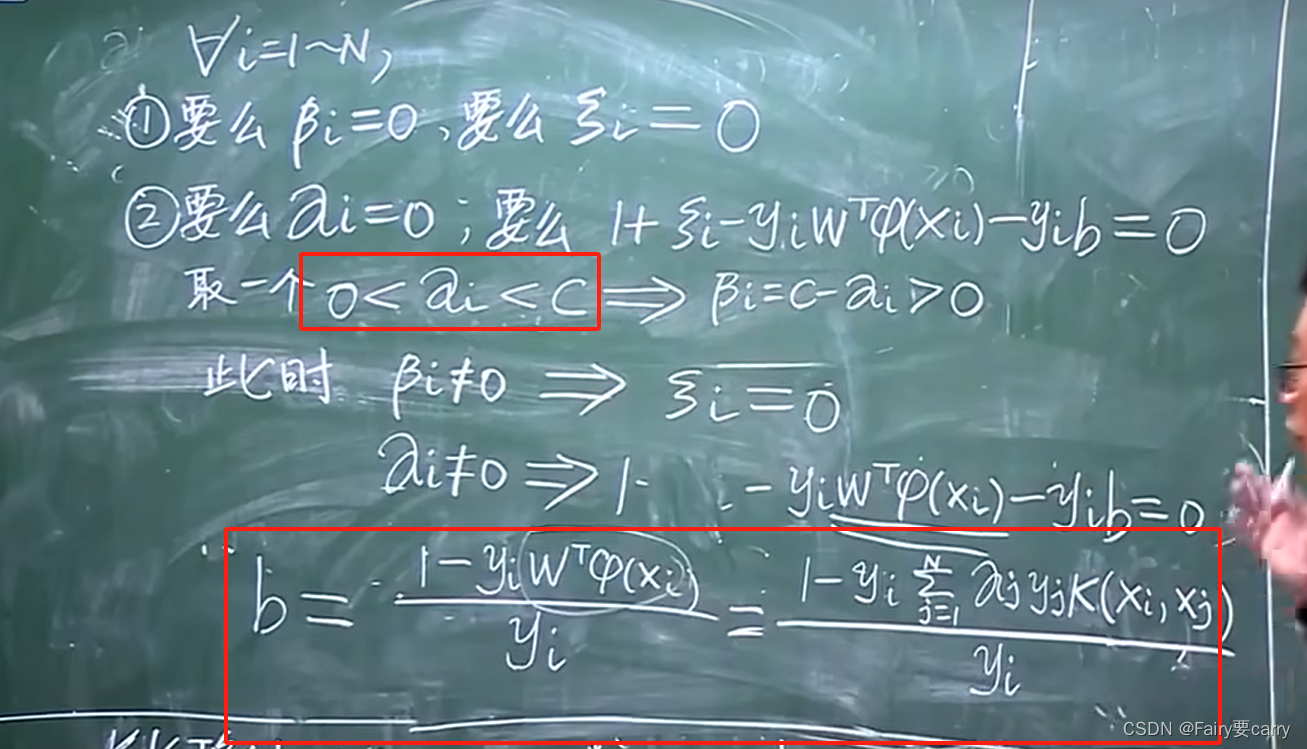
4.总结
1. 训练流程:
1.输入训练数据
2.求的 θ(α) 函数(SMO函数进行求解)
3.算 b
会发现整个训练流程只出现了Kernel而没有那个升维函数。——> 把无限维的fai函数变成有限的计算