更多资源请关注纽扣编程微信公众号

1 2019 CSP-J 阅读程序1

(程序输入不超过数组或字符串定义的范围；判断题正确填√,错误填×；除特殊说明外，判断题1.5分，选择题3分，共计40分)

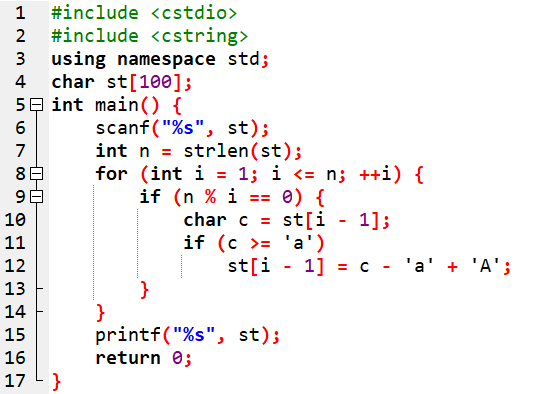
1 输入的字符串只能由小写字母或大写字母组成。（ F ）[1.5分]

2 若将第8行的“i = 1”改为“i = 0”，程序运行时会发生错误。（ T ）[1.5分]

3 若将第8行的“i <= n”改为“i * i <= n”，程序运行结果不会改变。（ F ）[1.5分]

4 若输入的字符串全部由大写字母组成，那么输出的字符串就跟输入的字符串一样。（ T ）[1.5分]

5 若输入的字符串长度为18,那么输入的字符串跟输出的字符串相比，至多有（ B ）个字符不同。[3分]

A. 18 B. 6 C. 10 D. 1

6 若输入的字符串长度为（ B ），那么输入的字符串跟输出的字符串相比，至多有36个字符不同[3分]

A. 36 B. 100000 C. 1 D. 128

2 相关知识点

1) 字符数组

函数 strlen()

作用为计算一个字符串(字符数组)中元素的个数，即从数组头部计数，直到遇到字符串结束符\0为止，计数结果不包括\0

#include<bits/stdc++.h>
using namespace std;int main(){char c[]={'a','b','c','d'};//字符数组中有4个元素 cout<<"字符数组中元素个数: "<<strlen(c);//strlen返回字符串(字符数组)中元素的个数 return 0;
}

2) 唯一分解定理

唯一分解定理又称为算术基本定理，其性质是每个大于1的自然数N（非质数）均可以被分解且他们的分解形式是唯一的

任何一个大于1的自然数 N，如果N不为质数，那么N可以唯一分解成有限个质数的乘积N=P1^a1 * P2^a2 * P3^a3 … Pn^an，这里P1<P2<P3…<Pn均为质数，其中指数ai是正整数。这样的分解称为 N 的标准分解式

例如

18 = 2^1 * 3^2

3) 约数

约数，又称因数。整数a除以整数b(b≠0) 除得的商正好是整数而没有余数，我们就说a能被b整除，或b能整除a。a称为b的倍数，b称为a的约数。

例如

6的正约数有：1、2、3、6

10的正约数有：1、2、5、10

3) 求某数约数的个数

例如18的约数有几个？

根据唯一分解定理 18 = 2^1 * 3^2

可知 约数是有2和3这2个素数组成，

第1步

2可以是0个2，1个2这2种

第2步

3可以是0个3，1个3，2个3这3种

根据乘法原理 2 * 3 = 6种，分别是1 2 3 6 9 18 这6个数字

3 思路分析

1 输入的字符串只能由小写字母或大写字母组成。（ F ）[1.5分]

分析

字符串输入不仅仅可以输入大小写字母，还可以数字，特殊字符等键盘上可输入的字符

2 若将第8行的“i = 1”改为“i = 0”，程序运行时会发生错误。（ T ）[1.5分]

分析

如果i可以为0的话，n%i取余中i不能为0，i为0将会导致运行时错误或异常

如果i可以为0的话，st[i-1]=st[-1] ,数组下标从0开始，不能为-1

3 若将第8行的“i <= n”改为“i * i <= n”，程序运行结果不会改变。（ F ）[1.5分]

分析

如果改成i * i <= n将提前退出循环

本来是把数组中所有字符检查是小写字母的变成大写字母，现在只能从开始到sqrt(n)这个些位置的的小写字母变成大写字母了

4 若输入的字符串全部由大写字母组成，那么输出的字符串就跟输入的字符串一样。（ T ）[1.5分]

分析

本程序的主要功能是把数组中所有字符检查是小写字母的变成大写字母，如果本来就是大写字母，则不用替换，和原来字符一样

5 若输入的字符串长度为18,那么输入的字符串跟输出的字符串相比，至多有（ B ）个字符不同。[3分]

A. 18 B. 6 C. 10 D. 1

分析

只有小写字母可能不同，i从1开始，所有满足字符长度n%i==0的情况都是小写字母时，不同的最多

字符长度是18，满足条件的有1 2 3 6 9 18 中的6个数

6 若输入的字符串长度为（ B ），那么输入的字符串跟输出的字符串相比，至多有36个字符不同[3分]

A. 36 B. 100000 C. 1 D. 128

分析

只有小写字母可能不同，i从1开始，所有满足字符长度n%i==0的情况都是小写字母时，不同的最多

这些数正好是n的约数

A 中36 =2^2 * 3^2 ，

第1步，2的取法：2可以取0个，2取1个，2取2个，总共3种情况

第2步，3的取法：3可以取0个，3取1个，3取2个，总共3种情况

根据乘法原理 3 * 3 = 9 种 (1,2,3,4,6,9,12,18,36)

B 100000=2^5 * 5^5

第1步，2的取法: 2可以取0个，2取1个…,2取5个，总共6种情况

第2步，5的取法: 5可以取0个，5取1个…,5取5个，总共6种情况

根据乘法原理 6 * 6 = 36 种

C 1种

D 中 128 =2^7

2的取法有，0个2，1个2，2个2，…7个2 共有8种(1,2,4,8,16,32,64,128)