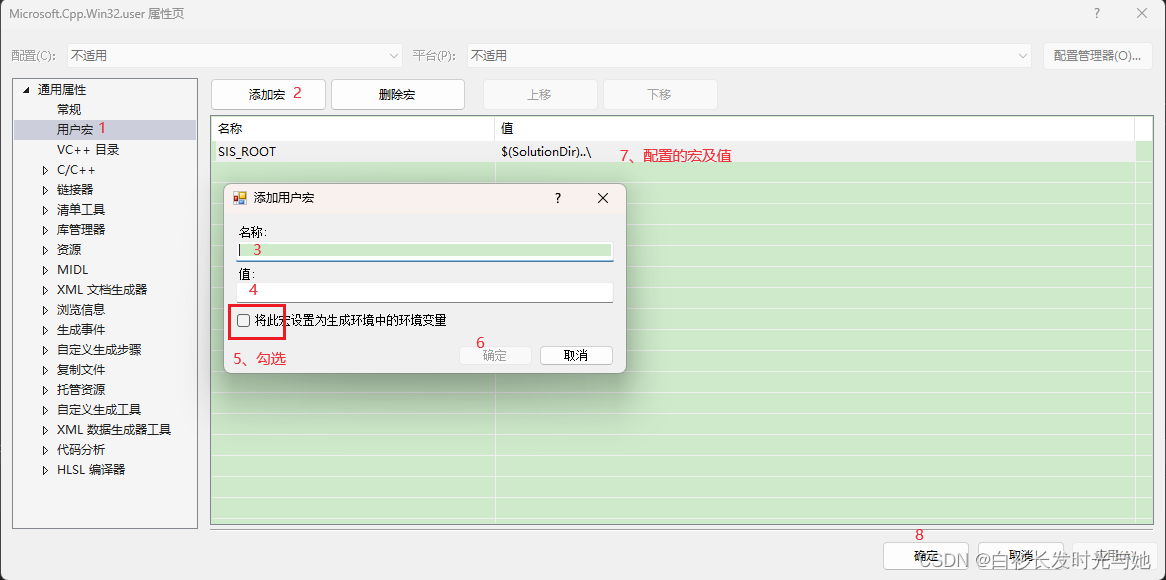
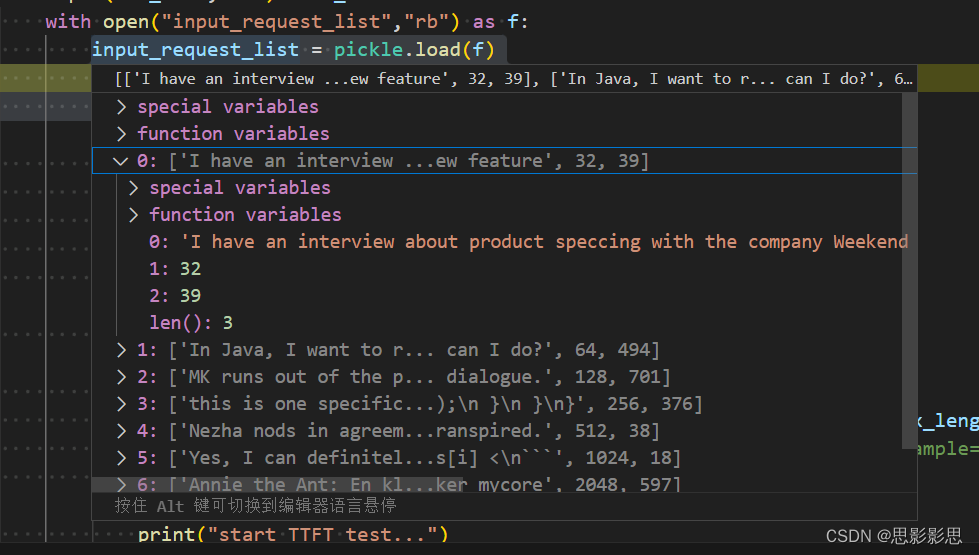
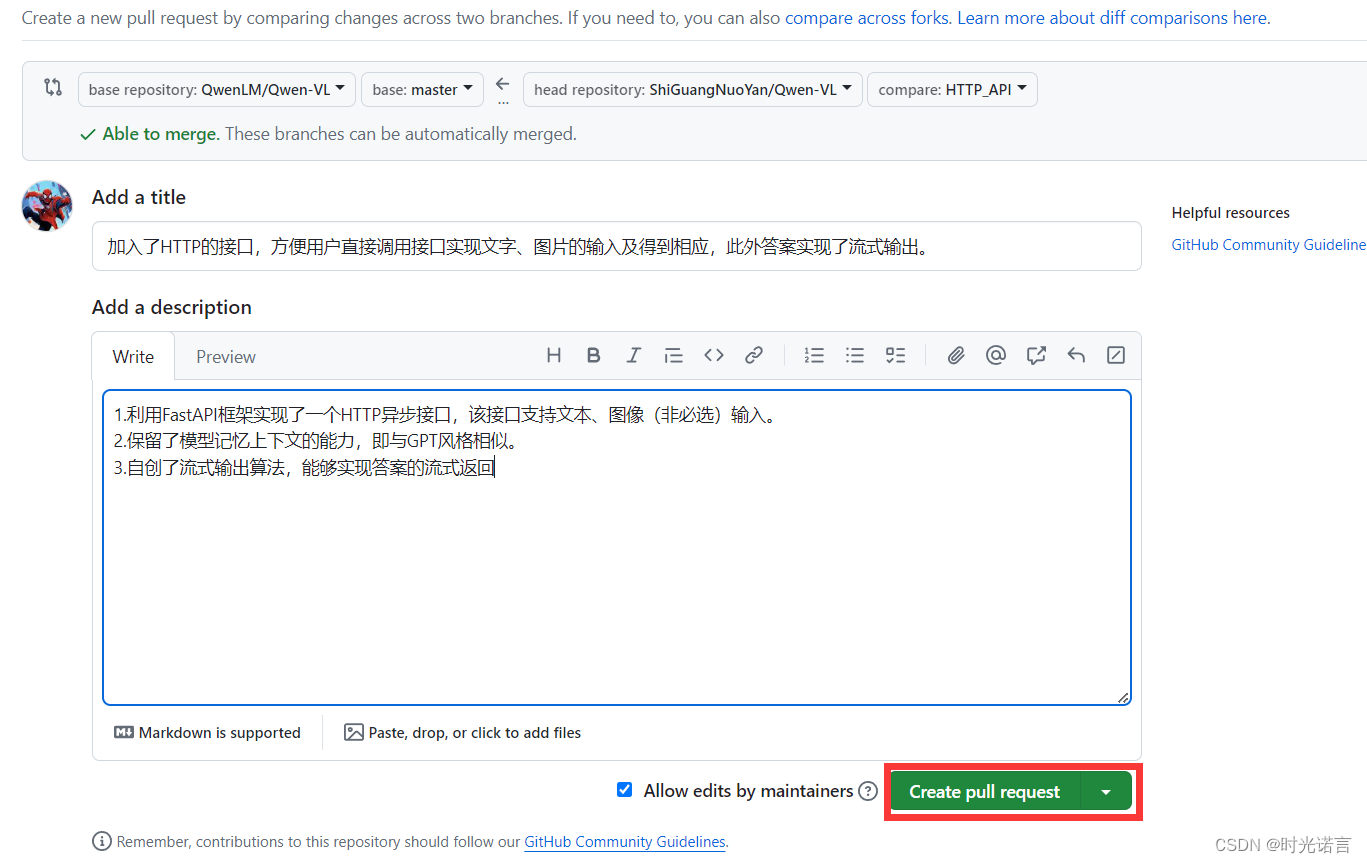
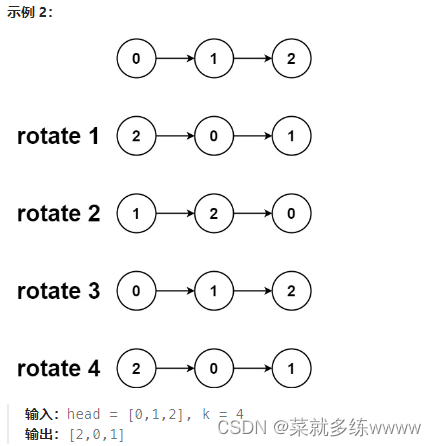
WAF简介
WAF的具体作用就是检测web应用中特定的应用,针对web应用的漏洞进行安全防护,阻止如SQL注入,XSS,跨脚本网站攻击等
正向代理
WAF和客户端与网络资源服务器都建立连接,但是WAF 的工作口具有自己的 IP 地址,客户端实际是与 WAF 建立 TCP 连接,再由 WAF 使用自己的 IP 与服务器建立请求关系
反向代理
反向代理 WAF 的工作口具有自己的 IP 地址,客户端实际是与 WAF 建立 TCP 连接,再由 WAF 使用自己的 IP 与服务器建立请求关系,其特点是真实的服务器隐藏在 WAF 后面,客户端对服务器的访问强依赖 WAF 的代理,客户端不知道具体是那台服务器。这样的架构可以使 WAF 作为中间人很容易地进行 HTTP 及 HTTPS 防护,网络的负载均衡,黑客无法攻击到真正的服务器,制作缓存
透明代理
透明代理(Transparent Proxy)也是一种代理技术,其不具有自己的 IP,客户端发起请求的目的 IP 就是服务器 IP。透明代理 WAF 一般串联在客户端与服务器之间,分别用服务器 IP 与客户端建立连接,用客户端 IP 与服务器连接,以达到“两头骗”的目的。
其中实线代表着真实的 TCP 连接,虚线代表着从客户端和服务器的角度看到的网络连接。由于它是一种劫持代理技术,所以这种部署方式从物理拓扑上要求代理网关会接收到客户端与服务器通信的所有内容,否则会出现一端 TCP 收包不全而发生连接超时现象。
透明桥代理
透明桥(Transparent Bridge)部署的拓扑位置与透明代理类似,也是串联在客户端与服务器的必经之路上。但其不参与到 TCP 连接中,它不会改变数据包的任何一个字段,只是在串联的链路防护,安全的数据包就会放过 WAF 到达目的地。
流量镜像

流量镜像(Traffic Mirroring)模式如上图所示,客户端与服务器间会经过交换机,这时可以使用交换机的端口镜像功能,将 Web 请求流量的原始帧镜像给 WAF,WAF 将数据帧还原成原始请求就可以对流量进行分析。