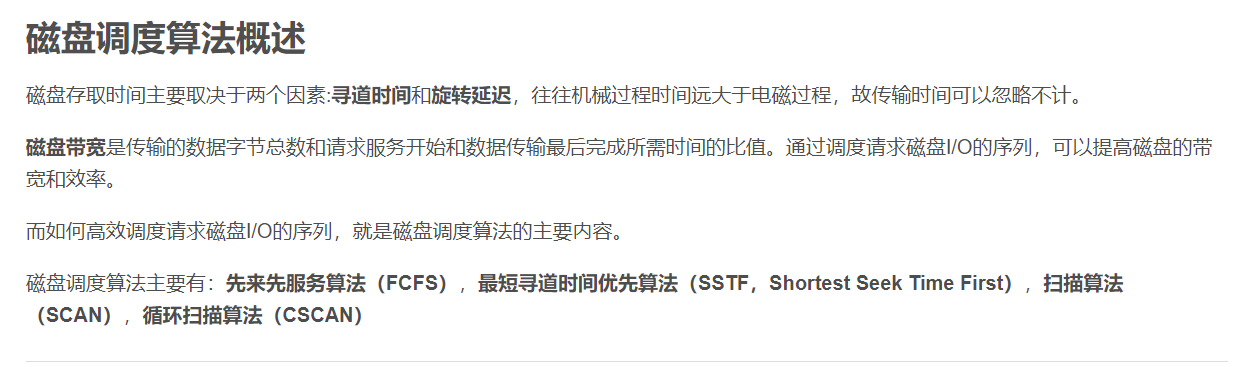
一 普通数组基础

首先，我们根据下图先了解一下什么是前缀和。

既然我们明白了前缀和是怎么回事，那我们就来看一下我们该怎么输入
先给出答案，然后再给出分析。
答案：

for (int i = 1; i <= n; i ++ ){cin >> a[i];s[i] = s[i - 1] + a[i];
}
1
2
3
4

我们通过这副图来理解一下为什么这么写代码就可以得到前缀和

到现在，我们已经解决了输入问题和前缀和的问题，下面就是我们如何利用前缀和的时候了。
我们用前缀和有一个很大的优势，就是可以快速的得到某一个区间的区间总和

前缀和的优势：以(o1)的时间复杂度得到某块区间的总和
好，我们先来看一下怎么求一个区间的和
我们用 L 和 R 分别表示区间的左右端点，
那么

好，前缀的内容就这么多啦
下面奉上我的代码

#include <iostream>using namespace std;const int N = 100010;int n, m;
int a[N], s[N];int main(){cin >> n >> m;for (int i = 1; i <= n; i ++ ) cin >> a[i], s[i] = s[i - 1] + a[i];while (m -- ){int l, r;cin >> l >> r;cout << s[r] - s[l - 1] << endl;}return 0;}

何为前缀和算法？
前缀和算法，属于基础算法，一般来说没有固定的模板，但是其思路值得借鉴，我们来看一个案例就懂了
作用： 快速求一段和，一般暴力算法时间复杂度为O（n）,而现在使用前缀和的时间复杂度可降为O（1）

具体实现：
求s[ l, r ]的区间和

for(int i = 1; i <= n; i++){s[i] = s[i-1] + a[i];
}
printf("%d",s[r] - s[l-1]);
1
2
3
4

值得注意的一点是，我们一般将S[0] = 0,原因如下：
假设我们需要计算S【1，10】，那么S10 - S0可以直接得出，Sr - S（l-1）

二 53. 最大子数组和

1 题目

2 解题思路

这道题要求的是最大子数组和。

对于子数组通常有两种处理方法：

前缀和；
滑动窗口
由于这道题是求和的，我们可以考虑使用前缀和来处理。

通过前缀和可以确定任意一个子数组的数组和。

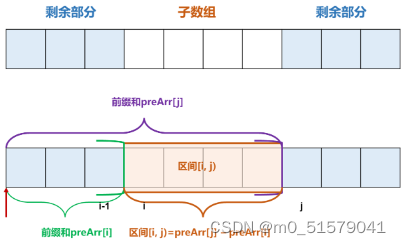
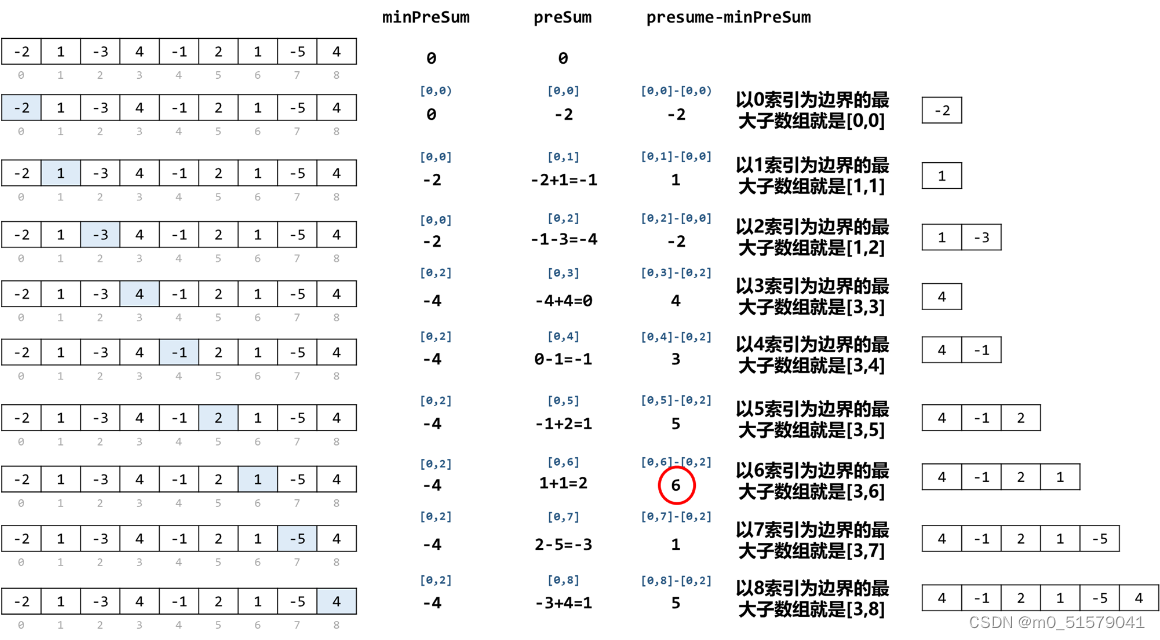
可以看到，子数组[i,j)的和是通过两个前缀和相减得到的。那么如果我们固定被减数 preArr[j]，那么只要减数最小，那么得到的子数组和就最大。

那么减数是什么？减数是 preArr[j] 之前出现过的前缀和。而最终得到的子数组是什么？是以 j 为右边界的和最大的子数组。

因此我们使用两个变量：

preSum： 累加当前位置的前缀和；
minPreSum： 记录当前位置之前的饿最小前缀和，初始为 0，表示子数组就是整个前缀。

图解算法过程

3 code

class Solution {
public:int maxSubArray(vector<int>& nums) {//最大子数组和，初始为极小值int res=INT_MIN;//当前元素之前的最小前缀和int minPreSum=0;//当前前缀和[0,1]int preSum=0;for(int num:nums){//累加前缀和preSum+=num;//当前前缀和-最小前缀和表示以当前元素为右边界的最大子数组和res=max(res,preSum-minPreSum);//更新最小前缀和minPreSum=min(minPreSum,preSum);}return res;}
};

三 56. 合并区间

1 题目

2 解题思路

首先我们明确合并两个区间的过程是什么：

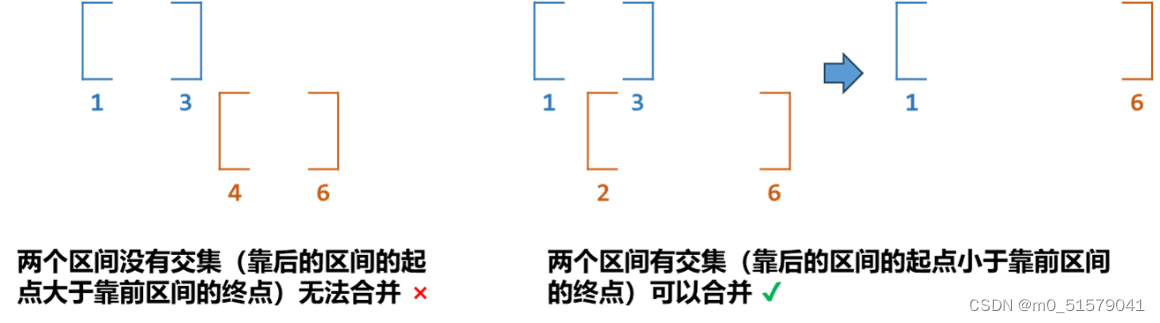
首先我们根据区间的起点做了一个排序，起点小的靠前，起点大的靠后；
其次我们根据前一个区间的终点和后一个区间的起点是否有重合，判断区间是否可以合并；
最后，合并后的区间起点一定是靠前的那个区间的起点，终点是两个区间中终点更大的那个；
从两个区间的合并过程中我们可以看出，合并区间：

根据区间起点排序；
维护一个当前合并的区间[start, end]
判断当前区间是否可以合并到当前的合并区间；可以则更新合并区间的终点，不可以这个区间作为新的一个合并区间去合并后面的区间。

3 code

class Solution {
public:vector<vector<int>> merge(vector<vector<int>>& intervals) {//对区间进行升序排序sort(intervals.begin(),intervals.end());//结果列表vector<vector<int>> res;//初始化合并区间的起点为首个区间的起点int start=intervals[0][0];//初始化合并区间的终点为首个区间的终点int end=intervals[0][1];int n=intervals.size();for(int i=0;i<n;i++){//判断每一个区间能否加入当前合并区间，//由于首个区间已经是初始的合并区间，//因此从第二个区间开始判断if(intervals[i][0]>end){//当前区间不能加入当前的合并区间，//记录当前合并区间。//以当前区间作为新的合并区间vector<int> ans={start,end};res.emplace_back(ans);start=intervals[i][0];end=intervals[i][1];}else{//当前区间加入当前的合并区间。//更新合并区间的终点end=max(end,intervals[i][1]);}}//补充加入最后一个合并区间vector<int> ans={start,end};res.emplace_back(ans);return res;}
};

四 56. 合并区间

1 题目

2 解题思路

3 code