其实这个问题很好回答,只需要运行如下代码,如下的基因列表是顺序是完全相同,并且我们只是做了最基础的变换
library(clusterProfiler)
library(org.Hs.eg.db)data(geneList, package="DOSE")ego1 <- gseGO(geneList = geneList,OrgDb = org.Hs.eg.db,ont = "CC",minGSSize = 100,maxGSSize = 500,pvalueCutoff = 0.05,verbose = FALSE)
geneList2 <- geneList + 5ego2 <- gseGO(geneList = geneList2,OrgDb = org.Hs.eg.db,ont = "CC",minGSSize = 100,maxGSSize = 500,pvalueCutoff = 0.05,verbose = FALSE)
geneList3 <- geneList * 100ego3 <- gseGO(geneList = geneList3,OrgDb = org.Hs.eg.db,ont = "CC",minGSSize = 100,maxGSSize = 500,pvalueCutoff = 0.05,verbose = FALSE)library(ggplot2)
p1 <- dotplot(ego1)
p2 <- dotplot(ego2)
p3 <- dotplot(ego3)
p1 + p2 + p3
但是结果中,geneList和geneList3最为接近,geneList2几乎完全不一样。
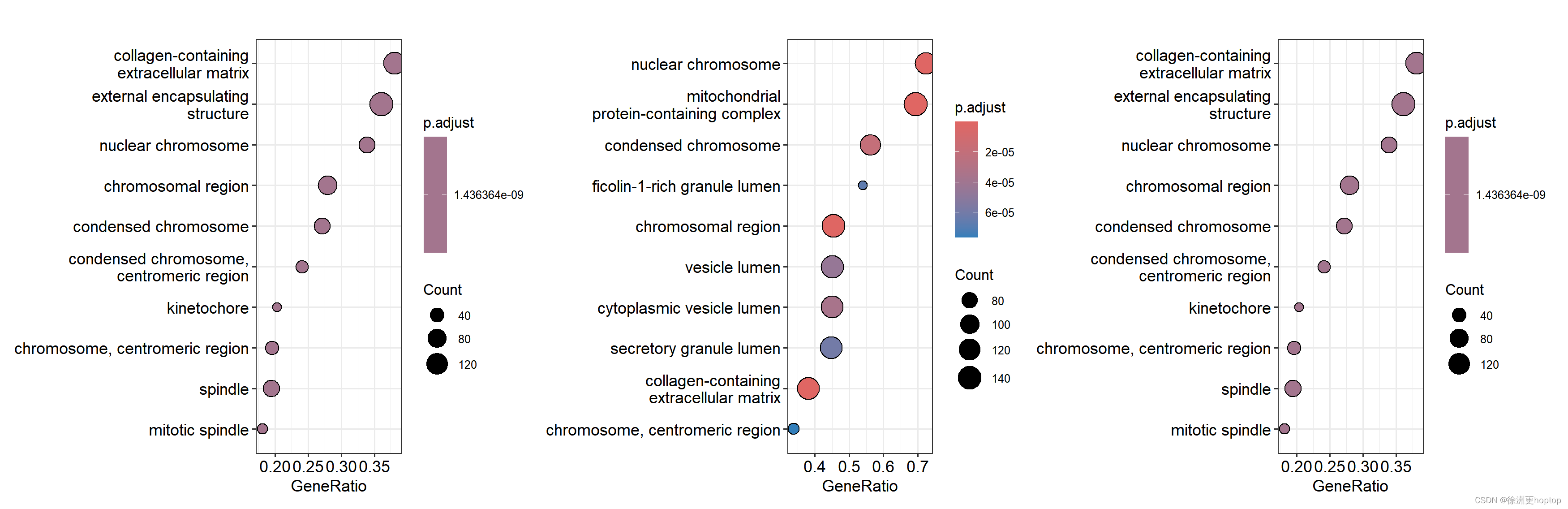
这说明GSEA肯定是不可能考虑排序的,因为它的算法过程中还有一个ES得分计算,这个计算用到的权重就来自于排序所用的得分。
Step 1: Calculation of an Enrichment Score. We calculate an enrichment score (ES) that reflects the degree to which a set S is overrepresented at the extremes (top or bottom) of the entire ranked list L. The score is calculated by walking down the list L, increasing a running-sum statistic when we encounter a gene in S and decreasing it when we encounter genes not in S. The magnitude of the increment depends on the correlation of the gene with the phenotype. The enrichment score is the maximum deviation from zero encountered in the random walk; it corresponds to a weighted Kolmogorov–Smirnov-like statistic (ref. 7 and Fig. 1B).
在GSEA发表的文章中提到了,这种增加和降低的比例就取决于基因和表型的相关性,也就是说,gene的得分很重要。目前的得分有如下流派
- pvalue / qvalue: 只考虑显著性
- log2FC: 考虑倍数变化
- -log10(pvalue) : 显著性的一种换算方式
- sign(log2FC) * -log10(pvalue): 有符号的显著性。
- 统计检验的值, AUC,… 类似于第一种方法。
问题来了,我们应该选择哪种呢?大家可以尝试检索下相关的文献研究哦





![[数据集][目标检测]旋风检测数据集VOC+YOLO格式157张1类别](https://img-blog.csdnimg.cn/direct/83778a7731d64af3bcf2e70a39acf8a0.png)