最小二乘法算法（个人总结版）

最小二乘法（Least Squares Method）是一种通过最小化误差平方和来拟合数据的回归分析方法。它被广泛应用于线性回归、多元回归以及其他数据拟合问题中。以下是详细的教程，涵盖基本概念、数学推导、具体步骤和实现代码。

1. 最小二乘法基本概念

最小二乘法是一种用于数据拟合的统计方法，通过最小化观测数据与模型预测值之间的误差平方和，求解模型参数。

2. 线性回归的最小二乘法

线性回归是最简单的最小二乘法应用，假设模型为线性关系： y=β0+β1x 其中，y 是响应变量，x 是自变量，β0 是截距，β1 是斜率。

3. 最小二乘法的数学推导

假设有 n 个观测数据点(xi,yi)，最小二乘法通过最小化以下误差平方和S 来求解模型参数：

为了找到最优参数 β0 和 β1，对 S 求偏导数并令其为零：

解这两个方程，得到：

4. 多元线性回归的最小二乘法

对于多元线性回归模型：

可以使用矩阵形式来表示和求解。设： y=Xβ+e 其中，y 是响应变量向量，X 是设计矩阵，β 是参数向量，e 是误差向量。

通过最小化误差平方和可以得到参数估计：

5. 非线性最小二乘法

非线性最小二乘法用于拟合非线性模型。这种情况下，通常需要使用迭代优化算法如梯度下降法、牛顿法等进行参数估计。

6. 最小二乘法的应用实例

例1：简单线性回归

假设有以下数据点：

(1,2),(2,2.8),(3,3.6),(4,4.5),(5,5.1)(1,2),(2,2.8),(3,3.6),(4,4.5),(5,5.1)

可以用最小二乘法拟合直线：

计算得到的最优参数为β0和β1。

例2：多元线性回归

假设有以下数据点和两个自变量：

(1,2,2),(2,2.8,3),(3,3.6,4),(4,4.5,5),(5,5.1,6)(1,2,2),(2,2.8,3),(3,3.6,4),(4,4.5,5),(5,5.1,6)

可以用最小二乘法拟合多元回归模型：

7. 最小二乘法的实现

Python实现示例：

import numpy as np
import matplotlib.pyplot as plt# 生成数据
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 2.8, 3.6, 4.5, 5.1])# 计算最小二乘法系数
A = np.vstack([x, np.ones(len(x))]).T
m, c = np.linalg.lstsq(A, y, rcond=None)[0]# 绘图
plt.plot(x, y, 'o', label='Original data', markersize=10)
plt.plot(x, m*x + c, 'r', label='Fitted line')
plt.legend()
plt.show()

步骤解析：

生成数据：创建自变量 x 和因变量 y 的数据点。
构建设计矩阵：将 x 和常数项 1 叠加构成设计矩阵 A。
求解最优参数：使用 numpy 的 lstsq 函数求解线性方程 Aβ=y 的最优参数 m 和 c。
绘制图表：绘制原始数据点和拟合直线。

最小二乘法图解

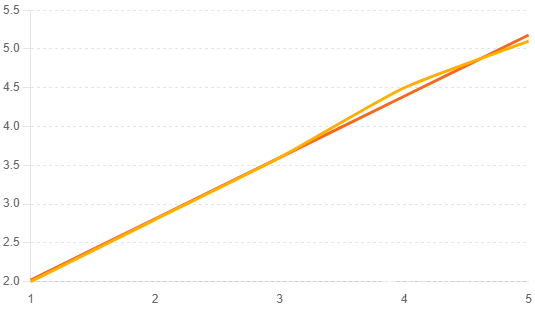
这是一个简单的最小二乘法线性回归的图表，用于演示如何通过最小二乘法拟合数据点。以下是图表的详细说明：

图表说明

X轴：自变量 x
Y轴：因变量 y
黄色圆点：原始数据点
红色直线：拟合直线，通过最小二乘法计算得到

图表生成代码

如果你想在自己的环境中生成类似的图表，可以使用以下Python代码：

import numpy as np
import matplotlib.pyplot as plt# 生成数据
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 2.8, 3.6, 4.5, 5.1])# 计算最小二乘法系数
A = np.vstack([x, np.ones(len(x))]).T
m, c = np.linalg.lstsq(A, y, rcond=None)[0]# 绘制图表
plt.figure(figsize=(10, 6))
plt.plot(x, y, 'o', label='Original data', markersize=10, color='orange')
plt.plot(x, m*x + c, 'r', label='Fitted line')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Least Squares Fit')
plt.legend()
plt.grid(True)
plt.show()