目录

1.什么是霍夫曼树

2.霍夫曼树的构造过程

3.霍夫曼编码

3.1具体的作用-频率统计

##实战题目

---

1.什么是霍夫曼树

给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

相关知识：
1、路径和路径长度
在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。
通路中分支的数目称为路径长度。若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
2、结点的权及带权路径长度
若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。
结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
3、树的带权路径长度
树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL。

2.霍夫曼树的构造过程

哈夫曼树的节点个数：
哈夫曼树是一种满二叉树，这意味着除了叶节点外，每个节点都有两个子节点。对于 (N) 个唯哈夫曼树的节点个数与输入的唯一字符数量有关。设字符集合的大小为 (N)（即有 (N) 个唯一字符），则哈夫曼树的节点数最小值和最大值如下：一字符，会有 (N) 个叶节点，每个叶节点代表一个字符。最小值
最小节点数：当输入的字符集合大小为 (N) 时，最小的哈夫曼树（也是理论上的最小值）会有 (2N - 1) 个节点。这是因为在构建哈夫曼树时，每次合并两个节点会创建一个新的内部节点，而最终只剩下一个节点（根节点）没有被合并。这意味着有(N-1) 次合并操作，每次合并操作增加一个新的内部节点，因此有 (N-1) 个内部节点和 (N) 个叶节点，总共 (2N - 1) 个节点。最大值
对于哈夫曼树，最大节点数的概念实际上并不适用，因为哈夫曼树的构建是基于字符的频率的，其目的是为了创建一个尽可能高效的编码方案。每个唯一字符都会成为树的一个叶节点，而内部节点的数量总是 (N-1)，所以节点总数固定为 (2N - 1)。不会有比这更多的节点数，因为这是根据哈夫曼算法的定义和工作方式所固有的。结论
对于 (N) 个唯一字符，哈夫曼树的节点数总是 (2N - 1)，这里没有最大值概念，因为节点总数是固定的，只要给定了唯一字符的数量。

哈夫曼树的构造过程：

假设有n个权值，则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn，则哈夫曼树的构造规则为：

(1) 将w1、w2、…，wn看成是有n 棵树的森林(每棵树仅有一个结点)；

(2) 在森林中选出两个根结点的权值最小的树合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；

(3)从森林中删除选取的两棵树，并将新树加入森林；

(4)重复(2)、(3)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。

3.霍夫曼编码

哈夫曼编码是一种压缩编码的编码算法，是基于哈夫曼树的一种编码方式。哈夫曼树又称为带权路径长度最短的二叉树。

哈夫曼编码跟 ASCII 编码有什么区别？

ASCII 编码是对照ASCII 表进行的编码，每一个字符符号都有对应的编码，其编码长度是固定的。而哈夫曼编码对于不同字符的出现频率其使用的编码是不一样的。其会对频率较高的字符使用较短的编码，频率低的字符使用较高的编码。这样保证总体使用的编码长度会更少，从而实现到了数据压缩的目的。

3.1具体的作用-频率统计

哈夫曼树是一个带权的二叉树，而在哈夫曼编码中，字符的出现频率就是字符的权重。因此要根据字符的频率放入优先队列中进行排序。然后根据这些字符构建一棵哈夫曼树

##代码实现

//c++代码实现
#include <iostream>
#include <vector>
using namespace std;
#include <algorithm> // 包含<algorithm>以使用reverse函数
#define MAXCODELEN 100
#define MAXHAFF 256 // 为了简化，假设最多处理256个不同的字符
#define MAXWEIGHT 10000typedef struct Haffman {//权重 int weight;//字符 char ch;//父节点，左儿子，右儿子 int parent, leftChild, rightChild;
} HaffmanNode;typedef struct Code {int code[MAXCODELEN];int start;
} HaffmanCode;HaffmanNode haffman[MAXHAFF * 2 - 1]; // 扩展数组大小以容纳所有可能的内部节点
HaffmanCode code[MAXHAFF];//构造哈夫曼树的过程 
void buildHaffman(int all) {//对每个节点进行初始化 //哈夫曼节点的个数总为 2 * all - 1 for (int i = 0; i < 2 * all - 1; i++) {haffman[i].weight = 0;haffman[i].parent = -1;haffman[i].leftChild = -1;haffman[i].rightChild = -1;}cout << "请输入需要哈夫曼编码的字符和权重大小" << endl;for (int i = 0; i < all; i++) {//获取每个字符及权重 cout << "请分别输入第" << i + 1 << "个哈夫曼字符和权重:" << endl;cin >> haffman[i].ch >> haffman[i].weight;}//用来存储两个最小权值的节点以及权重 int x1, x2, w1, w2;//all个节点，只需要合并all - 1 次，循环all - 1 次即可 for (int i = 0; i < all - 1; i++) {//初始化成不可能的值 x1 = x2 = -1;w1 = w2 = MAXWEIGHT;//遍历每一个可能的节点，包括初始的叶节点和已经创建的内部节点。 for (int j = 0; j < all + i; j++) {if (haffman[j].parent == -1) {//如果当前节点没有父节点 ，即还没有加入到haffman树中，即考虑这个节点 if (haffman[j].weight < w1) {w2 = w1;x2 = x1;//利用x1，和w1来接受第一个节点和权值 w1 = haffman[j].weight;x1 = j;}//利用x2，和w2来接受第二个节点和权值 else if (haffman[j].weight < w2) {w2 = haffman[j].weight;x2 = j;}}}//循环遍历一遍后，x1，x2，w1，w2即是最小两个节点的选择和权值 //将其加入到huffman树中 haffman[all + i].leftChild = x1;haffman[all + i].rightChild = x2;haffman[all + i].weight = w1 + w2;haffman[x1].parent = all + i;haffman[x2].parent = all + i;}
}void printCode(int all) {//遍历每一个字符-我们所输入的 for (int i = 0; i < all; i++) {//用来存储每一个字符的haffman编码 vector<int> hCode;int current = i;int parent = haffman[current].parent;//通过回溯到根节点，然后确保haffman编码的完整性 while (parent != -1) {//左孩子 '0' if (haffman[parent].leftChild == current) {hCode.push_back(0);}//右孩子 '1' else {hCode.push_back(1);}current = parent;parent = haffman[current].parent;}reverse(hCode.begin(), hCode.end());cout << haffman[i].ch << ": Huffman Code is: ";for (int j = 0 ; j < hCode.size() ; j++){cout << hCode[j] ;}	
//        for (int bit : hCode) {
//            cout << bit;
//        }cout << endl;}
}int main() {cout << "请输入有多少个哈夫曼字符:" << endl;int all = 0;cin >> all;if (all <= 0) {cout << "你输入的个数有误" << endl;return -1;}buildHaffman(all);printCode(all);return 0;
}

#python代码
import heapq
from collections import defaultdict, Counter# 定义树的节点
class Node:def __init__(self, char, freq):self.char = charself.freq = freqself.left = Noneself.right = None# 为了让节点能在优先队列中按频率排序，定义比较方法def __lt__(self, other):return self.freq < other.freq# 构建哈夫曼树
def build_huffman_tree(text):# 统计字符频率frequency = Counter(text)# 创建优先队列priority_queue = [Node(char, freq) for char, freq in frequency.items()]heapq.heapify(priority_queue)# 循环直到队列中只剩一个元素while len(priority_queue) > 1:# 弹出两个最小元素left = heapq.heappop(priority_queue)right = heapq.heappop(priority_queue)# 创建新的内部节点，将两个节点作为子节点merged = Node(None, left.freq + right.freq)merged.left = leftmerged.right = right# 将新节点加入优先队列heapq.heappush(priority_queue, merged)# 队列中剩下的元素就是树的根节点return priority_queue[0]# 生成哈夫曼编码
def generate_codes(node, prefix="", code={}):if node is not None:if node.char is not None:code[node.char] = prefixgenerate_codes(node.left, prefix + "0", code)generate_codes(node.right, prefix + "1", code)return code# 编码文本
def encode(text, codes):return ''.join(codes[char] for char in text)# 解码文本
def decode(encoded_text, root):decoded_text = ""current_node = rootfor bit in encoded_text:if bit == '0':current_node = current_node.leftelse:current_node = current_node.rightif current_node.char is not None:decoded_text += current_node.charcurrent_node = rootreturn decoded_text# 主函数
# def main():
#     text = "this is an example for huffman encoding"
#     root = build_huffman_tree(text)
#     codes = generate_codes(root)
#     encoded_text = encode(text, codes)
#     decoded_text = decode(encoded_text, root)
#
#     print(f"Original text: {text}")
#     print(f"Encoded text: {encoded_text}")
#     print(f"Decoded text: {decoded_text}")# if __name__ == "__main__":
#     main()# 主函数
def main():text = "this is an example for huffman encoding"root = build_huffman_tree(text)codes = generate_codes(root)# 打印每个字符的哈夫曼编码print("Huffman Codes for each character:")for char, code in codes.items():print(f"'{char}': {code}")encoded_text = encode(text, codes)decoded_text = decode(encoded_text, root)print(f"\nOriginal text: {text}")print(f"Encoded text: {encoded_text}")print(f"Decoded text: {decoded_text}")if __name__ == "__main__":main()

##实战题目

3531. 哈夫曼树 - AcWing题库

##示例代码

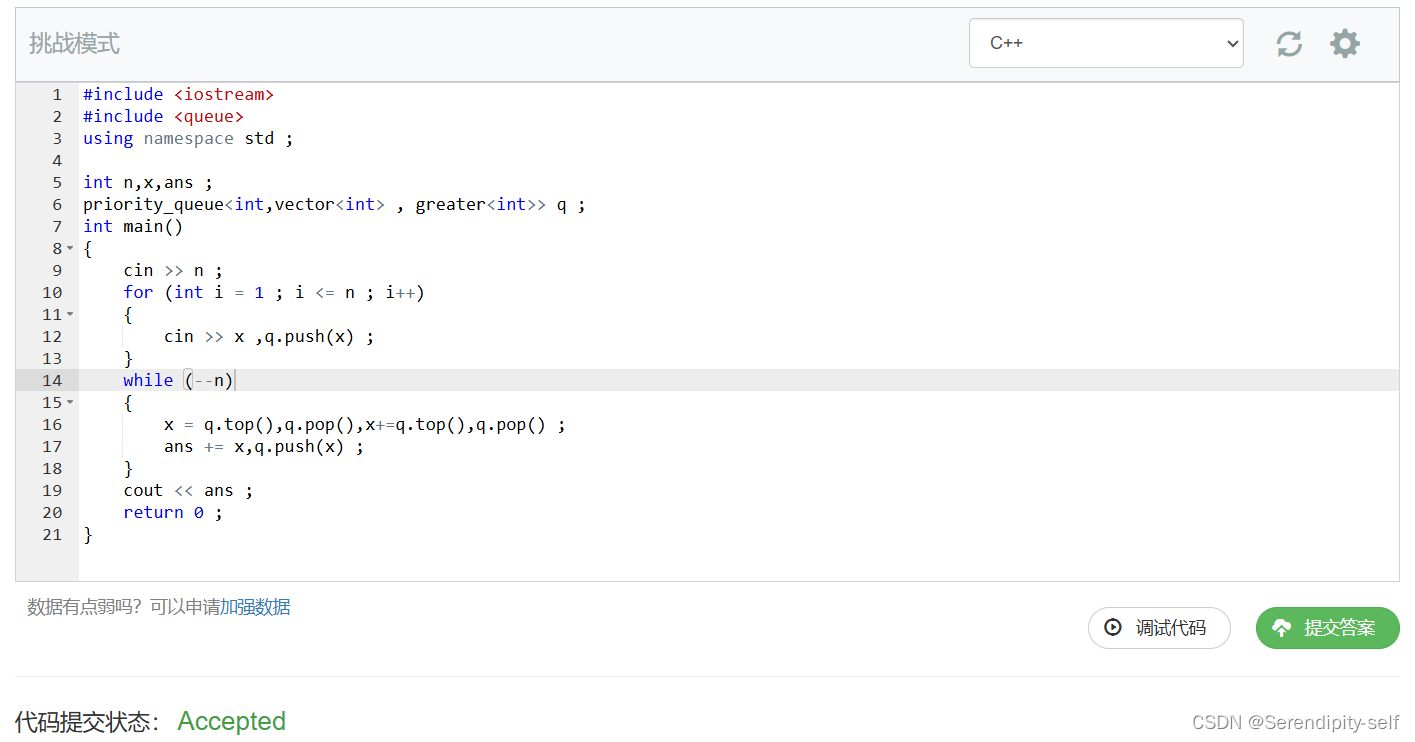
//c++代码
#include <iostream>
#include <queue>
using namespace std;int n, x, ans;
priority_queue <int, vector <int>, greater <int> > q;int main ()
{cin >> n;for (int i = 1; i <= n; i ++){cin >> x, q.push (x); // 加入二叉堆（优先队列）}while (-- n){x = q.top (), q.pop (), x += q.top (), q.pop (); // 取出两个堆顶（当前最小值）合并ans += x, q.push (x); // 统计答案，在放进堆中}cout << ans;return 0;
}

 148. 合并果子 - AcWing题库

 149. 荷马史诗 - AcWing题库

##代码示例

//c++代码示例
#include<bits/stdc++.h>
using namespace std ;typedef long long LL ;
typedef pair<LL,int> PLI ;
const int N = 1e5 + 10 ;int n , m ;
priority_queue<PLI,vector<PLI>,greater<PLI>> p ;int main()
{cin >> n >> m ;for (int i = 1 ; i <= n ; i++){LL w ;cin >> w ;p.push({w,0}) ;}//这是因为在每次合并操作中，会从堆中取出 m 个节点并合并为一个新节点，这意味着总节点数将减少 m−1。//为了最终能够合并到只剩一个节点，初始的节点数 n 与合并的分支数 m 必须满足 n - 1 是 m - 1 的倍数。while ((n - 1) % (m - 1)){p.push({0ll,0}) ;n++ ;}LL ans = 0 ; while (p.size() > 1){LL sum = 0 ;int depth = 0 ;for (int i = 1 ; i <= m ; i++){sum += p.top().first ;depth = max(depth, p.top().second) ;p.pop() ;}ans += sum ;p.push({sum,depth+1}) ;}cout << ans << endl << p.top().second ;return 0 ;
}