1 递归返回情况

        （1）结点包含样本全为同一类别

        （2）属性集为空，没有属性可供划分了

                或

                有属性，但是在属性上划分的结果都一样

        （3）结点为空结点

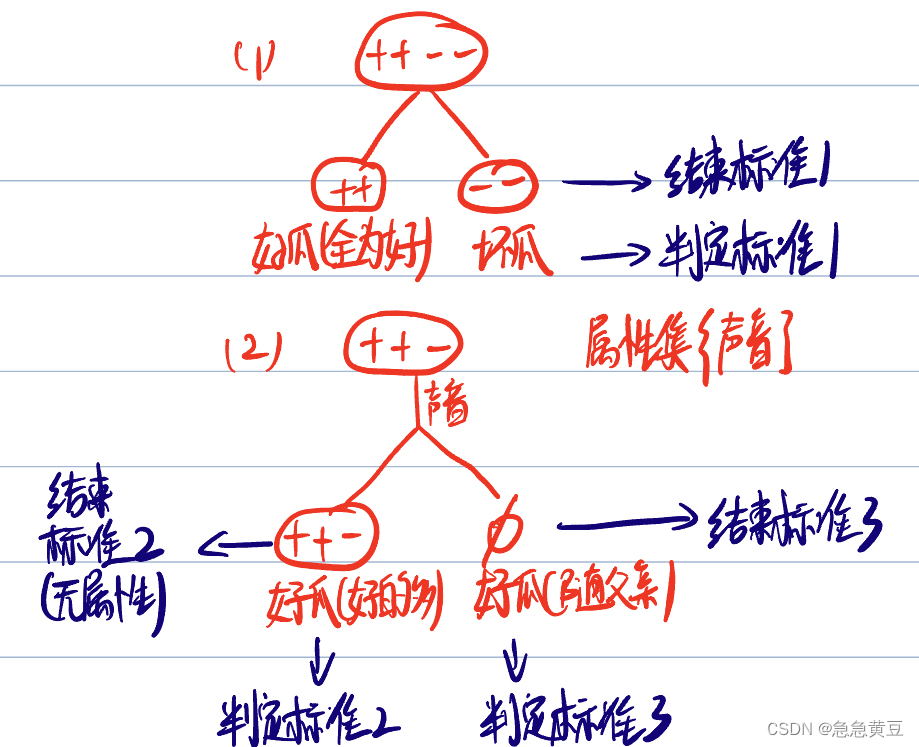
**结束时判定该结点的类别遵循如下规则：

        （1）若全为一个类别，则该结点为该类别，如全为“好瓜”，则该结点为好瓜

        （2）若某一个类别比其他类别多，则该结点为该类别，如结点中的样本“好瓜”>“坏瓜”，则该结点为好瓜。

        （3）若所有类别样本数一样，或为空集，则取其父节点的类别作为该结点的类别。

2.经典的属性划分方法

2.1.信息增益(选大)

• 求样本集的信息熵，信息熵越小，则集合越纯，如果集合只属于1个类别，那么信息熵为0
• 求每个属性每个取值的信息熵，这些信息熵按比例相加
• 求每个属性的信息增益，等于样本集信息熵减去该属性的加权信息熵
• 信息熵Ent(D)越小，数据集D的纯度越高
• 信息增益越大，则使用该属性来进行划分所获得的“纯度提升”越大
• 

2.2.增益率(选大)

• 信息增益对可取值数目较多的属性有所偏好，所以用增益率克服这一缺点
• 选择增益率大的属性，即选择信息增益大且分支少的属性
• 

2.3.基尼指数(选小)

• 反映了从D中随机抽取两个样本，其类别标记不一致的概率
• Gini(D)越小，数据集D的纯度越高
• 

3.剪枝处理

        划分选择的各种准则虽然对决策树的尺寸有较大影响，但对泛化性能的影响很有限；而剪枝方法和程度对决策树泛化性能的影响更为显著。（也就是说选择剪枝方法比选基尼指数、信息增益还是增益率这种划分策略的影响更大）

        是对付“过拟合”的主要手段，剪枝的基本策略：

3.1.预剪枝

1. 采用基于分层采样的留出法，初始认为所有样本都是好的，此时可计算模型的正确率为验证集中好瓜的比例。
2. 运用一种属性划分方法选择出一个最好的属性进行划分，划分之后计算加了一层之后的正确率，并与未引入划分的正确率进行比较，若划分后的正确率>未划分就生成，否则不生成。

---

3.2.后剪枝

        先生成完整的决策树，再倒着看每棵子树是否有价值。如果剪枝后的树>未剪枝的树则剪枝，否则不剪，当正确率相等时不做操作，一方面是防止欠拟合，一方面是剪枝也会有一定的开销。

4.连续值处理 

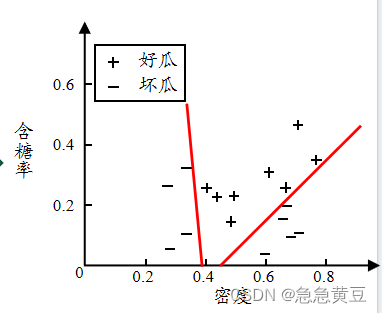
• 与离散属性不同，若当前结点划分属性为连续属性，该属性还可作为其后代结点的划分属性。也就是在某个点算出按密度<0.35和密度>0.35划分，后面在计算时还要把密度纳入考虑范围，且下次的划分点可能就不是0.35了。而别的离散属性比如颜色，如果用过就从属性集合中删去了。
• 方法：二分法
• 

5.缺失值处理

• 样本赋权，权重划分 

单变量决策树

 

多变量决策树