数据结构 —— 堆

1.堆的概念及结构

堆是一种特殊的树形数据结构，称为“二叉堆”（binary heap）

看它的名字也可以看出堆与二叉树有关系：其实堆就是一种特殊的二叉树

堆的性质：

  • 堆中某个结点的值总是不大于或不小于其父结点的值；
  • 堆总是一棵完全二叉树

1.1大堆

大堆：

  • 大堆的根节点是整个堆中最大的数
  • 每个父节点的值都大于或等于其孩子节点的值
  • 每个父节点的孩子之间并无直接的大小关系

1.2小堆 

小堆：

  •  小堆的根节点是整个堆中最小的数
  • 每个父节点的值都小于或等于其孩子节点的值
  • 每个父节点的孩子之间并无直接的大小关系

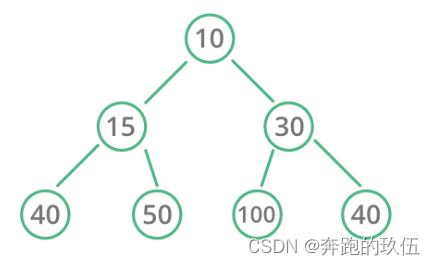
 2.堆的实现

2.1使用数组结构实现的堆

由于堆是一个完全二叉树，所以堆通常使用数组来进行存储

使用数组的优点：

  • 相较于双链表更加的节省内存空间
  • 相较于单链表可以更好的算父子关系，并找到想要找的父子

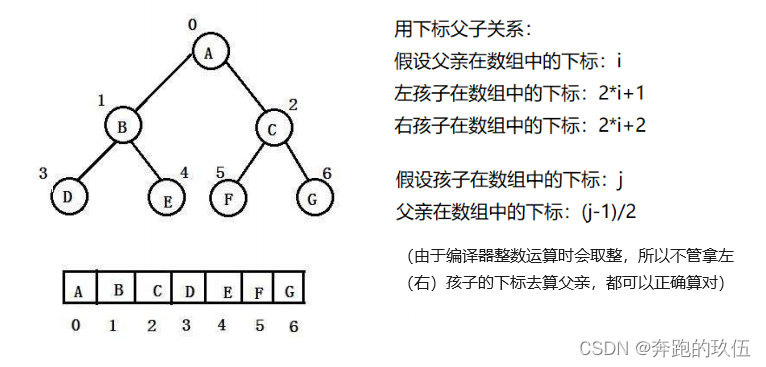
2.2堆向上调整算法

堆的向上调整（也称为堆化、堆的修复或堆的重新堆化）是堆数据结构维护其性质的关键操作之一

现在我们给出一个数组，逻辑上看做一颗完全二叉树。我们通过从最后一个叶子节点开始的向上调整算法可以把它调整成一个小堆
向下调整算法有一个前提：最后一个叶子之前是一个堆才能调整

 int arr = [ 15, 18, 19, 25, 28, 34, 65, 49, 37, 10]

小堆演示向上调整算法演示过程

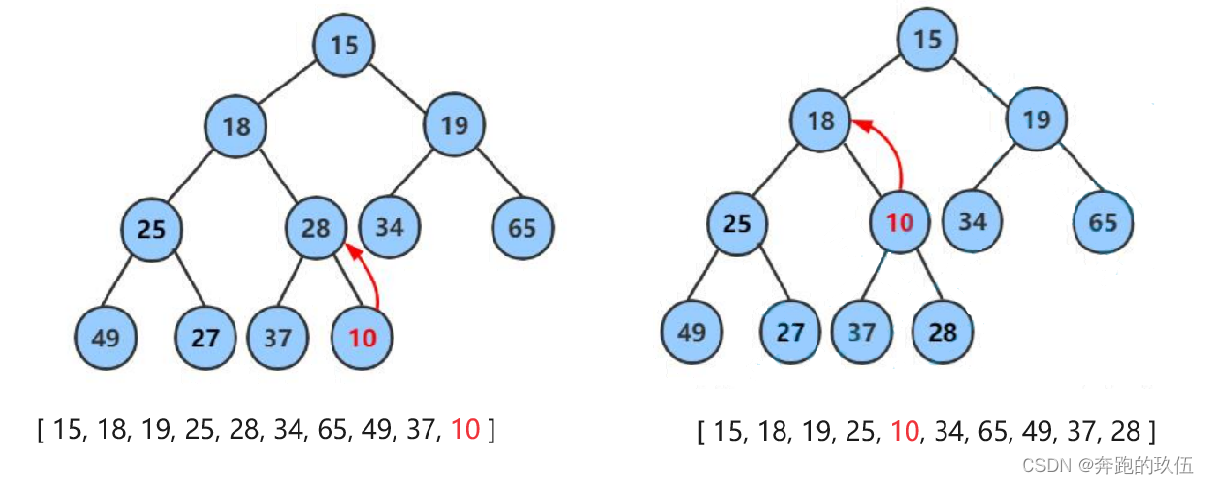
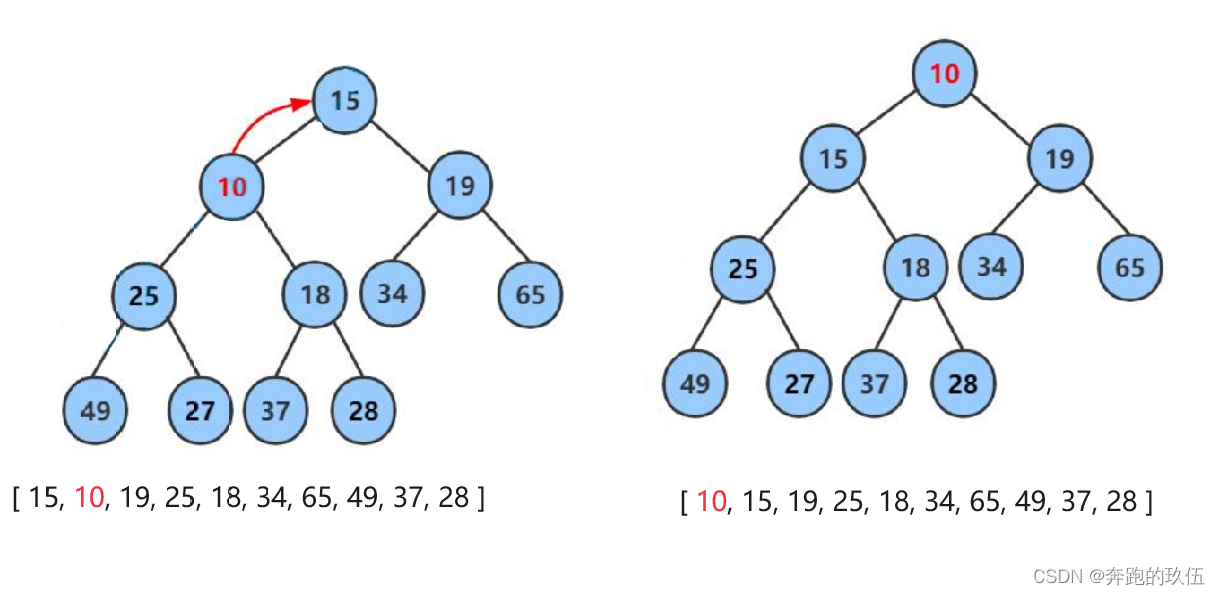
向上调整的过程 ：将新插入的值与它的父亲相比，如果小则向上调整，调整完成后与新的父亲去比较，直到其值 >= 父亲的时候停止调整 

void Swaps(HPDataType* a, HPDataType* b) {HPDataType temp;temp = *a;*a = *b;*b = temp;
}//向上调整(小堆)
//child是下标void AdjustUp(HPDataType* a, int child) {assert(a);int parent = (child - 1) / 2;//算父亲节点的下标//向下调整主要逻辑while (child > 0)     //当调整至根节点时，已经调整至极限，不用在调整{//当父亲节点 > 孩子时，开始调整if (a[parent] > a[child])     {Swaps(&a[child],&a[parent]);    //交换child = parent;                //走到新的位置为新一轮的向下调整做准备parent = (child - 1) / 2;     //算出新位置的父亲节点下标}//当父亲节点 < 孩子时,说明调整已经完毕，退出循环else{break;}}
}

2.3堆向下调整算法

在堆排序或其他需要维护堆性质的场景中，当堆的某个节点不满足堆的性质（对于最大堆，父节点小于其子节点；对于最小堆，父节点大于其子节点）时，就需要通过向下调整来修复这个子树，使其重新成为堆

现在我们给出一个数组，逻辑上看做一颗完全二叉树。我们通过从根结点开始的向下调整算法可以把它调整成一个小堆
向下调整算法有一个前提：左右子树必须是一个堆，才能调整
int array[] = {27,15,19,18,28,34,65,49,25,37};

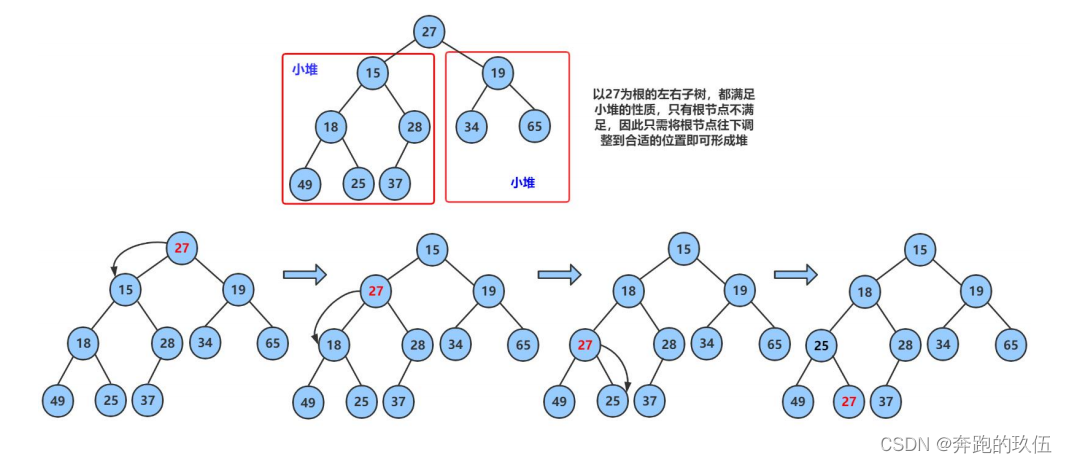
 2.4堆的插入

堆的插入（HeapPush)：通常通过将新元素添加到堆的末尾，并通过向上调整算法来维持堆的性质 (由于插入前的堆肯定是一个标准的堆，所以我们在将数据插入后执行一次向上调整算法，即可完成堆的插入)

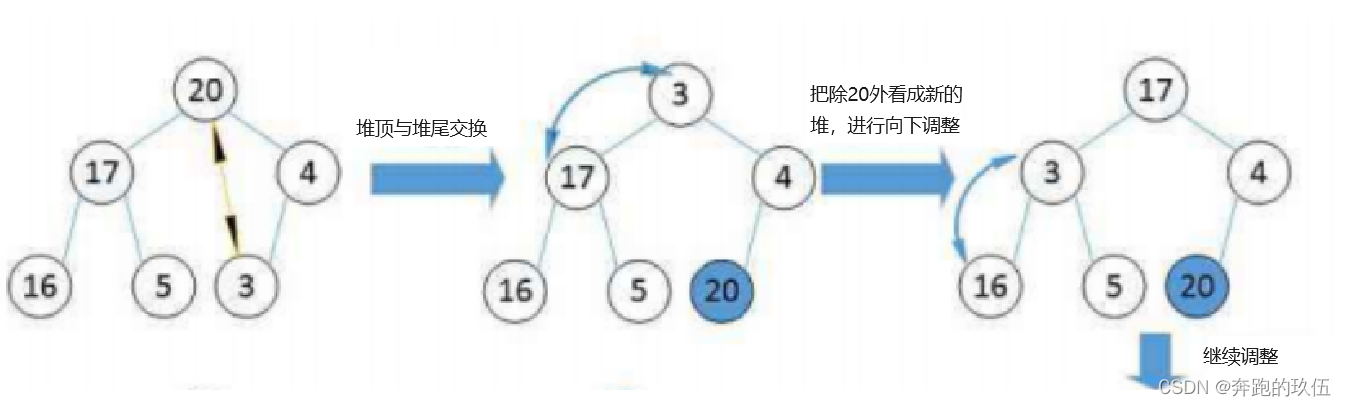
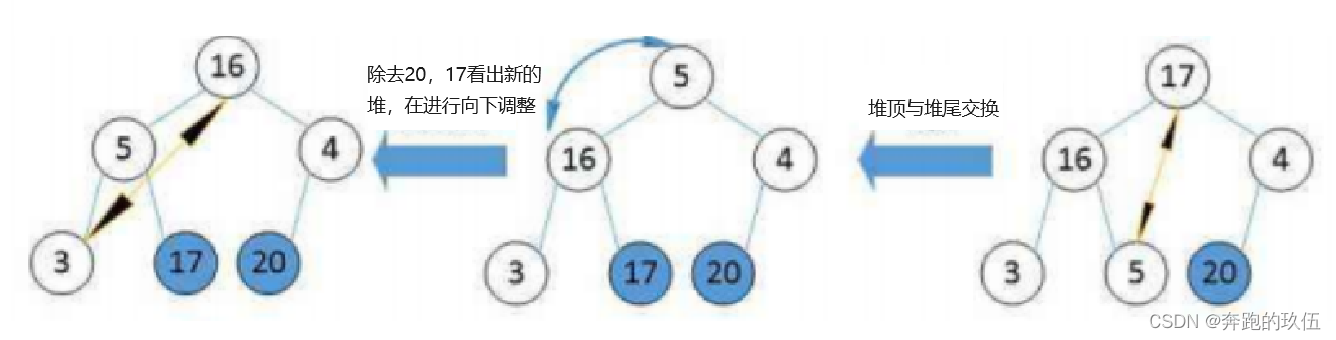
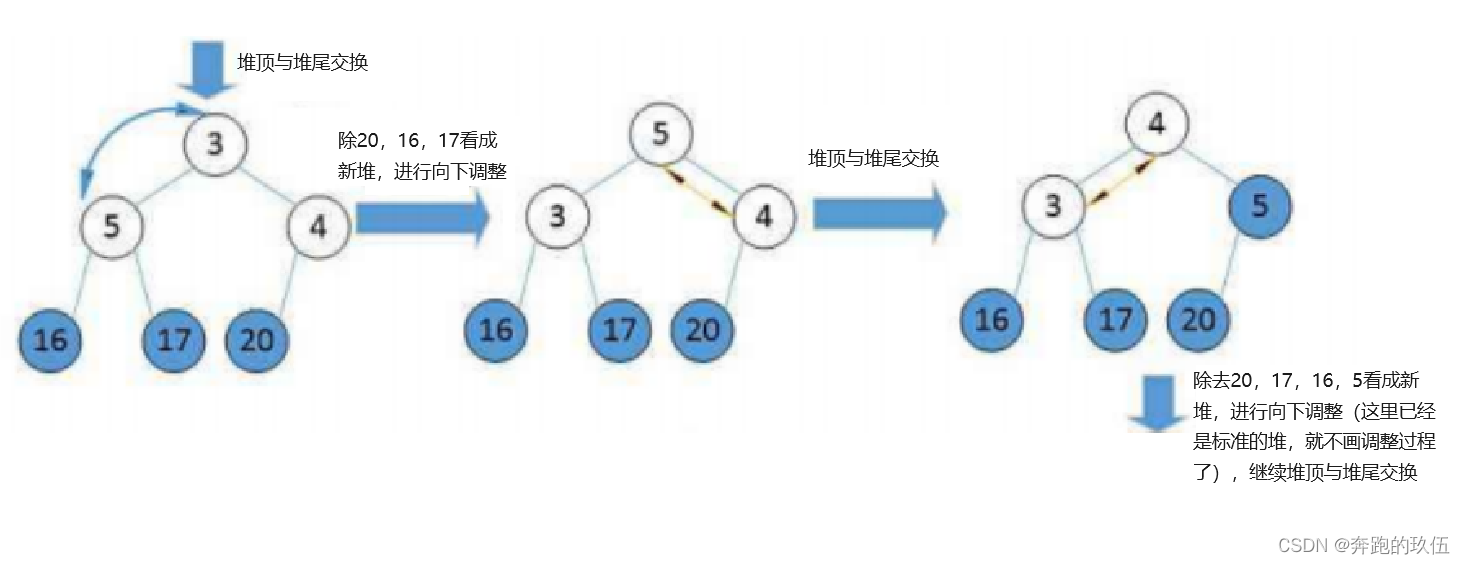
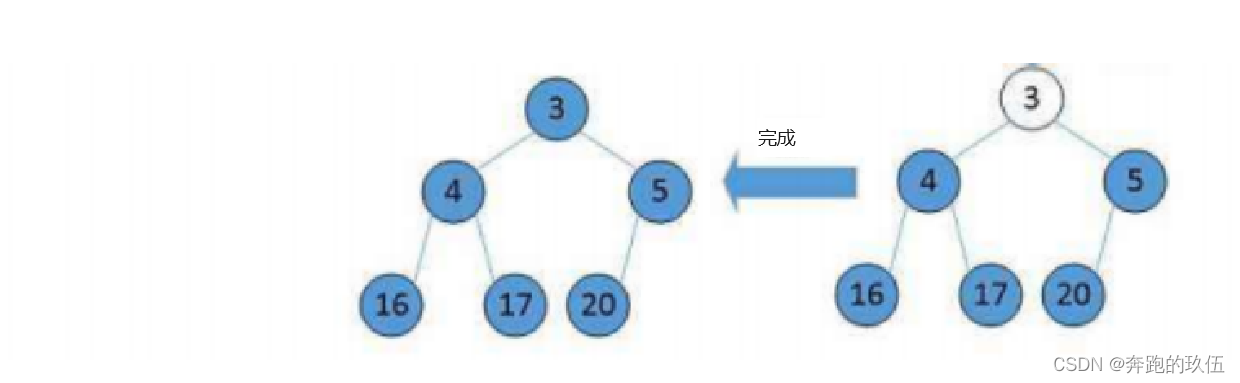
2.5堆的删除

删除元素（HeapPop）：在最大堆或最小堆中，通常删除的是根节点（即最大或最小元素），并通过向下调整算法来维持堆的性质 (由于删除前的堆肯定是一个标准的堆即左右子树肯定也是标准的堆，所以我们在将数据删除后执行一次向下调整算法，即可完成堆的删除)

为什么要删除根节点？

  • 相较于删除别的位置的节点，每次删除的根节点都是堆中最大或最小的数（大堆为最大，小堆为最小）、
  • 从根节点开始删除并调整堆结构，在实现上相对简便。只需删除后算法向下调整即可

2.6堆的代码实现

Heap.h

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>typedef int HPDataType;
typedef struct Heap
{HPDataType* _a;int _size;int _capacity;
}Heap;//堆的初始化
void HeapInit(Heap* php);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);//向上调整
void AdjustUp(HPDataType* a, int child);
//向下调整
void AdjustDown(HPDataType* a, int n, int parent);

Heap.c 

//堆的初始化
void HeapInit(Heap* hp) {assert(hp);hp->_a = NULL;hp->_capacity = hp->_size = 0;
}
// 堆的销毁
void HeapDestory(Heap* hp) {assert(hp);free(hp->_a);hp->_capacity = hp->_size = 0;}
// 堆的插入
void HeapPush(Heap* hp, HPDataType x) {assert(hp);//扩容if (hp->_size == hp->_capacity){int newcapacity = hp->_capacity == 0 ? 2 : hp->_capacity * 2;HPDataType* newa = (HPDataType*)realloc(hp->_a, newcapacity * sizeof(HPDataType));if (newa == NULL){perror("realloc");return;}hp->_capacity = newcapacity;hp->_a = newa;}//插入数据hp->_a[hp->_size] = x;hp->_size++;//向上调整AdjustUp(hp->_a,hp->_size-1);}
void Swaps(HPDataType* a, HPDataType* b) {HPDataType temp;temp = *a;*a = *b;*b = temp;
}
//向上调整(小堆)
//child是数组的下标
void AdjustUp(HPDataType* a, int child) {assert(a);int parent = (child - 1) / 2;while (child > 0){if (a[parent] > a[child]){Swaps(&a[child],&a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
// 堆的删除
void HeapPop(Heap* hp) {assert(hp);assert(hp->_size);//删除顶部数据  ，先与末尾的交换，在向下调整Swaps(&hp->_a[0],&hp->_a[hp->_size-1]);//让数组首元素，与尾元素交换位置hp->_size--;AdjustDown(hp->_a, hp->_size, 0);}
//向下调整(小堆)
//n是数据数个数
void AdjustDown(HPDataType* a, int n, int parent) {assert(a);//假设法，默认两个孩子最小的是左孩子int child = parent * 2 + 1;//当没有左孩子的时候停止向下调整,拿新算的孩子位置去判断while (child < n){if (child + 1 < n && a[child + 1] < a[child])//挑最小的孩子换，且要注意有没有右孩子{child += 1;}if (a[child] < a[parent])//孩子比父亲小就往上换{Swaps(&a[child], &a[parent]);parent = child;//孩子变成父亲，与他的孩子比child = parent * 2 + 1;}else{break;}}}
// 取堆顶的数据
HPDataType HeapTop(Heap* hp) {assert(hp);assert(hp->_size);return hp->_a[0];
}
// 堆的数据个数
int HeapSize(Heap* hp) {assert(hp);return hp->_size;
}
// 堆的判空
int HeapEmpty(Heap* hp) {return hp->_size == 0;
}

3堆的应用 — 堆排序 

堆排序，我们肯定是运用堆这个数据结构来完成我们的堆排序

接下来我们将充分的了解堆排序的运作原理

不难看出

  • 在每次交换时，堆顶最小的数都会沉到当前堆底
  • 小堆在经历过N（数据个数）轮后就会得到一个升序的数组
  • 大堆在经历过N（数据个数）轮后就会得到一个降序的数组

知道了堆排序的运转过程之后还有一个问题：使用者不可能说给你一个堆结构让你排序，肯定给的是一串无序且不是堆的数组给你排，这时侯我们就要考虑如何建堆了

3.1建堆

难道说建堆要用到上面写的堆结构，一个一个的去push吗？

其实不然，我们只需要使用向上调整算法或向下调整算法就可以完成建堆

向上调整建堆法

1.构建过程：

  • 初始时，将数组的第一个元素视为堆的根节点（对于下标从0开始的数组，根节点的下标为0）
  • 对于数组中剩余的元素（从下标1开始），将它们逐个视为“新插入”的元素，并执行向上调整操作
  • 在向上调整过程中，对于当前元素，首先计算其父节点的下标（parent = (child - 1) / 2）。然后，比较当前元素与其父节点的值
  • 如果当前元素的值大于其父节点的值（对于大根堆），则交换它们的位置。然后，将当前元素设置为新交换位置的父节点，并重复上述步骤，直到当前元素的值不大于其父节点的值或已经到达根节点
  • 通过重复上述步骤，直到所有元素都被处理过，最终得到的数组将满足堆的性质

2.时间复杂度：

  • 向上调整建堆法的时间复杂度为O(N * logN)，其中N是数组中的元素数量
void Swaps(int* a, int* b) {int temp;temp = *a;*a = *b;*b = temp;
}//向上调整(小堆)
void AdjustUp(int* a, int child) {assert(a);int parent = (child - 1) / 2;while (child > 0){if (a[parent] > a[child]){Swaps(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}//堆排序
void HeapSort(int* a, int n) {//创建堆，向上调整建堆for (int i = 1; i < n; i++) {AdjustUp(a,i);}}

向下调整建堆法

向下调整（Adjust Down）是指从给定的非叶子节点开始，通过与其子节点比较并交换位（如果需要）来确保堆的性质

1.构建过程

  1. 确定开始位置：
    • 对于长度为n的数组，由于堆是完全二叉树，所以最后一个非叶子节点的下标为(n-1-1)/2（整数除法）
    • 从这个下标开始，向前遍历所有非叶子节点
  2. 执行向下调整
  3. 遍历结束：
    • 当所有非叶子节点都经过向下调整后，整个数组就形成了一个堆

2.时间复杂度

向下调整建堆法的时间复杂度为O(N)，其中N是数组中的元素数量

void Swaps(int* a, int* b) {int temp;temp = *a;*a = *b;*b = temp;
}
//向上调整(小堆)
void AdjustUp(int* a, int child) {assert(a);int parent = (child - 1) / 2;while (child > 0){if (a[parent] > a[child]){Swaps(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}//堆排序
void HeapSort(int* a, int n) {//创建堆，向下调整建堆int parent = (n - 1 - 1) / 2;    //找到最后一个非叶子节点for (parent; parent >= 0; parent--){AdjustDown(a, n, parent);}}

3.2 利用堆删除思想来进行排序

void Swaps(int* a, int* b) {int temp;temp = *a;*a = *b;*b = temp;
}//向上调整(小堆)
void AdjustUp(int* a, int child) {assert(a);int parent = (child - 1) / 2;while (child > 0){if (a[parent] > a[child]){Swaps(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}//向下调整(小堆)
void AdjustDown(int* a, int n, int parent) {assert(a);int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] < a[child]){child += 1;}if (a[child] < a[parent]){Swaps(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}//堆排序
void HeapSort(int* a, int n) {创建堆，向上调整建堆//for (int i = 1; i < n; i++)//{//	AdjustUp(a, i);//}//创建堆，向下调整建堆int parent = (n - 1 - 1) / 2;for (parent; parent >= 0; parent--){AdjustDown(a, n, parent);}//小堆，可以排降序while (n){Swaps(&a[0], &a[n - 1]);//交换完成把除了最后一个数据之外的数组看成一个新的堆,开始向下交换，形成新的小堆n--;AdjustDown(a, n, 0);}}

4堆的应用 — Top-K问题

TOP-K 问题：即求数据结合中前 K 个最大的元素或者最小的元素，一般情况下数据量都比较大
比如：专业前 10 名、世界 500 强、富豪榜、游戏中前 100 的活跃玩家等
对于 Top-K 问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了 ( 可能 数据都不能一下子全部加载到内存中) 。最佳的方式就是用堆来解决，基本思路如下：
1. 用数据集合中前 K 个元素来建堆
  • 前k个最大的元素，则建小堆
  • 前k个最小的元素，则建大堆
2. 用剩余的 N-K 个元素依次与堆顶元素来比较，不满足则替换堆顶元素
将剩余 N-K 个元素依次与堆顶元素比完之后，堆中剩余的 K 个元素就是所求的前 K 个最小或者最大的元素。 

void Swaps(int* a, int* b) {int temp;temp = *a;*a = *b;*b = temp;
}//向下调整(小堆)大的下去
//n是数据数个数
void AdjustDown(HPDataType* a, int n, int parent) {assert(a);int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] < a[child]){child += 1;}if (a[child] < a[parent]){Swaps(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}
void CreateNDate()
{// 造数据int n = 10000;srand((unsigned int)time(NULL));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error");return;}for (size_t i = 0; i < n; ++i){int x = rand() % 1000000;fprintf(fin, "%d\n", x);}fclose(fin);
}void PrintTopK(int k) {//找出前K个最大的数//打开文件FILE* p = fopen("data.txt", "r");if (p == NULL){perror("fopen error");return;}//构建一个小堆int x = 0;int arr[10] = { 0 };for (int i = k; i < 10; i++){fscanf(p,"%d", &x);arr[i] = x;}//创建堆，向下调整建堆,F(N)int parent = (k - 1 - 1) / 2;for (parent; parent >= 0; parent--){AdjustDown(arr, k, parent);//这里的n数组的位置，里面的child会算出超过数组的位置，这样会停下来}//在将后面的数字依次对比小堆顶部，比它大就向下调整while (fscanf(p, "%d", &x) > 0){if (arr[0] < x){arr[0] = x;AdjustDown(arr, k, 0);}}for (int i = 0; i < k; i++){printf("%d\n", arr[i]);}
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/347963.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Vuepress 2从0-1保姆级进阶教程——标准化流程(Tailwindcss+autoprefixer+commitizen)

Vuepress 2从0-1保姆级进阶教程——标准化流程(Tailwindcss+autoprefixer+commitizen)

Vuepress 2 专栏目录【已完结】 1. 入门阶段 Vuepress 2从0-1保姆级入门教程——环境配置篇Vuepress 2从0-1保姆级入门教程——安装流程篇Vuepress 2从0-1保姆级入门教程——文档配置篇Vuepress 2从0-1保姆级入门教程——主题与部署 2.进阶阶段 Vuepress 2从0-1保姆级进阶教程—…
阅读更多...
AM273X毫米波演示

AM273X毫米波演示

介绍 毫米波演示展示了 AM273X SOC 使用毫米波 SDK&#xff08;软件开发工具包&#xff09;中的驱动程序的一些功能。它允许用户指定chirp配置文件并实时显示检测到的对象和其他信息。 以下是此演示功能的高级描述&#xff1a; 能够通过 UART 端口上的命令行界面 &#xff08;…
阅读更多...
文字悬停效果

文字悬停效果

文字悬停效果 效果展示 CSS 知识点 CSS 变量使用回顾-webkit-text-stroke 属性的运用与回顾 页面整体结构实现 <ul><li style"--clr: #e6444f"><a href"#" class"text">First</a></li><li style"--cl…
阅读更多...
苹果WWDC重磅发布的IOS 18、Apple Intelligence背后的技术分析！

苹果WWDC重磅发布的IOS 18、Apple Intelligence背后的技术分析！

2024年6月10日&#xff0c;在2024年WWDC全球开发者大会上&#xff0c;苹果推出了Apple Intelligence&#xff0c;这是深度集成到iOS 18、iPadOS 18和macOS Sequoia中的个人智能系统。 为了让大模型能在 iPhone 端侧跑&#xff0c;苹果还是做了很多事情的。接下来就跟大家介绍一…
阅读更多...
Spring学习笔记

Spring学习笔记

1 spring介绍 1)为什么学习spring ​ 1. Spring技术是JavaEE开发必备技能&#xff0c;企业开发技术选型命中率>90% ​ 2. 简化开发&#xff0c;降低企业级开发的复杂性 ​ 3. 框架整合&#xff0c;高效整合其他技术&#xff0c;提高企业级应用开发与运行效率 ​ 作为一…
阅读更多...
IDEA创建Mybatis项目

IDEA创建Mybatis项目

IDEA创建Mybatis项目 第一步&#xff1a;创建库表 -- 创建数据库 create database mybatis_db;-- 使用数据库 use mybatis_db;-- 创建user表 CREATE TABLE user (id INT AUTO_INCREMENT PRIMARY KEY,username VARCHAR(50) NOT NULL,password VARCHAR(50) NOT NULL,email VARC…
阅读更多...
Django API开发实战：前后端分离、Restful风格与DRF序列化器详解

Django API开发实战：前后端分离、Restful风格与DRF序列化器详解

系列文章目录 Django入门全攻略&#xff1a;从零搭建你的第一个Web项目Django ORM入门指南&#xff1a;从概念到实践&#xff0c;掌握模型创建、迁移与视图操作Django ORM实战&#xff1a;模型字段与元选项配置&#xff0c;以及链式过滤与QF查询详解Django ORM深度游&#xff…
阅读更多...
第十五届蓝桥杯大赛 国赛 pb组F题【括号与字母】(15分) 栈的应用

第十五届蓝桥杯大赛 国赛 pb组F题【括号与字母】(15分) 栈的应用

博客主页&#xff1a;誓则盟约系列专栏&#xff1a;IT竞赛 专栏关注博主&#xff0c;后期持续更新系列文章如果有错误感谢请大家批评指出&#xff0c;及时修改感谢大家点赞&#x1f44d;收藏⭐评论✍ 试题F:括号与字母 【问题描述】 给定一个仅包含小写字母和括号的字符串 S …
阅读更多...
【CentOS 7】挑战探索：在CentOS 7上实现Python 3.9的完美部署指南

【CentOS 7】挑战探索：在CentOS 7上实现Python 3.9的完美部署指南

【CentOS 7】挑战探索&#xff1a;在CentOS 7上实现Python 3.9的完美部署指南 大家好 我是寸铁&#x1f44a; 总结了一篇【CentOS 7】挑战探索&#xff1a;在CentOS 7上实现Python 3.9的完美部署指南详细步骤✨ 喜欢的小伙伴可以点点关注 &#x1f49d; 前言 此篇教程只适用于p…
阅读更多...
LeetCode 算法： 旋转图像c++

LeetCode 算法： 旋转图像c++

原题链接&#x1f517;&#xff1a; 旋转图像 难度&#xff1a;中等⭐️⭐️ 题目 给定一个 n n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。 你必须在 原地 旋转图像&#xff0c;这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图…
阅读更多...
OrangePi AIpro小试牛刀-目标检测（YoloV5s）

OrangePi AIpro小试牛刀-目标检测（YoloV5s）

非常高兴参加本次香橙派AI Pro&#xff0c;香橙派联合华为昇腾打造的一款AI推理开发板评测活动&#xff0c;以前使用树莓派Raspberry Pi4B 8G版本&#xff0c;这次有幸使用国产嵌入式开发板。 一窥芳容 这款开发板搭载的芯片是和华为昇腾的Atlas 200I DK A2同款的处理器&#…
阅读更多...
服务器通的远程桌面连接不上，服务器通的远程桌面连接不上解决方法

服务器通的远程桌面连接不上，服务器通的远程桌面连接不上解决方法

当面临服务器远程桌面连接不上的问题时&#xff0c;专业的处理方式需要遵循一系列步骤来确保问题得到准确且高效的解决。以下是一些建议的解决方法&#xff1a; 一、初步排查与诊断 1. 检查网络连接&#xff1a; - 确保本地计算机与服务器之间的网络连接是稳定的。 - 尝…
阅读更多...
【万方数据库爬虫简单开发（自用）】

【万方数据库爬虫简单开发（自用）】

万方数据库爬虫简单开发&#xff08;自用&#xff09;&#xff08;一&#xff09; 使用Python爬虫实现万方数据库论文的搜索并获取信息1.获取url2.输入关键词3.使用BeautifulSoup解析4.获取文章标题信息 使用Python爬虫实现万方数据库论文的搜索并获取信息 后续会逐步探索更新…
阅读更多...
【Mac】Downie 4 for Mac（视频download工具）兼容14系统软件介绍及安装教程

【Mac】Downie 4 for Mac（视频download工具）兼容14系统软件介绍及安装教程

前言 Downie 每周都会更新一个版本适配视频网站&#xff0c;如果遇到视频download不了的情况&#xff0c;请搜索最新版本https://mac.shuiche.cc/search/downie。 注意&#xff1a;Downie Mac特别版不能升级&#xff0c;在设置中找到更新一列&#xff0c;把自动更新和自动downl…
阅读更多...
【数据结构】二叉树：一场关于节点与遍历的艺术之旅

【数据结构】二叉树：一场关于节点与遍历的艺术之旅

专栏引入 哈喽大家好&#xff0c;我是野生的编程萌新&#xff0c;首先感谢大家的观看。数据结构的学习者大多有这样的想法&#xff1a;数据结构很重要&#xff0c;一定要学好&#xff0c;但数据结构比较抽象&#xff0c;有些算法理解起来很困难&#xff0c;学的很累。我想让大家…
阅读更多...
QT中为程序加入超级管理员权限

QT中为程序加入超级管理员权限

QT中为程序加入超级管理员权限 Chapter1 QT中为程序加入超级管理员权限1. mingw编译器2. MSVC编译器3. CMAKE Chapter2 如何给QT程序添加管理员权限(UAC)的几种方法1、Qt Creator中方案一&#xff1a;&#xff08;仅适用于使用msvc编译器&#xff09;方案二&#xff1a;&#x…
阅读更多...
uniapp地图自定义文字和图标

uniapp地图自定义文字和图标

这是我的结构&#xff1a; <map classmap id"map" :latitude"latitude" :longitude"longitude" markertap"handleMarkerClick" :show-location"true" :markers"covers" /> 记住别忘了在data中定义变量…
阅读更多...
【目标检测】基于深度学习的车牌识别管理系统(含UI界面）【python源码+Pyqt5界面 MX_002期】

【目标检测】基于深度学习的车牌识别管理系统(含UI界面）【python源码+Pyqt5界面 MX_002期】

系统简介&#xff1a; 车牌识别技术作为经典的机器视觉任务&#xff0c;具有广泛的应用前景。通过图像处理方法&#xff0c;车牌识别技术能够对车牌上的字符进行检测、定位和识别&#xff0c;从而实现计算机对车牌的智能化管理。在现实生活中&#xff0c;车牌识别系统已在小区停…
阅读更多...
springboot宠物领养管理系统计算机毕业设计源码46534

springboot宠物领养管理系统计算机毕业设计源码46534

摘 要 网络发布信息有其突出的优点&#xff0c;即信息量大&#xff0c;资源丰富&#xff0c;更新速度快等&#xff0c;很符合人们希望以捷、便利的方式获得最多最有效信息的要求。本系统就是一个网上宠物领用的系统&#xff0c;为宠物爱好者提供一个信息发布的平台&#xff0c…
阅读更多...
webshell获取总结（cms获取方法、非cms获取方法、中间件拿Webshell方法）

webshell获取总结（cms获取方法、非cms获取方法、中间件拿Webshell方法）

目录 前期准备&#xff1a; 1、cookices靶场网站搭建&#xff1a; 2、dedecms靶场环境搭建&#xff1a; 获取Webshell方法总结&#xff1a; 一、CMS获取Webshell方法 二、非CMS获取Webshell方法 1、数据库备份获取Webshell 例如&#xff1a; 2、抓包上传获取Webshell 3、…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023