学习资料分析
- 速算运算 √
- 截位直除
- 分数比较
- 等比修正
- 其他速算方法
- 基期与现期
- 基本概念
- 求基期
- 求现期
- 增长率与增长量
- 增长相关统计术语
- 求一般增长率
- 比较一般增长率
- 增长量
- 比重
- 比重相关公式
- 求比重
- 平均数
- 倍数
- 间隔增长
- 乘积增长率
- 年增长率
- 混合增长率
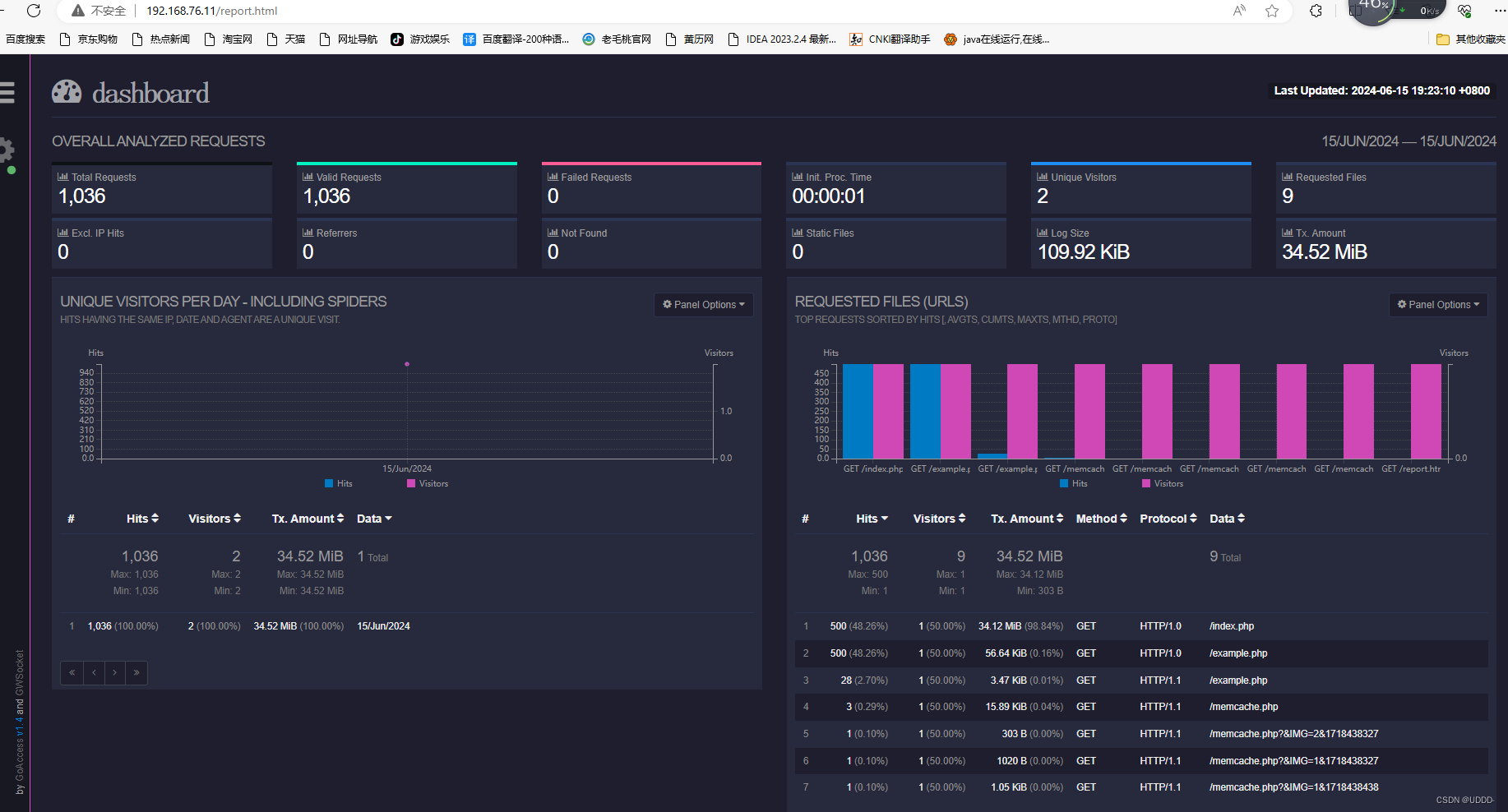
资料分析:主要测查报考者对文字、数字、图表等统计性资料的综合理解与分析加工能力
副省级、地市级、行政执法卷,均考察4篇材料,共4×5=20题
速算运算 √
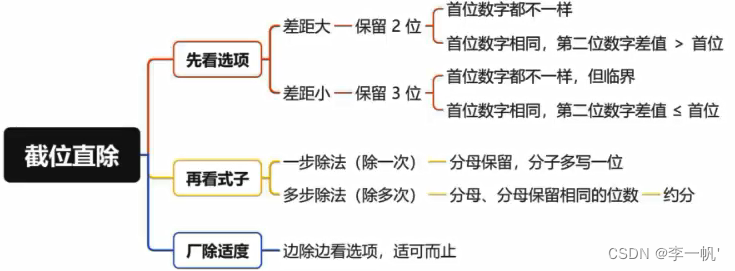
截位直除
-
保留有效数字
-
分母保留几位有效数字 (无脑保留三位,不要全算)
- 选项差距大:保留2位小数,算的快还准
- 首位数字都不一样:A:26 B:36
- 首位数字相同,第二位数字差值大于首位:A:13 B:15 5-3 = 2 > 1
- 选项差距小:保留3位小数,算得慢,但保准
- 首位数字都不一样,但临界:A:29 B:30
- 首位数字相同,第二位数字数字差≤首位:A:207 B:227 2-0 = 2 <= 2
- 四个选项,找最接近的两个,判断差距大小
- 选项差距大:保留2位小数,算的快还准
-
一步除法(除一次): A B 、 A ± B C 、 A B ± C 、 A ± B C ± D \frac A B、\frac {A±B}{C}、\frac{A}{B±C}、\frac{A±B}{C±D} BA、CA±B、B±CA、C±DA±B
- 选项差距大,分母保留2位,分子抄3位(不进位)
- 选项差距小,分母保留3位,分子抄4位(不进位)
-
多步除法(除多次): A B ÷ C 、 A B ÷ C D \frac A B ÷ C、\frac A B÷ \frac C D BA÷C、BA÷DC
- 选项差距大,分母保留2位,分子抄2位(不进位)
- 选项差距小,分母保留3位,分子抄3位(不进位)
-
在除法中,位数、小数点、百分号只会改变结果的位数,不会改变有效数字
-
-
例题
127.38 / 1.4508 ≈
A。61.3 B.73.5 C.87.7 D.101.36064 + 406 / 42462 ≈
A.13% B.15% C.17% D.19%232.8934 / 1 + 12.5 ≈
A.227 B.217 c.207 D.19789591 / 14% ≈
A.200万 B.640万 C.20万 D.64万463536 / 1575.1 + 250.2 ≈
A.2.5 B.2.9 C.3.4 D.4.04774 / 2828 / 1 +10.6%≈
A.1.3 B.1.5 C.1.7 D.1.926352.1 / 32161.9 ÷ 2254.7 / 6946.7 ≈
A.2.5 B.3.6 C.5.3 D.11.7
分数比较
-
同大同小比较
- 竖向直除,分母一般保留2位估算范围(暴力法。位数相同,看有效数字;位数不同,注意位数)
3050 / 47203 3700 / 50251 30 / 47 37 / 50- 横向倍数:看分子间几倍,看分母间几倍(分子间倍数大,只看分子,分子大,分数大;分母间倍数大,只看分母,分母大,分数小)
37 / 24 12 / 9 37 / 27 = 12 * 3+ / 9 * 2+ = 12 / 9 * 3+ / 2+ = 12 / 9 * 1+ > 12 / 9 看 37 / 12 的比值与 24 / 9的比值 24 / 37 9 / 122580 / 3787 5770 / 7557 5770 / 2580 = 2+ 7557 / 3787 = 2- 2+ > 2- 看分子 5770 > 2580 2580 / 3787 > 5770 / 75571024 / 2755 3726 / 11178 -
4个分数比较
-
找参照
- 找最大,以分子最大的分数作参照,与其他分数逐一比较
- 找最小,以分子最小的分数作参照,与其他分数逐一比较
3850 / 40007 3350 / 43852 3050 / 47203 3700 / 50251 -
估范围(大力出奇迹)
- 竖向直除,分母一般保留2位估算范围
- 位数相同,看有效数字;位数不同,注意位数
1442 / 7017 1240 / 5575 1289 / 4335 1386 / 304616.06 / 42.70 8.46 / 49.74 8.22 / 39.54 9.65 / 43.23

-
等比修正
-
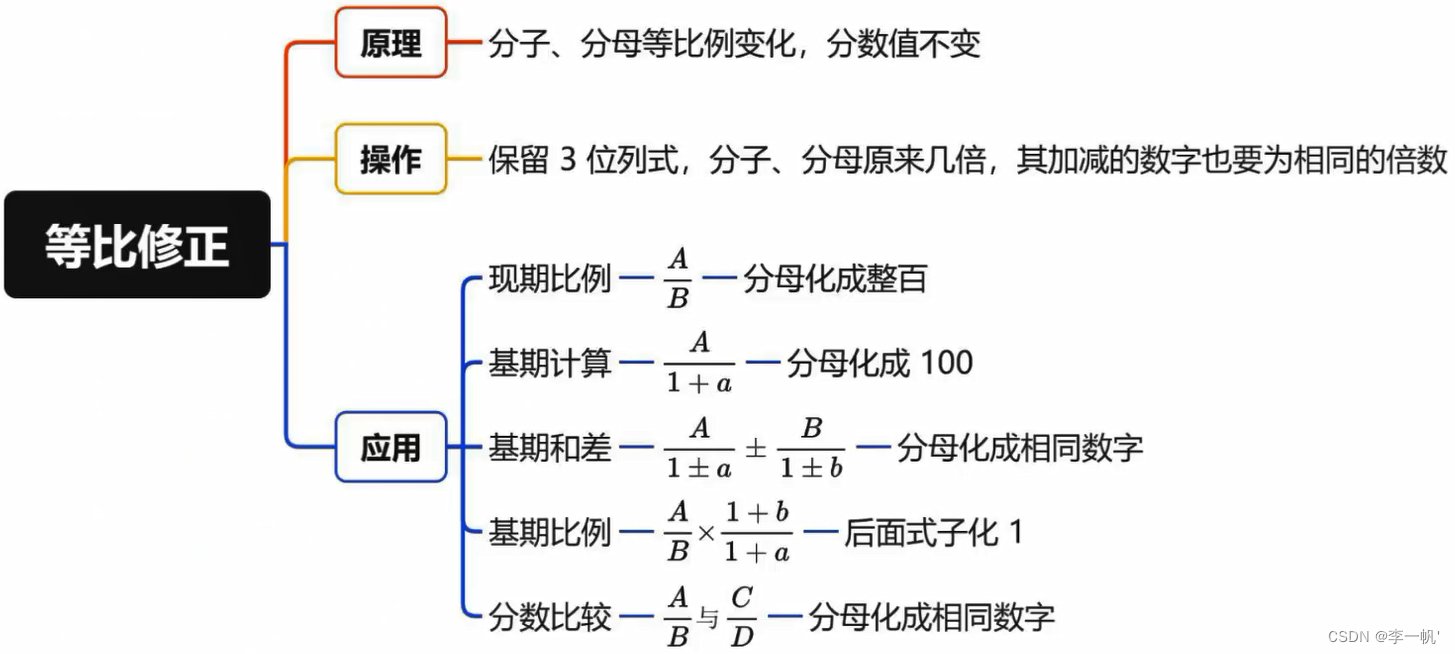
原理:分子、分母等比例变化,分数值不变
-
操作:分子、分母原来几倍,其加减的数字也要为相同的倍数
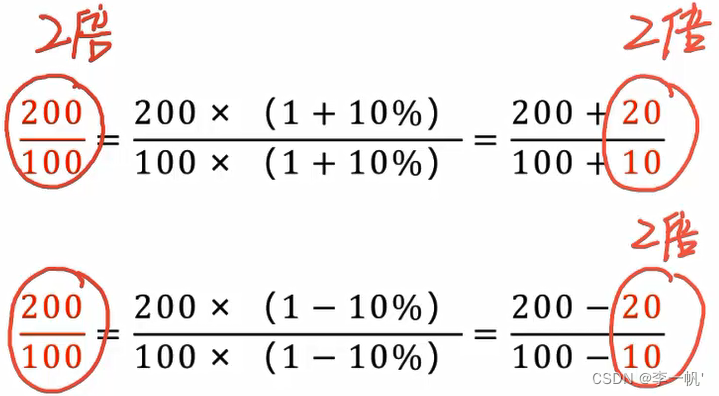
200 / 108 ≈ 200 - 16 / 108 - 8 = 184 / 100 = 1.84
252 / 98 ≈ 252 + 5 / 98 + 2 = 257 / 100 = 2.57
- 应用范围
-
现期比例: A / B
-
基期计算: A / 1+ a
-
基期和差:A / 1 + a ± B / 1 + b
-
基期比例:A/B * 1+b / 1 + a
-
分数比较:使两分数的分母一致
-
其他速算方法
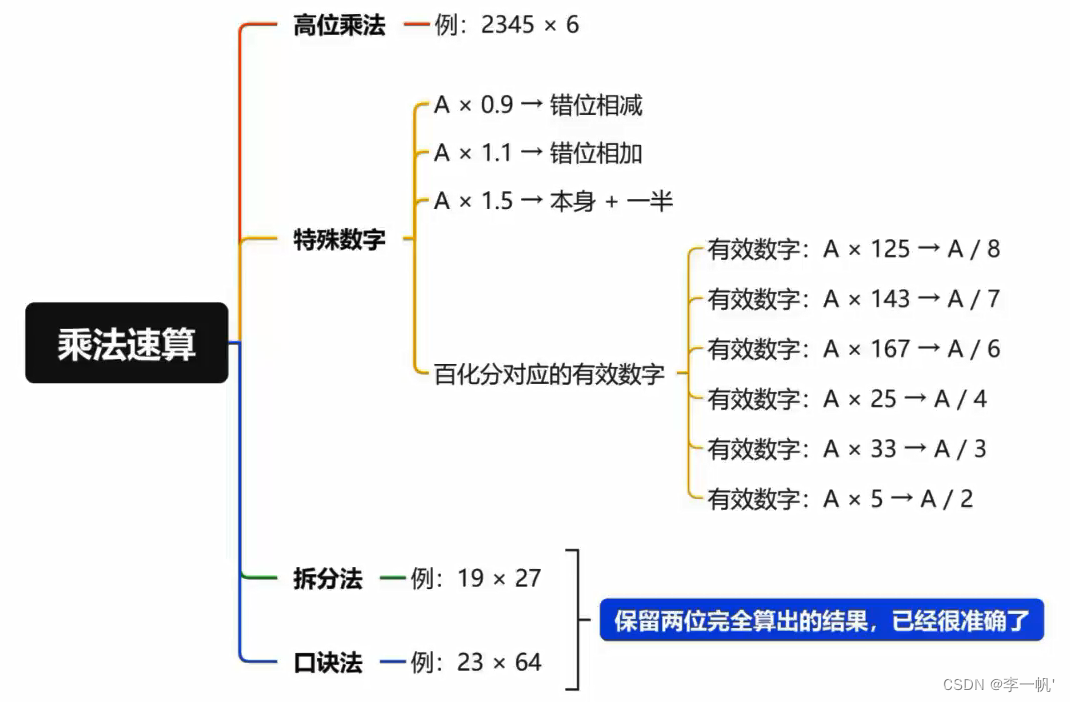
基期与现期
基本概念
- 基期与现期
- 时间型:以过去为参照,衡量现在的发展
- 对象型:比字后面作为参照
- 增长量与增长率
- 同比与环比:同比看头,环比看尾
- 2024年第一季度,同比与2023年第一季度相比,环比与2023年第四季度比
- 2024年2月,同比与2023年2月相比,环比与2024年1月比
求基期
读题看时间,材料给现在,题干求过去
- 基期 = 现期 - 增长量
- 基期 = 增长量 / 增长率
- 基期 = 现期 / (1+增长率)
2022 年1-4 月份,全国房地产开发投资 39154亿元,同比下降2.7%,增速较去年同期回落 5.2 个百分点;其中,住宅投资 29527 亿元,同比下降 2.1%,增速较去年同期回落 7.4 个百分点。
【例 3】(2023 天津事业单位)2021年1-4月,全国房地产开发投资约多少亿元?
A.38541
B.38976
C.39259
D.40240
等比修正应用于基期计算
2019年6月,全国发行地方政府债券8996亿元,同比增长68.37%,环比增长 195.63%。其中,发行一般债券 3178 亿元,同比减少 28.33%,环比增长117.08%,发行专项债券 5818亿元,同比增长 540.04%,环比增长 268.46%。
2019年1至6月,全国发行地方政府债券28372 亿元,同比增长101.09%。其中,发行-般债券 12858 亿元,同比增长 23.21%,发行专项债券 15514 亿元,同比增长322.38%。
【例4】(2020 联考)2018年1至5月,全国发行地方政府债券约:
A.23029 亿元
B.19376 亿元
C.14109 亿元
D.8766 亿元
28372 / 1 + 101.09% - 8996 / 1 + 68.37%通过等比修正将两除式的分母趋同,只变单一一个(不要划两次)截至 2019 年 12 月底,G省移动电话期末用户 1.65 亿户,下降 1.7%;4G期末用户 1.43 亿户,增长 2.3%。互联网宽带接入期末用户 3802万户,增长 2.7%;移动互联网期末用户 1.42 亿户,下降 8.2%。
【拓 展】(2021广东)2018年末,下列G省的电信业务用户数量最多的是:
A.移动电话期末用户
B.4G期末用户
C.互联网宽带接入期末用户
D.移动互联网期末用户
求现期
-
现期识别:读题看时间,材料给现在,题干求以后
-
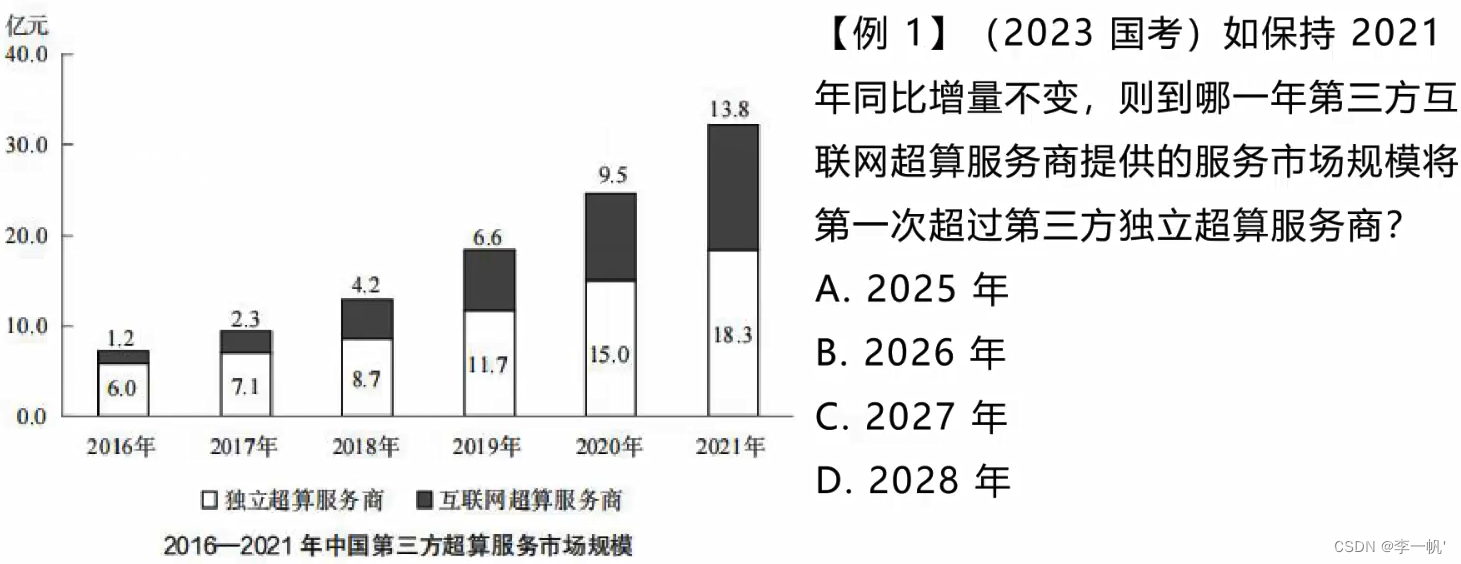
标志性特征:若保持…的增长量/增长率不变…
-
基础公式
- 现期 = 基期 + 增长量
- 现期 = 基期 × (1 + 增长率)
近年来,随着互联网、云计算、大数据以及社交媒体应用的快速发展,我国电子政务也发展迅速。
2018 年我国电子政务市场规模 3106.9亿元,同比2017年的 2861.8亿元增长了 8.6%
【例 2】(2020 广东选调)根据 2018年的增长率预测,2019 年我国电子政务市场
的规模约为多少亿元?
A.3270
B.3370
C.3470
D.3570

高位叠加:两位一估
增长率与增长量
增长相关统计术语
-
倍数与增长率吗
-
倍数:A是B的几倍,A / B
-
增长率:A比B的增长率, A − B B = A B − 1 \frac {A-B} B = \frac A B -1 BA−B=BA−1
-
倍数和增长率的关系:增长率:是几倍 -1;是几倍 = 增长率 + 1
例:2024年、2023 年志哥工资分别为120元、100元, 2024年志哥工资比2023年增长多少(注意分母是之前的,被比较的)
-
-
成数:几成相当于十分之几(百分之几十),3成=30%
- 3成多:30% < X < 40%
- 超过3成:X > 30%
-
番数:翻n翻相等于原来的 2 n 2^n 2n倍,100翻3翻 = 100 * 2^3 = 800
-
百分数与百分点
- 百分数:表示两个量的比例关系:男生300人,全班500人,则男生占全班的300/500 = 60%
- 百分点:表示百分数的变化/差距,用减法计算:男生占比60%,女生占比40%,男生占比比女生占比多60%-40%=20个百分点
-
增幅:就是增长率
- 有正有负:增幅为正代表增长,增幅为负表示减少
- 比较时,有负号带负号
例:A上升10%,B下降20%,C下降30%,D上升20% 增幅低于20%的有A.B.C 增幅最小的是C -
降幅:只有下降时,才能称为降幅;比较时,只看数字(绝对值)
例:A下降10%,B下降20%,C下降30%,D下降40% 降幅超过15%的有B.C.D 降幅最小的是A -
变化幅度:上升、下降均为变化,比较时:只看数字(绝对值)
例:A上升10%,B下降20%,C下降30%,D上升20% 变化幅度超过5%的有4个 变化幅度最大的是C 变化幅度最小的是A
求一般增长率
- 增长率识别:关键词(增长)+比例(百分数、成数、倍数),又名增速、增幅、增长最快/慢
- 公式:增长率= 增长量 / 基期 = 增长量 / (现期 - 增长量) = (现期 - 基期) / 基期
例:2024 年志哥工资的同比增长10%,增速比上年提高了3个百分点2023 年志哥工资的同比增长率为 7%
例:2024 年志哥工资的同比增长10%,增幅比上年降低了3个百分点2023 年志哥工资的同比增长率为 13%
*例:2024 年志哥工资的同比下降10%,降幅比上年扩大了3个百分点2023 年志哥工资的同比增长率为 -7%
*例:2024 年志哥工资的同比下降10%,降幅比上年收窄了3个百分点2023 年志哥工资的同比增长率为 -13%
注意区分:增速、增幅(有负号带负号计算);降幅:只计算数字(绝对值)
比较一般增长率
-
特定增长率:给现期、基期,判断增长率大于某一数值的有几个
- 增长率为整十的数字(10%、20%等)→ 转化为倍数,速算倍数
- 增长率为非整十的数字(2.7%、4%)→ 回归公式,保留3位
-
给现期、基期,比较增长率
- 现期、基期倍数差异明显,比较倍数
- 现期、基期倍数差异不明显,比较增长率(分数比较,用速算技巧)
比较一般增长率这里的核心方法就是通过倍数关系而非增长率的直接计算进行比较!
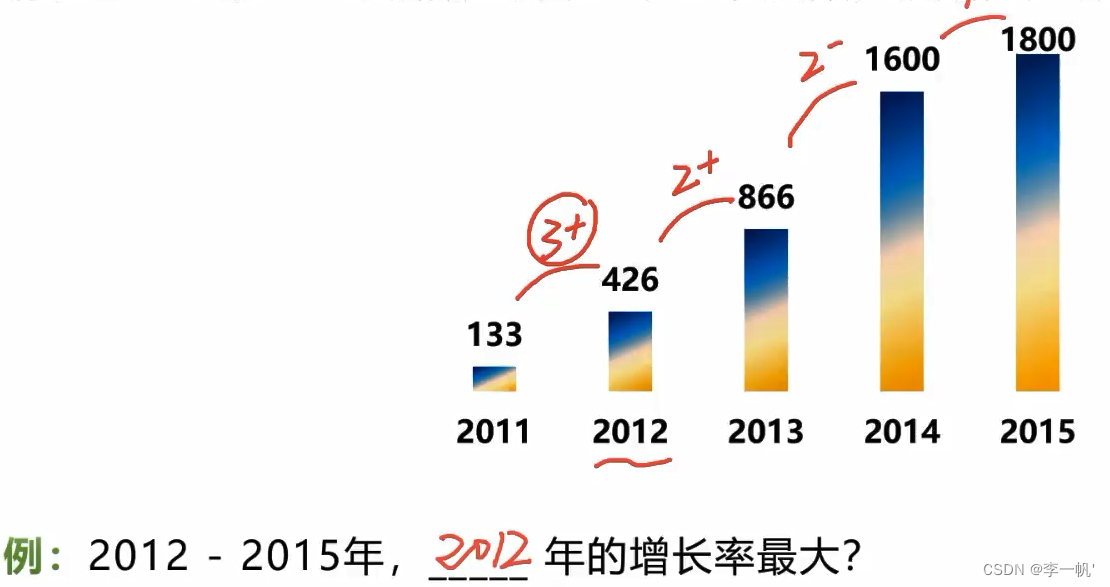
注意2012-2015,这里从2012开始算,另外注意填2012而非2011,通常为后项
- 给现期、增长量,比较增长率
- 公式: 增长率 = 增长量 现期 − 增长量 = 1 现期 增长量 − 1 增长率 = \frac {增长量} {现期-增长量} = \frac 1 {\frac {现期} {增长量} -1} 增长率=现期−增长量