题目列表

3178. 找出 K 秒后拿着球的孩子

3179. K 秒后第 N 个元素的值

3180. 执行操作可获得的最大总奖励 I

3181. 执行操作可获得的最大总奖励 II

一、找出K秒后拿着球的孩子

这题可以直接模拟，从前往后，再从后往前走k次，最后直接返回下标。或者我们可以直接计算，先算出球是从前往后走，还是从后往前走，然后判断球是第几个，返回下标即可，代码如下

//数学
class Solution {
public:int numberOfChild(int n, int k) {int m = k/(n-1), left = k%(n-1); // 因为起始下标是0，所以只要走n-1步就能到最后// m如果是奇数，说明是从后往前，如果是偶数，说明是从前往后return m&1 ? n - left - 1 : left; }
};// 模拟
class Solution {
public:int numberOfChild(int n, int k) {int i = 0, dir = -1;while(k){if(i <= 0|| i >= n-1) dir *= -1;i += dir;k--;}return i;}
};

二、K秒后第N个元素的值

这题可以直接模拟，就是求k次前缀和，返回最后一个元素，也可以直接用数学，去观察它，本质是在求一个组合数C(n+k-1，n-1)，具体过程如下

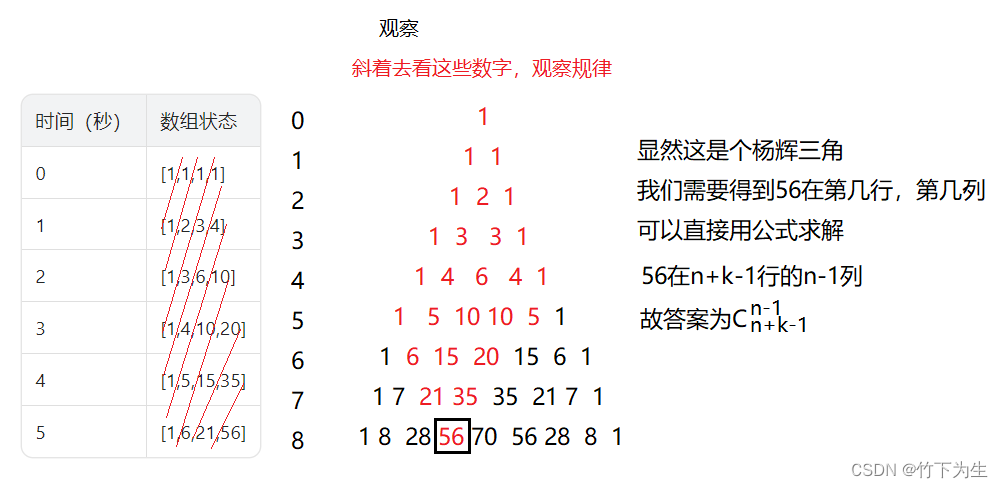
代码如下

// 数学
const int MOD = 1e9+7;
int C[2001][2001]{};
int init=[]()->int{C[0][0] = 1;for(int i = 1; i < 2001; i++){C[i][0] = C[i][i] = 1;for(int j = 1; j <= i/2; j++){C[i][j] = C[i][i-j] = (C[i-1][j] + C[i-1][j-1])%MOD;}}return 0;
}();class Solution {
public:int valueAfterKSeconds(int n, int k) {return C[n+k-1][k];}
};// 模拟
class Solution {const int MOD = 1e9+7;
public:int valueAfterKSeconds(int n, int k) {vector<int> v(n,1);while(k--){for(int i=1;i<n;i++){v[i] = (v[i] + v[i-1])%MOD;}}return v.back();}
};

三、执行操作可获得的最大总奖励 I & II

这题和0-1背包很相似，状态定义为：dp[i][j]表示能否在前i个数中选出一些数使得它们的和为j

状态转移方程为

• 不选nums[i]，dp[i][j] = dp[i-1][j]
• 选nums[i]，dp[i][j] = dp[i-1][j-nums[i]]，其中 0 <= j - nums[i] < nums[i]
• 故dp[i][j] = dp[i-1][j] | dp[i-1][j-nums[i]]

代码如下

class Solution {
public:int maxTotalReward(vector<int>& nums) {sort(nums.begin(),nums.end());nums.erase(unique(nums.begin(),nums.end()),nums.end()); // 无法选择多个相同的数int n = nums.size(), mx = ranges::max(nums);vector<vector<bool>> dp(n+1,vector<bool>(mx*2));dp[0][0] = true;int ans = 0;for(int i = 0; i < n; i++){for(int j = 0; j < 2*nums[i]; j++){ // 当 j >= 2*nums[i] 时，dp[i+1][j] = dp[i][j]，根据递推，它们都是false，没必要更新dp[i+1][j] = dp[i][j];if(j >= nums[i]) dp[i+1][j] = dp[i+1][j] | dp[i][j - nums[i]];}}for(int i=mx*2-1;i>=0;i--)if(dp[n][i])return i;return -1;}
};
// 优化
class Solution {
public:int maxTotalReward(vector<int>& nums) {sort(nums.begin(),nums.end());nums.erase(unique(nums.begin(),nums.end()),nums.end());int n = nums.size(), mx = ranges::max(nums);vector<bool>dp(mx*2);dp[0] =true;int ans = 0;for(int i = 0; i < n; i++){for(int j = nums[i]; j < 2*nums[i]; j++){dp[j] = dp[j] | dp[j - nums[i]];}}for(int i=mx*2-1;i>=0;i--)if(dp[i])return i;return -1;}
};

第四问的数据范围变大，我们还需要对时间复杂度进行优化，如何做？？？

根据上面的代码，我们只要维护一个2*mx大小的bool数组就可以，但是维护true / false其实只需要一个二进制位就能表示，我们可以将数组大小进行压缩，同时，一旦它用二进制来表示，我们的状态转移，就可以用二进制的 | 运算进行，即可以批量的进行，因为整数在cpu上计算时是以32位整型/64位整型进行或运算的，即速度会提升32倍/64倍，代码如下

class Solution {
public:int maxTotalReward(vector<int>& nums) {sort(nums.begin(),nums.end());nums.erase(unique(nums.begin(),nums.end()),nums.end());int n = nums.size(), mx = ranges::max(nums);bitset<100000> f = 1;for(auto v:nums){int shift = f.size() - v;f |= f << shift >> shift << v;}for(int i = mx*2 - 1; i >= 0; i--)if(f.test(i))return i;return -1;}
};