图论（一）之概念介绍与图形#matlab

图论（一）之概念介绍与图形目录

前言

一、图论介绍

二、基本概念

2.1图的概念

2.2图形分类

2.3邻接矩阵

2.3.1无向图

2.3.2有向图

2.3.3有向赋权图

2.4出度（Outdegree）

2.5入度（Indegree）

3.四种图论图形的matlab代码

4.运行结果

5.图论应用

6.算法

总结

前言

图论——这一专注于点和线之间关系的学科，如同一条独特的脉络，将无数看似孤立的领域紧密地连接在一起。

一、图论介绍

从数学建模角度来看，图论（Graph Theory）是数学的一个分支，主要研究由若干给定的点（通常称为顶点或节点）以及连接这些点的线（通常称为边）所构成的图形。这种图形通常用来描述某些事物之间的某种特定关系，其中点代表事物，边表示事物之间具有的关系。

二、基本概念

2.1图的概念

图G通常表示为二元组(V(G),E(G))。公式（1）是非空有限集，称为顶点集，其中元素称为图G的顶点。顶点（或节点、点）是图中的基本元素，用来表示不同的对象、事件或位置。

$V(G)=\{\nu_1,\nu_2,\cdots,\nu_\nu\},$

公式（1）

公式（2）是顶点集V(G)中的无序(无向图)或有序(有向图)的两个元素组合组成的集合，即称为边集，其中元素称为边。边是连接两个顶点的线，表示顶点之间的关系或连接。边可以是有向的（单向关系），也可以是无向的（双向关系）。

$E(G)=\{e_1,e_2,\cdots,e_n\}$

公式（2）

赋权图：若图G=(V(G),E(G))的每一条边e都赋以一个实数w(e)，称w(e)为边e的权，G连同边上的权称为赋权图。

2.2图形分类

所有图论里的图都可以根据是否有向和是否加权分类。

2.3邻接矩阵

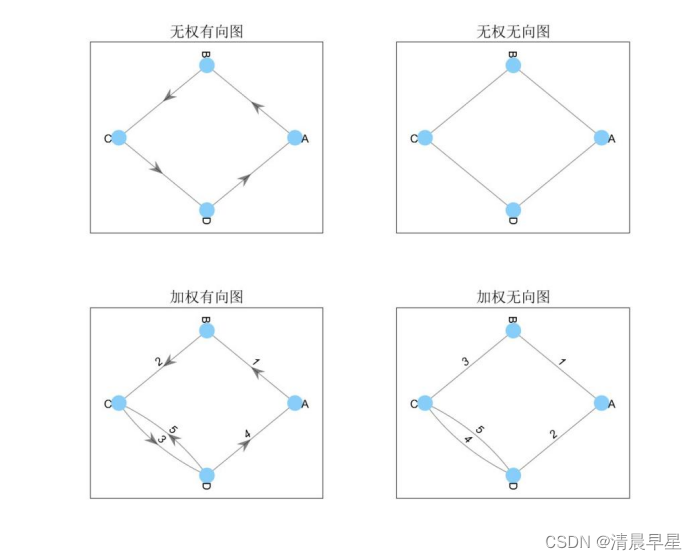
图1 四种图论基本图

2.3.1无向图

根据上图1中的无权无向图可以得出其邻接矩阵为：

2.3.2有向图

根据上图1中的无权有向图可以得出其邻接矩阵为：

2.3.3有向赋权图

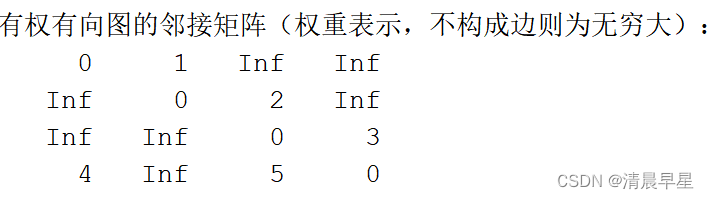
根据上图1中的有权有向图可以得出其邻接矩阵为：

2.4出度（Outdegree）

定义：由某个顶点指出的边的个数称为该顶点的出度；解释：在有向图中，一个顶点的出度表示从这个顶点出发的边的数量；换句话说，这些边都是以该顶点为“尾”（tail），指向其他顶点作为“头”（head）。

示例：在图3中，顶点D指向顶点A和顶点C，那么顶点D的出度就是2。

2.5入度（Indegree）

定义：指向某个顶点的边的个数称为该顶点的入度；解释：在有向图中，一个顶点的入度表示指向这个顶点的边的数量；这些边都是以其他顶点为“尾”，以该顶点为“头”。

3.四种图论图形的matlab代码

clc; clear; 
%% 1. 创建无权的有向图和无向图 
V = {'A', 'B', 'C', 'D'}; 
E = {'A' 'B'; 'B' 'C'; 'C' 'D'; 'D' ,'A'}; 
% 1.1 创建无权有向图 
G_directed = digraph(E(:,1), E(:,2)); 
% 绘制图形 
figure; % 只在这里调用 figure，以创建一个新的图形窗口 
subplot(2,2,1); 
plot(G_directed, 'Layout', 'circle', 'NodeColor', [0.5294 0.8078 0.9804], ... 
'MarkerSize', 10, 'EdgeColor', 'black', 'ArrowSize', 10); 
title('无权有向图'); 
% 获取有向图的邻接矩阵 
adjacency_directed = adjacency(G_directed); 
disp('无权有向图的邻接矩阵：'); 
disp(adjacency_directed);
% 1.2 创建无权无向图 
E = {'A' 'B'; 'B' 'C'; 'C' 'D'; 'D' ,'A'}; 
G_undirected = graph(E(:,1), E(:,2)); 
subplot(2,2,2); 
plot(G_undirected, 'Layout', 'circle', 'NodeColor', [0.5294 0.8078 0.9804], ... 
'MarkerSize', 10, 'EdgeColor', 'black'); 
title('无权无向图'); 
% 获取无向图的邻接矩阵 
adjacency_undirected = adjacency(G_undirected); 
disp('无权无向图的邻接矩阵：'); 
disp(adjacency_undirected);
%% 2. 创建加权的有向和无向图 
weights = [1, 2, 3, 4,5]; % 边的权重 
% 2.1 创建有权有向图 
E = {'A', 'B'; 'B', 'C'; 'C', 'D'; 'D', 'A';'D','C'}; 
G_weighted_directed = digraph(E(:,1), E(:,2), weights); 
subplot(2,2,3); 
plot(G_weighted_directed, 'Layout', 'circle', 'NodeColor', [0.5294 0.8078 0.9804], ... 
'MarkerSize', 10, 'EdgeColor', 'black', 'ArrowSize', 10, 'EdgeLabel', weights); 
title('加权有向图'); 
% 初始化邻接矩阵（全无穷大） 
num_nodes = numel(V); 
adjacency_matrix_weighted_directed = inf(num_nodes, num_nodes); 
% 将对角线元素设置为0（节点到自身的权重为0） 
% 因为这里我们不需要考虑节点到自身的边（通常默认为0或不考虑），所以这步可以省略 
% 但为了保持一致性，我们还是设置它为0 
adjacency_matrix_weighted_directed(logical(eye(num_nodes))) = 0; 
% 填充邻接矩阵的权重 
for i = 1:length(E) 
source_index = find(strcmp(V, E{i, 1}), 1); % 找到源节点在V中的索引 
target_index = find(strcmp(V, E{i, 2}), 1); % 找到目标节点在V中的索引 
adjacency_matrix_weighted_directed(source_index, target_index) = weights(i); 
end 
% 显示邻接矩阵（可选） 
disp('有权有向图的邻接矩阵（权重表示，无边为无穷大）：'); 
disp(adjacency_matrix_weighted_directed);
% 2.2 创建有权无向图 
E = {'A', 'B'; 'B', 'C'; 'C', 'D'; 'D', 'A';'D','C'}; 
G_weighted_undirected = graph(E(:,1), E(:,2), weights); 
subplot(2,2,4); 
plot(G_weighted_undirected, 'Layout', 'circle', 'NodeColor', [0.5294 0.8078 0.9804], ... 
'MarkerSize', 10, 'EdgeColor', 'black', 'EdgeLabel', weights); 
title('加权无向图');