例题一

解法(贪⼼):
贪⼼策略:
我们的任何选择,应该让这个数尽可能快的变成 1 。
对于偶数:只能执⾏除 2 操作,没有什么分析的;
对于奇数:
i. 当 n== 1 的时候,不⽤执⾏任何操作;
ii. 当 n == 3 的时候,变成 1 的最优操作数是 2 ;
iii. 当 (n / 2) % 2 == 0 的时候,那么它的⼆进制表⽰是 ......01 ,最优的⽅式应该选择 -1 ,这样就可以把末尾的 1 ⼲掉,接下来执⾏除法操作,能够更快的变成 1 ;
iv. 当 (n / 2) % 2 == 1 的时候,那么它的⼆进制表⽰是 ......11 ,此时最优的策略应该是 +1 ,这样可以把⼀堆连续的 1 转换成 0 ,更快的变成 1 。

例题二

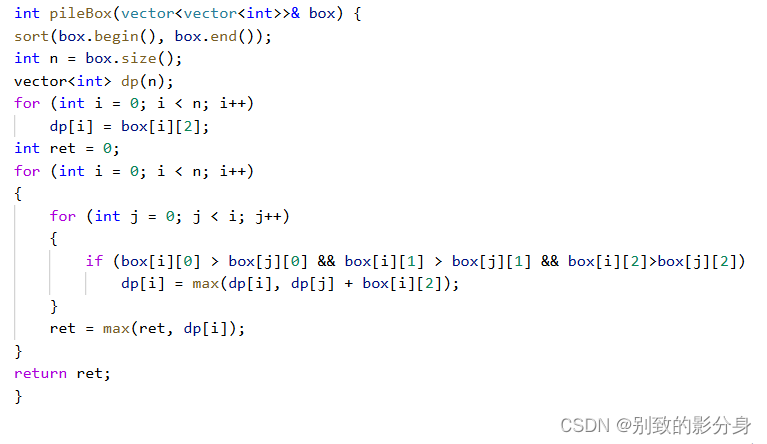
解法⼀(动态规划):
将数组按照左端点排序之后,问题就转化成了最⻓上升⼦序列模型,那接下来我们就可以⽤解决最⻓上升⼦序列的经验,来解决这个问题。
1. 状态表⽰:
dp[i] 表⽰:以 i 位置的箱子为结尾的堆起来的箱子序列中,最高的箱子序列的高度;
2. 状态转移⽅程:
dp[i] = max(dp[i] , dp[j] + box[i] ) 其中 0 <= j < i && box[i][0] > box[j][0] && box[i][1] > box[j][1]&& box[i][2] > box[j][2] ;
3. 初始化:
初始化为 每个箱子原来的高度 ;
4. 填表顺序:
从左往右;
5. 返回值:
整个 dp 表中的最⼤值。
例题三

解法⼀(动态规划):
将数组按照左端点排序之后,问题就转化成了最⻓上升⼦序列模型,那接下来我们就可以⽤解决最⻓上升⼦序列的经验,来解决这个问题(虽然会超时,但是还是要好好写代码)。
1. 状态表⽰:
dp[i] 表⽰:以 i 位置的信封为结尾的所有套娃序列中,最⻓的套娃序列的⻓度;
2. 状态转移⽅程:
dp[i] = max(dp[j] + 1) 其中 0 <= j < i && e[i][0] > e[j][0] && e[i][1] > e[j][1] ;
3. 初始化:
全部初始化为 1 ;
4. 填表顺序:
从左往右;
5. 返回值:
整个 dp 表中的最⼤值。
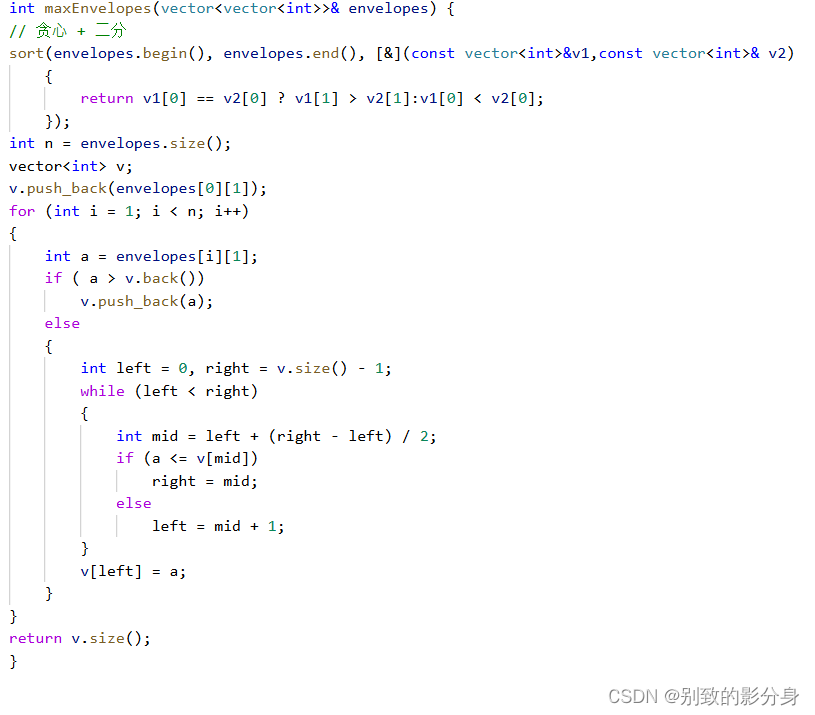
解法⼆(重写排序 + 贪⼼ + ⼆分):
当我们把整个信封按照「下⾯的规则」排序之后:
i. 左端点不同的时候:按照「左端点从⼩到⼤」排序;
ii. 左端点相同的时候:按照「右端点从⼤到⼩」排序;
我们发现,问题就变成了仅考虑信封的「右端点」,完完全全的变成的「最⻓上升⼦序列」的模型。那么我们就可以⽤「贪⼼ + ⼆分」优化我们的算法。
例题四

解法⼀(动态规划):
1. 状态表⽰:
dp[0][i]:表示取到第 i 个数的时候%3余数为0的最大值;
dp[1][i]:表示取到第 i 个数的时候%3余数为1的最大值;
dp[2][i]:表示取到第 i 个数的时候%3余数为2的最大值。
2. 状态转移⽅程:
1.当nums[i-1] % 3 == 0时
dp[0][i] = max(dp[0][i - 1], dp[0][i - 1] + nums[i - 1]);
dp[1][i] = max(dp[1][i - 1], dp[1][i - 1] + nums[i - 1]);
dp[1][i] = max(dp[1][i - 1], dp[1][i - 1] + nums[i - 1]);
dp[2][i] = max(dp[2][i - 1], dp[2][i - 1] + nums[i - 1]);
2.当nums[i - 1] % 3 == 1时
dp[0][i] = max(dp[0][i - 1], dp[2][i - 1] + nums[i - 1]);
dp[1][i] = max(dp[1][i - 1], dp[0][i - 1] + nums[i - 1]);
dp[2][i] = max(dp[2][i - 1], dp[1][i - 1] + nums[i - 1]);
3.当nums[i - 1] % 3 == 2时
dp[0][i] = max(dp[0][i - 1], dp[1][i - 1] + nums[i - 1]);
dp[1][i] = max(dp[1][i - 1], dp[2][i - 1] + nums[i - 1]);
dp[2][i] = max(dp[2][i - 1], dp[0][i - 1] + nums[i - 1]);
3. 初始化:
dp[0][0] = 0, dp[1][0] = INT_MIN, dp[2][0] = INT_MIN;
4. 填表顺序:
从左往右;
5. 返回值:
dp[ 0 ][ n ] 。

解法二(正难则反 + 贪⼼ + 分类讨论):
正难则反:
我们可以先把所有的数累加在⼀起,然后根据累加和的结果,贪⼼的删除⼀些数。
分类讨论:
设累加和为 sum ,⽤ x 标记 %3 == 1 的数,⽤ y 标记 % 3 == 2 的数。那么根据 sum 的余数,可以分为下⾯三种情况:
a. sum % 3 == 0 ,此时所有元素的和就是满⾜要求的,那么我们⼀个也不⽤删除;
b. sum % 3 == 1 ,此时数组中要么存在⼀个 x ,要么存在两个 y 。因为我们要的是最⼤值,所以应该选择 x 中最⼩的那么数,记为 x1 ,或者是 y 中最⼩以及次⼩的两个数,记为y1,y2 。 那么,我们应该选择两种情况下的最⼤值: max(sum - x1, sum - y1 - y2) ;
c. sum % 3 == 2 ,此时数组中要么存在⼀个 y ,要么存在两个 x 。因为我们要的是最⼤值,所以应该选择 y 中最⼩的那么数,记为 y1 ,或者是 x 中最⼩以及次⼩的两个数,记为 x1, x2 。
那么,我们应该选择两种情况下的最⼤值: max(sum - y1, sum - x1 - x2) ;

例题五

解法(贪⼼):
贪⼼策略:
每次处理⼀批相同的数字,往 n 个空⾥⾯摆放;每次摆放的时候,隔⼀个格⼦摆放⼀个数;优先处理出现次数最多的那个数。

例题六

解法(贪⼼):
贪⼼策略:
与上⾯的⼀道题解法⼀致~