我是“导航”
- 1 摘要
- 1.1 简介
- 1.2 问题描述
- 2 超图
- 2.1 图和超图对比
- 参考
1 摘要
1.1 简介
文章提出了一种名为超图神经网络的框架,用于高维数据的表示学习。
该方法英文称呼为 Hypergraph Neural Networks,简写为 HGNN。
1.2 问题描述
- 传统的 GNN 是用于低维数据的表示学习的,没有办法对高维复杂数据进行建模。
- 超图可以对复杂数据进行建模,挖掘数据中的高维关系。
- 但是对超图进行表示学习,这仍没有解决方案。
因此,文章作者提出了 HGNN 方法/框架来解决这一问题。
2 超图
2.1 图和超图对比
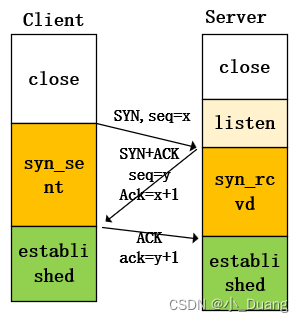
图和超图最大的区别在于:图中边的度为 2,而超图中边的度可以是任意值(原文说了一个词,特别好:degree-free)。

文章中给出了一个示例:

上面部分,是一个图(Graph),下面部分是这个图对应的邻接矩阵(adjacency matrix)。
补充:帮助忘记怎么得到邻接矩阵的小伙伴回忆一下,加深印象。
- 图中的圆圈表示顶点,不同的颜色对不同的顶点加以区分;短线表示边,不同的颜色对不同的边加以区分。图中共有 8 个顶点,记为 { n 1 , n 2 , n 3 , … , n 8 } \{n_1,n_2,n_3, \dots, n_8\} {n1,n2,n3,…,n8};共有 6 条边。
- 每个顶点,如 n 1 n_1 n1,可以连接其他 7 个顶点以及自身,共 8 个顶点。将顶点 n 1 n_1 n1 连接其他顶点的情况排成一行,那么 8 个顶点连接情况就是 8 行,因此就组成了 8 行 8 列的矩阵(8*8)。
- 如果顶点 n i n_i ni 和顶点 n j n_j nj 相连,那么邻接矩阵的第 i i i 行第 j j j 列位置 ( i , j ) (i, j) (i,j) 上的元素值应该为 1;否则为 0。(前提:所有的顶点按顺序排列。)
- 这个矩阵的第一行第一个元素表示顶点 n 1 n_1 n1 连接顶点 n 1 n_1 n1 的情况,第一行的第二个元素表示顶点 n 1 n_1 n1 连接顶点 n 2 n_2 n2 的情况;其余的以此类推。
- 观察图, n 1 n_1 n1(蓝色)连接了 n 5 n_5 n5(灰色)和 n 6 n_6 n6(青色),因此第一行的第五个元素、第六个元素值应该为 1,第一行的其他位置元素值为 0。矩阵的其他位置的值,采取同样的策略赋值。
- 对于无向图,邻接矩阵是对称的;对于有向图,邻接矩阵一般不对称。

原文中说有多组超边(Hyperedge group 1/2/3/…/N),我理解的应该多种输入数据的形式。
观察上面这个超图,顶点和上面图中的顶点,是一模一样的。常用 V V V 表示顶点集合,由此 V = { n 1 , n 2 , … , n 8 } V=\{n_1,n_2,\dots, n_8\} V={n1,n2,…,n8}。超边和图中的边就稍微有些不同了。上面提到,图中有 6 条边,颜色对边进行了区分。超图这里也是用颜色对超边进行了区分。
补充:作者牛逼。这图的审美,真的太棒了。
好了,话说回来,不同的超边使用了不同的颜色。超图中有三种颜色的超边,黑色、红色、深绿色,分别用符号 e 1 e_1 e1、 e 2 e_2 e2、 e 3 e_3 e3 来表示。
构建关联矩阵(incidence matrix):行表示顶点,8 个顶点, n 1 n_1 n1、 n 2 n_2 n2、 … \dots …、 n 8 n_8 n8;列表示超边,3 条超边, e 1 e_1 e1、 e 2 e_2 e2、 e 3 e_3 e3。如果某一个顶点属于某一条超边,则关联矩阵对应位置的值为 1;否则为 0。
- 超边 e 1 e_1 e1 包含顶点 n 2 n_2 n2、 n 4 n_4 n4、 n 8 n_8 n8,所以 ( n 2 , e 1 ) (n_2, e_1) (n2,e1)、 ( n 4 , e 1 ) (n_4, e_1) (n4,e1)、 ( n 8 , e 1 ) (n_8, e_1) (n8,e1) 位置上的值为 1, e 1 e_1 e1 列其他位置上的值为 0。
- 超边 e 2 e_2 e2 包含顶点 n 1 n_1 n1、 n 6 n_6 n6、 n 7 n_7 n7,所以 ( n 1 , e 2 ) (n_1, e_2) (n1,e2)、 ( n 6 , e 2 ) (n_6, e_2) (n6,e2)、 ( n 7 , e 2 ) (n_7, e_2) (n7,e2) 位置上的值为 1, e 2 e_2 e2 列其他位置上的值为 0。
- 超边 e 3 e_3 e3 包含顶点 n 3 n_3 n3、 n 5 n_5 n5、 n 7 n_7 n7,所以 ( n 3 , e 3 ) (n_3, e_3) (n3,e3)、 ( n 5 , e 3 ) (n_5, e_3) (n5,e3)、 ( n 7 , e 3 ) (n_7, e_3) (n7,e3) 位置上的值为 1, e 3 e_3 e3 列其他位置上的值为 0。
- 不知道大家发现没有,顶点 n 7 n_7 n7 在两条超边 e 2 e_2 e2、 e 3 e_3 e3 都存在。

同理,可以得到第 N N N 种数据形式下的关联矩阵 H N H_N HN。

然后将这 N N N 个关联矩阵 { H 1 , H 2 , … , H N } \{H_1, H_2, \dots, H_N\} {H1,H2,…,HN} 拼接起来,得到了最后的 H H H。也即是说:
H = ⋃ i = 1 N H i . H = \bigcup^N_{i=1} H_i. H=i=1⋃NHi.
解读:一般的数据超图只有一个,也即是说只有一个 H H H。而论文中提到了 N N N 个 H i H_i Hi 进行拼接得到一个 H H H,应该是为了更好地利用多模态的数据。即考虑了多种数据的形式。
参考
- Y. Feng, H. You, Z. Zhang, R. Ji et.al. Hypergraph neural networks. In Proceedings of the AAAI conference on artificial intelligence, 2019 (Vol. 33, No. 01, pp. 3558-3565).