---

0.常见的搜索结构

种类	数据格式	时间复杂度
顺序查找	无要求	$O(N)$
二分查找	有序	$O(lo{g}_{2}N)$
二叉搜索树	无要求	$O(N)$
二叉平衡树	无要求	$O(lo{g}_{2}N)$
哈希	无要求	$O(1)$

• 以上结构适合用于数据量相对不是很大，能够一次性存放在内存中，进行数据查找的场景

  • 如果数据量很大，比如有100G数据，无法一次放进内存中，那就只能放在磁盘上了

• 如果放在磁盘上，又需要搜索某些数据，那么如何处理呢？

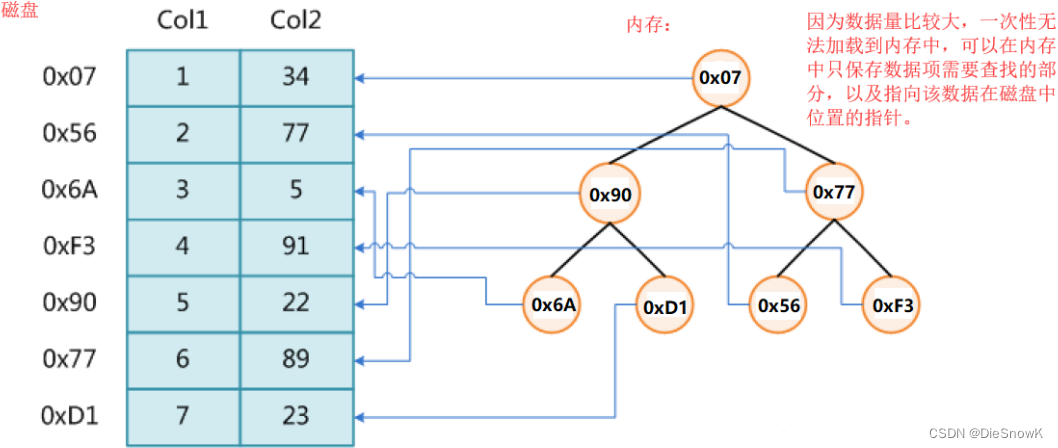
  • 可以考虑将存放关键字及其映射的数据的地址放到一个内存中的搜索树的节点中

  • 要访问数据时，先取这个地址去磁盘访问数据

    

• 使用平衡二叉树的缺陷：

  • 平衡二叉树搜索树的高度是$lo{g}_{2}N$，这个查找次数在内存中是很快的
  • 但是当数据都在磁盘中时，访问磁盘速度很慢
    • 在数据量很大时，$lo{g}_{2}N$次的磁盘访问，是一个难以接受的结果

• 使用哈希表的缺陷：

  • 哈希表的效率很高是$O(1)$
  • 但是一些极端场景下某个位置冲突很多，导致访问次数剧增，也是难以接受的
    • 极端场景下冲突非常严重，效率下降很多

• 那如何加速对数据的访问呢？

  1. 提高IO的速度(SSD相比传统机械硬盘快了不少，但是还是没有得到本质性的提升)
  2. 降低树的高度 – 多叉树平衡树

• 为什么硬盘IO慢？
  

---

1.B树概念

• B树是一种适合外查找的树，它是一种平衡的多叉树
  • 后面有一个改进版本B+树
• 一棵m阶(m>2)的B树，是一棵平衡的M路平衡搜索树，可以是空树或者满足以下性质：
  • 根节点至少有两个孩子
  • 每个分支结点都包含k-1个关键字和k个孩子，其中$ceil(m/2)<=k<=m$
    • 孩子比关键字保持多一个的关系
    • TIPS：ceil()是向上取整函数
  • 每个叶子结点都包含k-1个关键字，其中$ceil(m/2)<=k<=m$
  • 所有的叶子结点都在同一层
  • 每个结点中的关键字从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域划分
  • 每个结点的结构为：$(n，A_0，K_1，A_1，K_2，A_2，\dots ，K_n，A_n)$
    • $K_i(1\le i\le n)$为关键字，且$K_i<K_{i+1}(1\le i\le n-1)$
    • $A_i(0\le i\le n)$为**指向子树根结点的指针**，且$A_i$所指子树所有结点中的关键字均小于$K_{i+1}$
    • n为结点中关键字的个数，满足$ceil(m/2)-1\le n\le m-1$
• B树的性质保证了B树是天然平衡的
  • 只会向右和向上生长
    • 只有在根结点分裂时，才会增加一层
  • 新插入的结点，一定是在叶子插入
    • 叶子没有孩子，不影响关键字和孩子的关系
  • 叶子节点满了，分裂出一个兄弟，提取中位数，向父亲插入一个值和一个孩子

---

2.B-树的插入分析

1.流程分析

• 为了简单起见，假设$M=3$，即三叉树，每个节点中存储两个数据，两个数据可以将区间分割成三个部分，因此节点应该有三个孩子，为了后续实现简单起见，节点的结构如下

  • 注意：孩子永远比数据多一个

    

• 用序列{53, 139, 75, 49, 145, 36, 101}构建B树的过程如下：

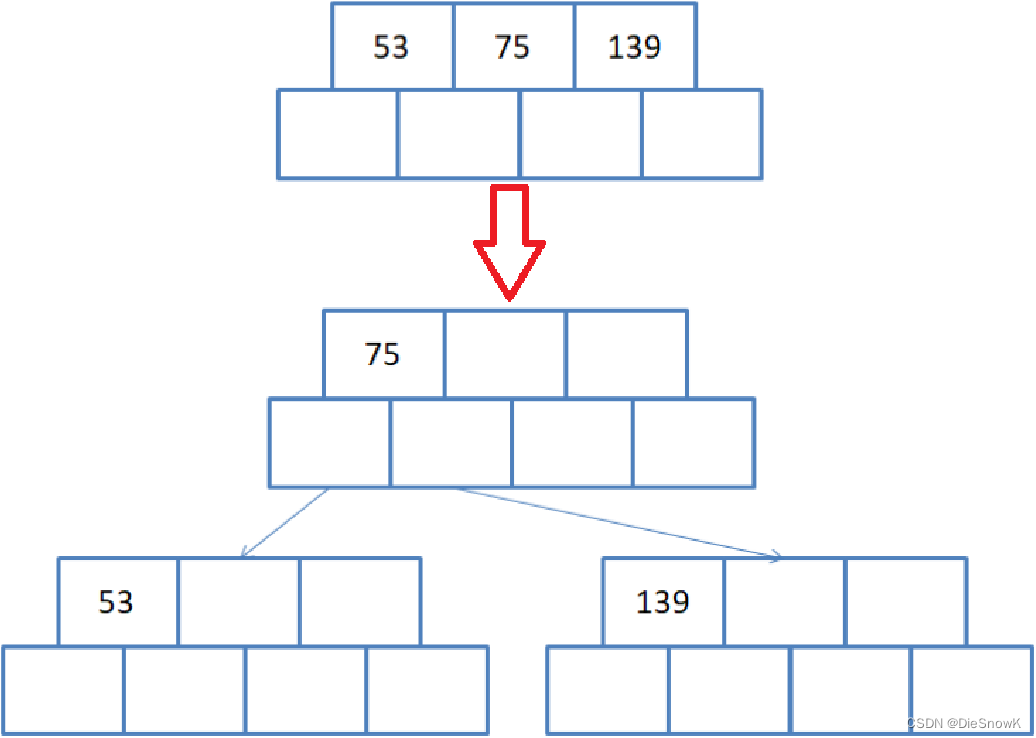
• 插入75的过程如下

  1. 按照插入排序思想，将75插入到序列中

  2. 插入后该结点不满足情况，需要对该结点进行分裂

     

• 分裂结点：关键字的数量等于M，则满了，满了就分裂出一个兄弟结点，分裂一半的值和孩子给兄弟

  1. 找到结点数据域的中间位置
  2. 给一个新结点，将中间位置的右边数据搬移到新结点中
  3. 将中间位置数据搬移到父结点中
  4. 将结点连接好
     

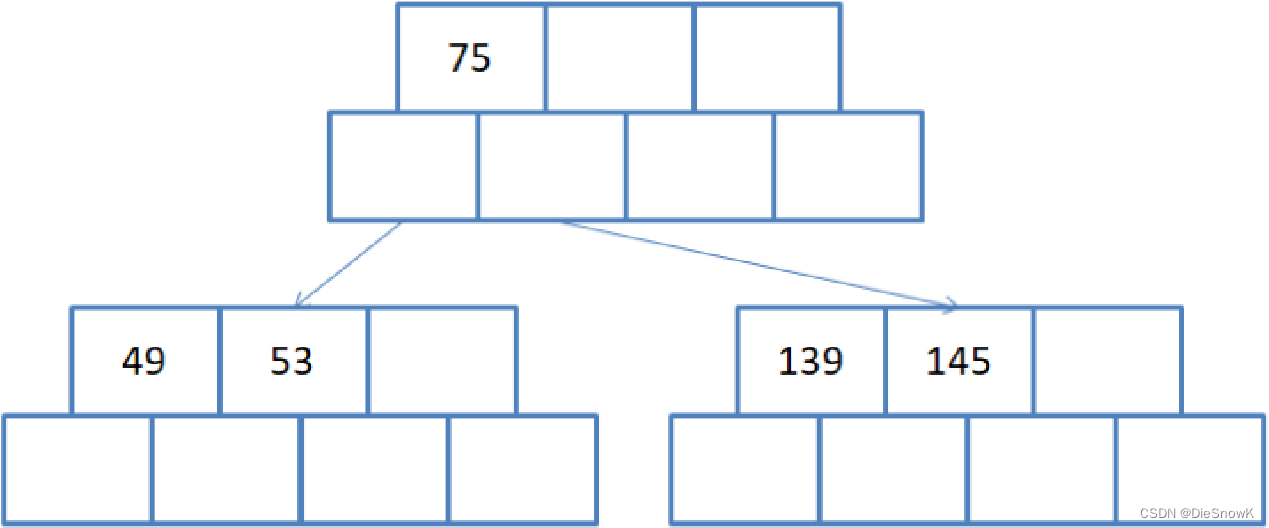
• 插入49，145的过程如下

  1. 找到该元素的插入位置(索要插入结点pCur)
  2. 按照插入排序思想将结点插入到该结点(pcur)的合适位置
  3. 检测该结点是否满足B树的性质
     • 满足：插入结束
     • 不满足：对该结点进行分裂
       

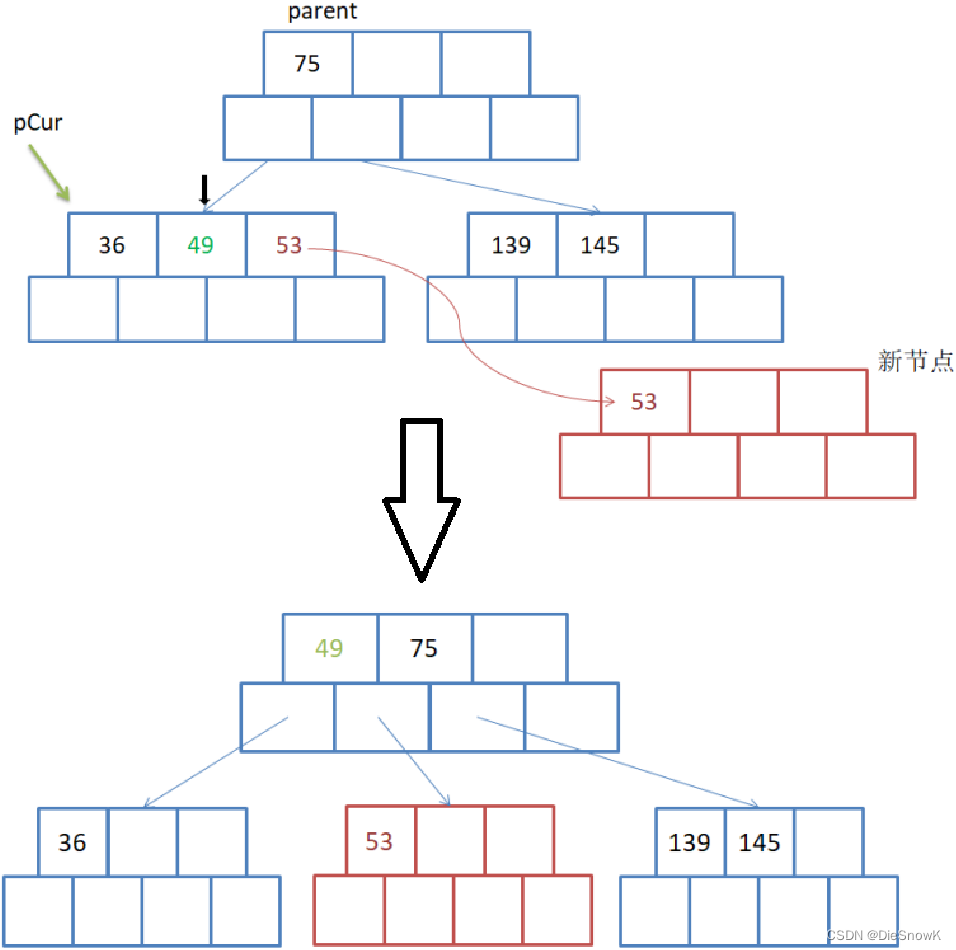
• 插入36的过程如下

  • 插入完成后，该结点违反B-树性质，需要对pCur进行分裂

    1. 找到中间位置

    2. 将中间位置右侧元素搬移到新结点中

    3. 将中间位置数据49以及新生成的结点往parent中继续插入

       

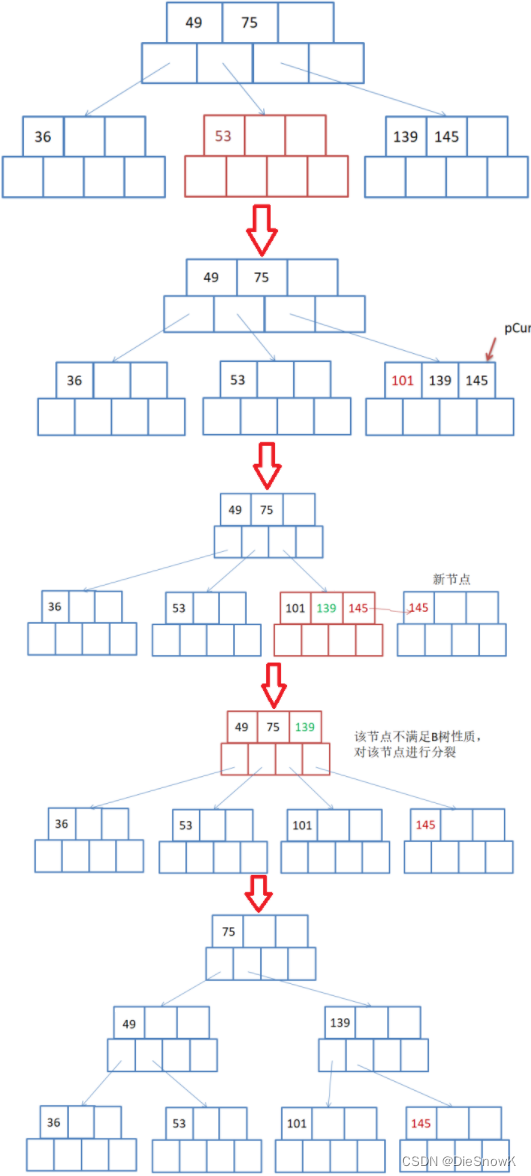
• 插入101的过程如下：

  1. 先在B-树种找到该结点的插入位置
  2. 按照插入排序思想将该结点插入到pCur结点中
  3. 检测该结点是否满足B树的性质，该结点中存放元素个数是否小于M
     • 小于M：插入完成
     • 等于M：需要对该结点进行分裂

       • 找中间位置，将中间位置右侧数据搬移到新结点中

       • 将中间位置数据以及新结点往pCur双亲中继续插入

         

2.插入过程总结

1. 如果树为空，直接插入新节点中，该节点为树的根节点
2. 树非空，找待插入元素在树中的插入位置
   • 注意：找到的插入节点位置一定在叶子节点中
3. 检测是否找到插入位置
   • 假设树中的key唯一，即该元素已经存在时则不插入
4. 按照插入排序的思想将该元素插入到找到的节点中
5. 检测该节点是否满足B-树的性质
   • 即：该节点中的元素个数是否等于M，如果小于则满足
6. 如果插入后节点不满足B树的性质，需要对该节点进行分裂：
   • 申请新节点
   • 找到该节点的中间位置
   • 将该节点中间位置右侧的元素以及其孩子搬移到新节点中
   • 将中间位置元素以及新节点往该节点的双亲节点中插入，即继续(4)
7. 如果向上已经分裂到根节点的位置，插入结束