目录

一、哈夫曼树

1.1基本概念

1.2构造方法

1.3构造算法的实现

二、哈夫曼树的应用

2.1哈夫曼编码

2.2文件的编码和解码

2.2.1编码

2.2.2解码

---

一、哈夫曼树

1.1基本概念

哈夫曼树又称为最优树，是一类带权路径长度最短的树。

最优二叉树：带权路径长度最短(WPL)的二叉树。

①路径：从树中一个结点到另一个结点之间的分支构成这两个结点间的路径。

②结点的路径长度：两节点路径上的分支数。

③树的路径长度：从树根到每一个结点的路径长度之和。

结点数目相同的二叉树中，完全二叉树是路径长度最短的二叉树，但路径长度最短的二叉树不一定是完全二叉树。

④权：将树中结点赋给一个有着某种含义的数值。

⑤结点的带权路径长度：从根结点到该结点之间的路径长度与该结点的权的乘积。

⑥树的带权路径长度(WPL)：树中所有叶子结点的带权路径长度之和。

注：满二叉树不一定是哈夫曼树；

哈夫曼树中权越大的叶子离根越近；

具有相同带权结点的哈夫曼树不唯一。

1.2构造方法

 

·包含n棵树的森林要经过n-1次合并才能形成哈夫曼树，共产生n-1个新结点，结点度数为0或2，没有度为1的结点。

·包含n个叶子结点的哈夫曼树中共有2n-1个结点。

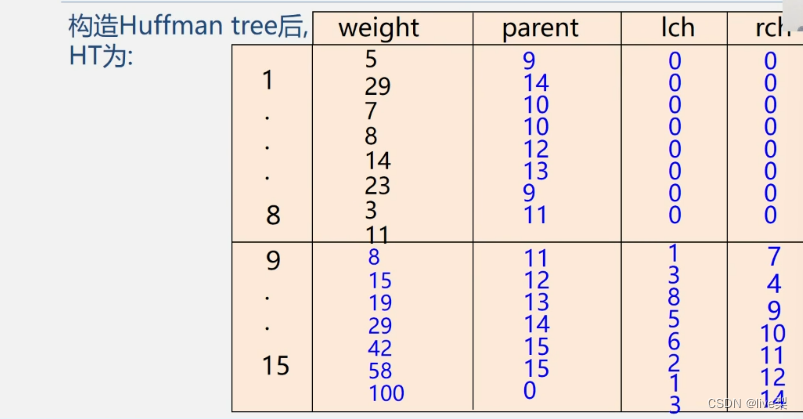
例：

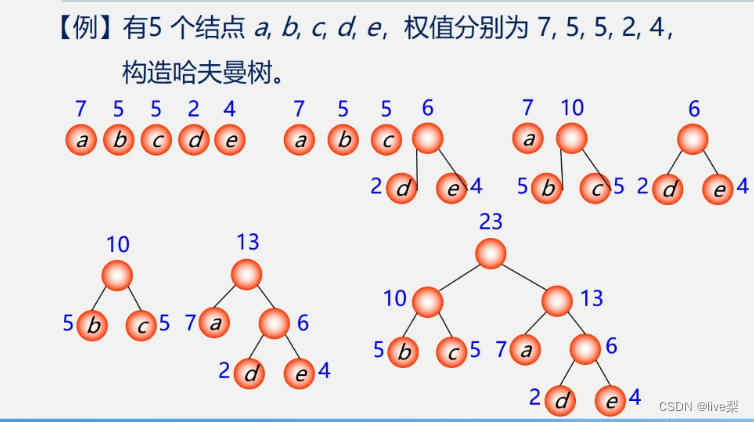
1.3构造算法的实现

采用顺序存储结构

（一维数组）

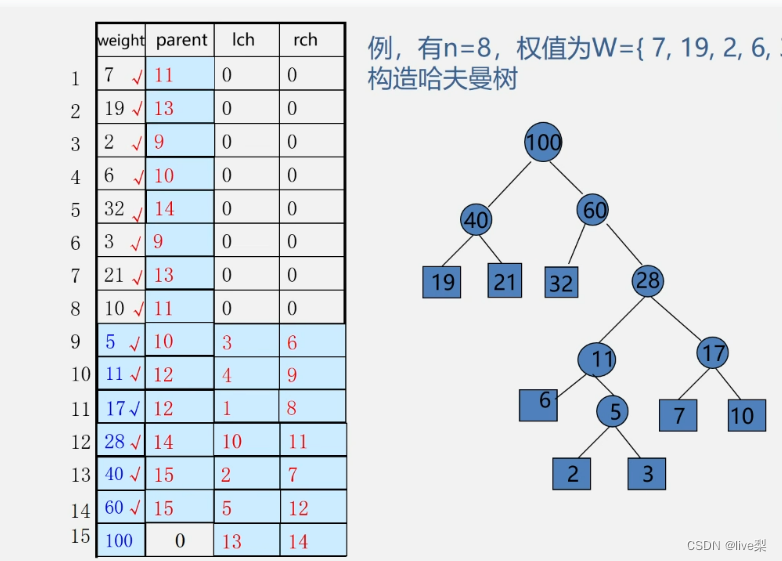
算法实现：

例：

二、哈夫曼树的应用

2.1哈夫曼编码

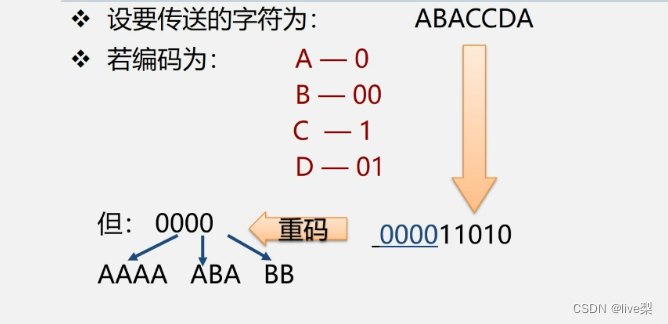
出现了重码情况，改进：使用前缀编码——要设计长度不等的编码，则必须使任一字符的编码都不是另一个字符的编码的前缀

实现：

①出现的概率越大，要求编码越短

②将每个字符的概率值作为权值，构造哈夫曼树

③在哈夫曼树的左分支上标0，右分支上标1

④把从根到每个叶子的路径上的标号连接起来，作为该叶子代表的字符的编码

例：

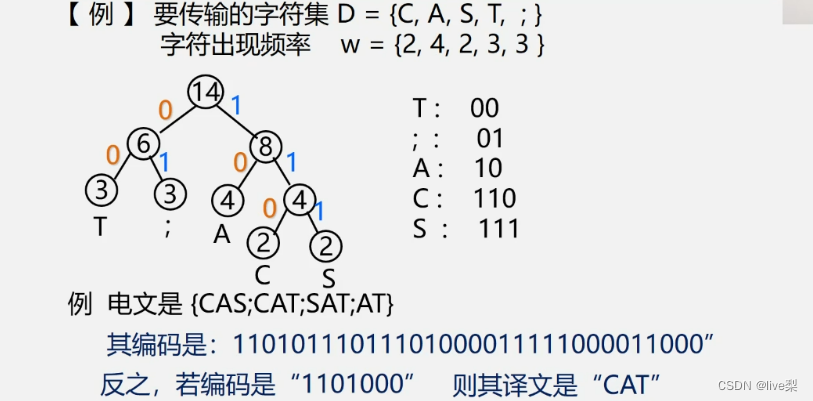
哈夫曼编码是前缀码，是最优前缀码。

算法：

2.2文件的编码和解码

2.2.1编码

①输入各字符及其权值

②构造哈夫曼树——HT[i]

③进行哈夫曼编码——HC[i]

④查HC[i]，得到各字符的哈夫曼编码

2.2.2解码

①构造哈夫曼树

②依次读入二进制码

③读入0，走向左孩子；读入1，走向右孩子

④一旦到达某叶子时，即可译出字符

⑤然后再从根出发继续译码，直到结束

例：