目录

1 算法原理

1.1 优化模型离散方式

1.1.1  Temporal Parameter Discretization

1.2 优化问题建模

1.2.1 Cost function

1.2.2 Constraints

2 ST-Graph

3 代码实现

​编辑

3.1 STBoundsDecider

---

1 算法原理

1.1 优化模型离散方式

在处理最优化问题时，一般会转化成离散形式，将轨迹 s(t) 按照某参数离散，并计算离散点处的约束和 Cost。对于速度规划问题，一般可以按照等间距离散（Spatial Parameter Discretization）和等时间离散（Temporal Parameter Discretization）。

1.1.1  Temporal Parameter Discretization

优点：

缺点：

这条这样理解：

处理方法：

此外，Apollo 还设计了非线性速度规划（就是使用 IPOPT）来处理以上问题。

1.2 优化问题建模

1.2.1 Cost function

其中：

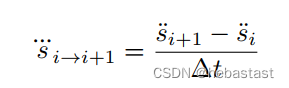
1.2.2 Constraints

1）不等式约束

对上面的约束的解释：

2）等式约束

2 ST-Graph

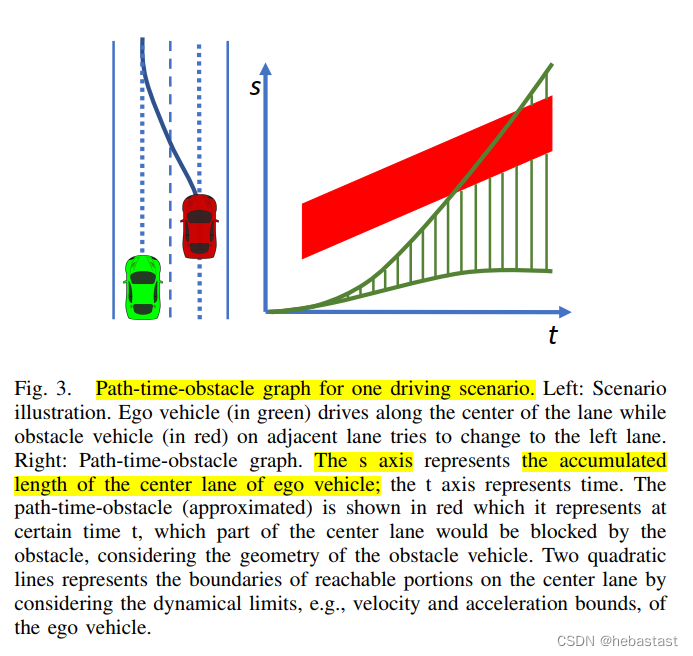
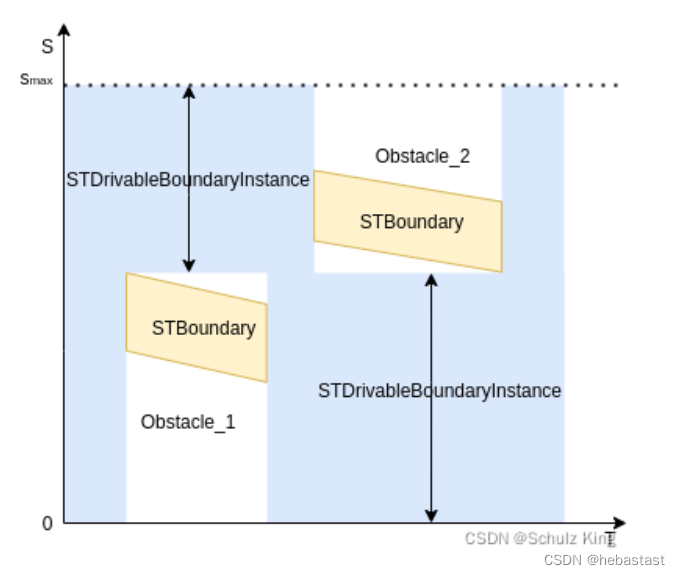
3 代码实现

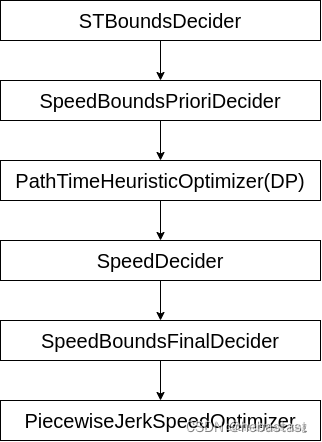
在 Apollo 中速度决策规划的实现流程如下：

3.1 STBoundsDecider

3.1.1 由车辆动力学约束计算得到的行驶范围约束（s_min, s_max）

其计算依据为车辆运动学公式：

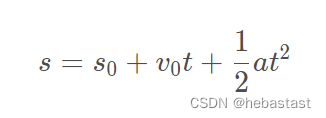
3.1.2 由参考速度计算得到的行驶范围约束

3.1.3 由障碍物计算得到的行驶范围约束

3.2 SpeedBoundsPrioriDecider

3.3 PathTimeHeuristicOptimizer

3.4 SpeedDecider

3.5 SpeedBoundsFinalDecider

3.6 PiecewiseJerkSpeedOptimizer

速度规划的优化求解即是按照上述的算法原理实现的。可以看到，在此会依据纵向决策结果生成纵向位移的约束边界，将每个时刻和 cruise speed 的误差作为优化目标的一部分，并且根据 DP 结果在每个时刻处位移的速度约束作为优化问题的速度约束边界，因此将每个时刻的位移和 DP 的位置之差作为了优化目标的一部分，但是这样只能实现速度的软约束。