一、朴素贝叶斯算法:
朴素贝叶斯算法,是一种基于贝叶斯定理与特征条件独立假设的分类方法,基于贝叶斯后验概率建立的模型,它用于解决分类问题。朴素:特征条件独立;贝叶斯:基于贝叶斯定理。属于监督学习的生成模型,实现简单,并有坚实的数学理论(即贝叶斯定理)作为支撑。在大量样本下会有较好的表现,不适用于输入向量的特征条件有关联的场景。
它的主要思想是,通过历史数据,对每个类别建立经验概率公式,然后当新样本进来时,用各个类别的概率经验公式分别进行预测,最终,属于哪个类别的概率最大,就认为是哪个类别。
二、计算条件概率
朴素贝叶斯算法的核心内容即使贝叶斯公式,也就是计算特征在类别下的条件概率的计算,贝叶斯原理为,在已知发生B条件下,发生A的概率为:
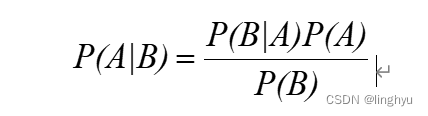
P(A):为先验概率,即在B事件发生之前,对A事件发生概率的预判。
P(A|B):为后验概率,即在B事件发生之后,对A事件发生概率的重新评估。
P(B|A)/P(B):为可能性函数,是一个调整因子,使得预估概率更加接近真实概率。可以理解为:P(B)⋅P(A∣B) = P(B∣A)⋅P(A),即:发生B,且发生A = 发生A且发生B。
换个表达形式就会明朗很多,如下:
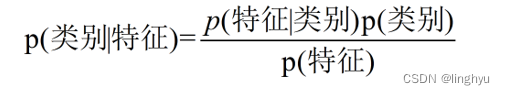
所以贝叶斯公式可以表示为:后验概率=先验概率 * 调整因子
三、预测精度的计算与评估
estimator.score():一般最常见使用的是准确率,即预测结果正确的百分比。

也可以使用召回率(Recall),真实为正例的样本中预测结果为正例的比例(查的全,对正样本的区分能力)

其他分类标准,F1-score,反映了模型的稳健型,F1值是准确率和召回率的调和平均数。
也可以使用分类模型评估API: sklearn.metrics.classification_report
sklearn.metrics.classification_report(y_true,y_pred,target_names=None)
y_true:真实目标值
y_pred:估计器预测目标值
target_names:目标类别名称
return:每个类别精确率与召回率
四、编程实现贝叶斯分类算法,并对简单应用样本数据实现预测分类
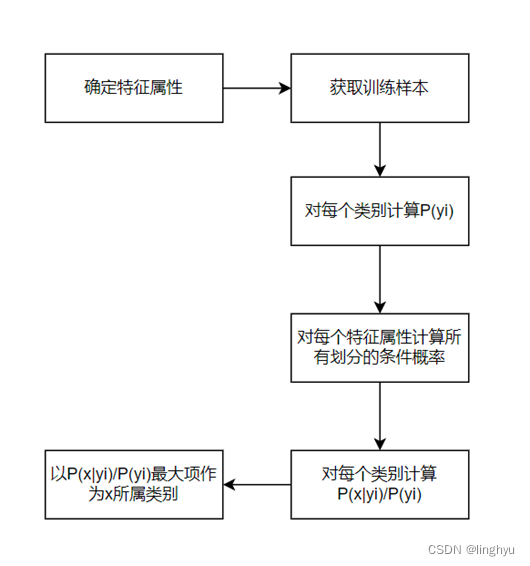
算法过程描述:

我们以西瓜的特征为变量,好坏质量为二元结果,准备数据如下:
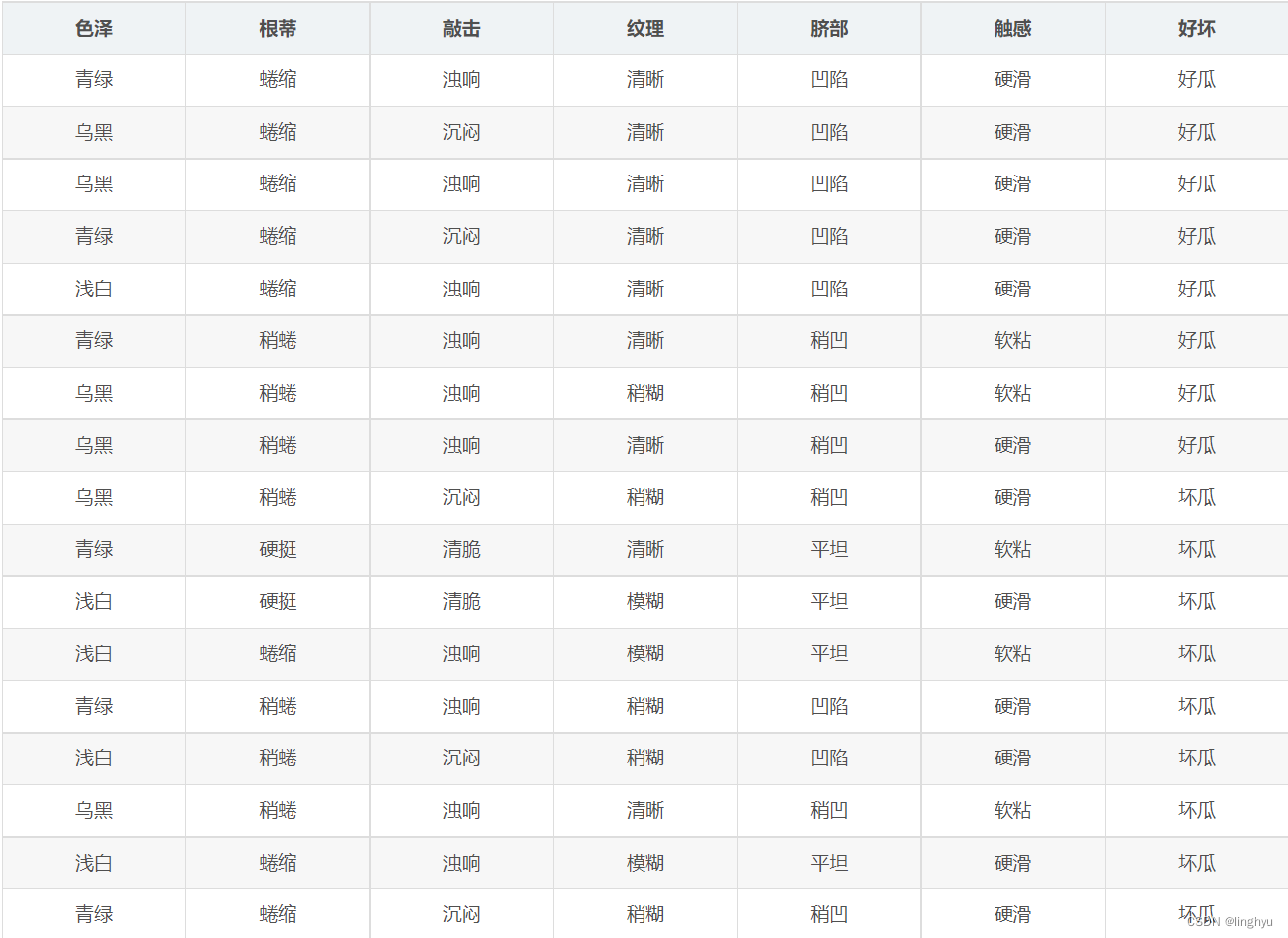
定义一个名数组进行数据集的存储。数据集的每一行表示一个西瓜的属性,包括色泽、根蒂、敲击、纹理、脐部和触感。最后一行表示西瓜是好瓜还是坏瓜。
并且申请一个字典存放特征features(特征)的可能值,并为最终的二元结果申请一个列表标签 labels(标签)。
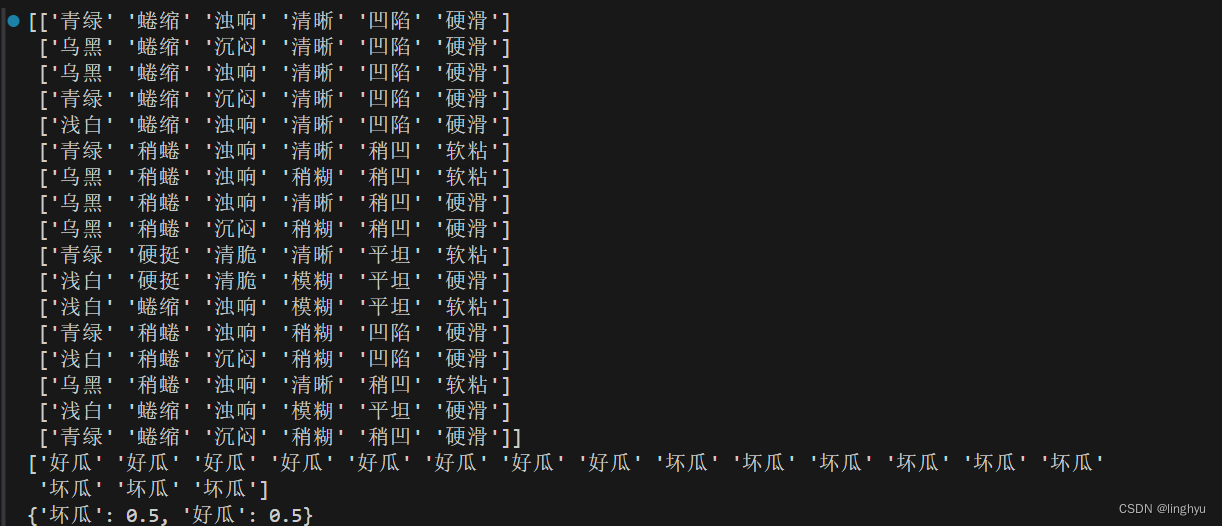
以上查看数据,即标签的分布比例。
from pprint import pprint
import numpy as np
dataset = np.array([# 色泽,根蒂,敲击,纹理,脐部,触感, 好坏['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],['乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '好瓜'],['乌黑', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],['青绿', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '好瓜'],['浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],['青绿', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '好瓜'],['乌黑', '稍蜷', '浊响', '稍糊', '稍凹', '软粘', '好瓜'],['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '硬滑', '好瓜'],['乌黑', '稍蜷', '沉闷', '稍糊', '稍凹', '硬滑', '坏瓜'],['青绿', '硬挺', '清脆', '清晰', '平坦', '软粘', '坏瓜'],['浅白', '硬挺', '清脆', '模糊', '平坦', '硬滑', '坏瓜'],['浅白', '蜷缩', '浊响', '模糊', '平坦', '软粘', '坏瓜'],['青绿', '稍蜷', '浊响', '稍糊', '凹陷', '硬滑', '坏瓜'],['浅白', '稍蜷', '沉闷', '稍糊', '凹陷', '硬滑', '坏瓜'],['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '坏瓜'],['浅白', '蜷缩', '浊响', '模糊', '平坦', '硬滑', '坏瓜'],['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑', '坏瓜']
])features = {'色泽': ['青绿', '乌黑', '浅白'],'根蒂': ['蜷缩', '稍蜷', '硬挺'],'敲击': ['浊响', '沉闷', '清脆'],'纹理': ['清晰', '稍糊', '模糊'],'脐部': ['凹陷', '稍凹', '平坦'],'触感': ['硬滑', '软粘']
}labels = ["好瓜", "坏瓜"]class Bayes:def __init__(self, features: dict, labels: list) -> None:self.features = featuresself.labels = labelsself.feature_classes = list(self.features.keys())self.condi_prob = {}self.prior_prob = {}self._statistic = {}self._samples = 0for i in self.labels:self.prior_prob[i] = 1 / len(self.labels)self.condi_prob[i] = {}self._statistic[i] = 0for j in self.feature_classes:self.condi_prob[i][j] = {}for k in self.features[j]:self.condi_prob[i][j][k] = 1 / len(self.features[j])self._statistic['.'.join([i, j, k])] = 0def bayes_prob(self, arr):plist = []for i in self.labels:idx = 0p = self.prior_prob[i]for j in self.feature_classes:p *= self.condi_prob[i][j][arr[idx]]idx += 1plist.append(p)return plistdef train(self, X, Y):rows, cols = X.shapefor i in range(rows):self._statistic[Y[i]] += 1for j in range(cols):self._statistic['.'.join([Y[i], self.feature_classes[j], X[i, j]])] += 1self._samples += 1for i in self.labels:self.prior_prob[i] = (self._statistic[i] + 1) / (self._samples+len(self.labels))for j in self.feature_classes:for k in self.features[j]:self.condi_prob[i][j][k] = (self._statistic['.'.join([i, j, k])] + 1) / (self._statistic[i] + len(self.features[j]))def predic(self, X):rows, cols = X.shaperes = []for i in range(rows):y = self.bayes_prob(X[i])res.append(y)res = np.argmax(res, axis=1)res = [self.labels[x] for x in res]return np.array(res)def show_params(self) -> str:pprint(self.prior_prob)pprint(self.condi_prob , sort_dicts=False)# pprint(self._statistic)if __name__ == "__main__":X = dataset[:, :6]Y = dataset[:, 6]print(X)print(Y)clf = Bayes(features, labels)clf.show_params()clf.train(X, Y)clf.show_params()Yp = clf.predic(X)print(f"原始:{Y}\n预测:{Yp}\n准确率:{np.sum(Y==Yp)/len(Y)}")
进行初始化,初始化函数来构建一个朴素贝叶斯分类器,接收两个参数:features和labels。
将features和labels分别赋值给实例变量,计算特征类的列表,并初始化self.condi_prob(条件概率)、self.prior_prob(先验概率)、self._statistic(统计信息)和self._samples(样本数量)。
函数遍历labels中的每个标签,并计算先验概率,遍历features中的每个特征,并初始化一个空字典,用于存储特征在标签下的条件概率。
函数遍历features中的每个特征和每个可能的特征值,并计算条件概率。同时,它将特征值与标签组合成一个字符串,并将其作为键添加到字典中,初始值为0。
接下来训练朴素贝叶斯分类器。
第一部分遍历所有样本,统计每个类别和每个特征值出现的次数。使用两个字典`_statistic`和`_samples`来存储这些统计信息。
第二部分计算先验概率和条件概率。先验概率是指在给定类别的情况下,某个特征值出现的概率。条件概率是指在给定某个特征值的情况下,某个类别出现的概率。使用贝叶斯公式来计算这些概率。
然后,准备计算贝叶斯的概率函数。初始化一个空列表,用于存储每个类别的贝叶斯概率。遍历类标签列表,对于每个类标签,计算先验概率。遍历特征类别列表,对于每个特征类别,计算条件概率。将计算出的条件概率乘以先验概率,并将结果添加到返回值列表中。
定义一个分类器, 申请一个空列表,用于存储每个样本的预测结果。调用前面我们提到的计算贝叶斯的概率函数方法计算当前行的概率分布。返回数组中每行的最大值的下标,即预测结果。最后将预测结果转换为对应的类别标签存储为一维数组。
在训练前后我们可以分别显示模型参数。打印两个字典,计算先验概率、条件概率,下图为训练前模型参数:
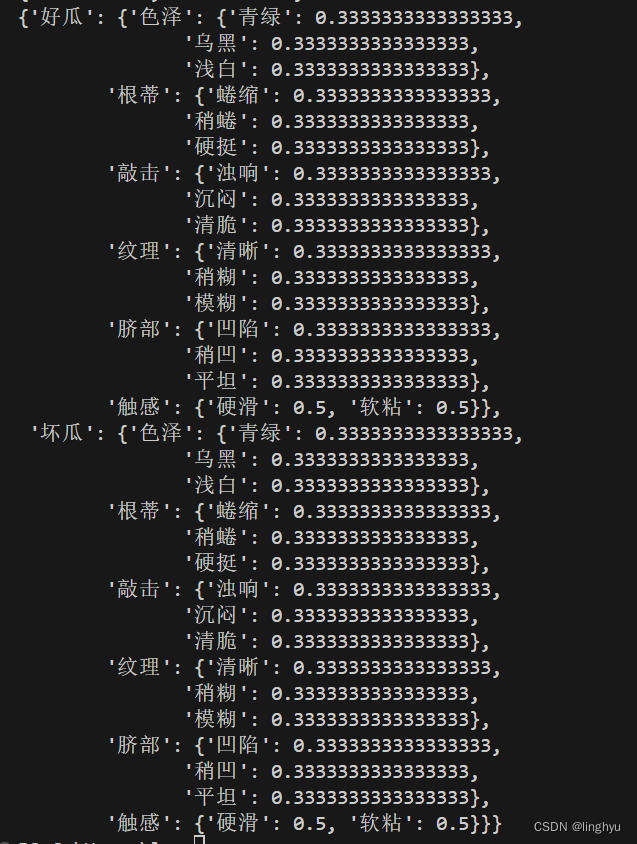
下图为训练后模型参数:
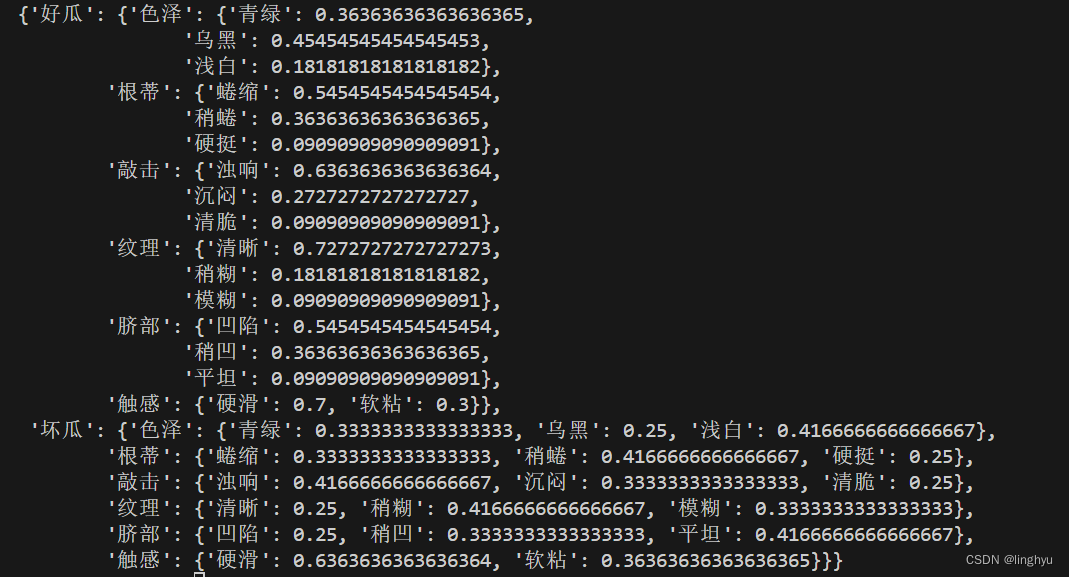
以下是模型的两次预测结果及准确率,趋于一致:


具体来说,原始的标签包括了17个样本,其中有8个属于"好瓜"类别,9个属于"坏瓜"类别。预测的结果与原始标签进行了比较,其中有14个样本的预测结果与原始标签一致,3个样本的预测结果与原始标签不一致。
根据比较结果计算得到的准确率为0.8235,召回率为0.875。这个准确率表明,贝叶斯算法在这个测试数据集上的分类表现较为良好,但仍有改进的空间。