目录
一、查找
1.1查找的基本概念
1.2顺序查找
1.3折半查找（二分查找）
1.4散列表的查找
1.4.1基本概念
1.4.2散列函数的构造方法
1.4.3解决冲突的方法
二、排序
2.1排序的基本概念
2.2插入排序
2.2.1直接插入排序：
2.2.2希尔排序
2.3交换排序
2.3.1冒泡排序
2.3.2快速排序
一、查找
1.1查找的基本概念
①查找：在数据集合中，寻找满足魔偶找条件的数据元素的过程。
②查找表（查找结构）：用于查找的数据集合
③关键字：数据元素中某个数据项的值，用它可以标识一个数据元素；
主关键字：关键字可以唯一地标识一个记录。
④平均查找长度：所有查找过程中进行的关键字的比较次数的平均值
ASL=(Pi·Ci)
1.2顺序查找
基本思想：
从线性表的一端开始，逐个检查关键字是否满足给定的条件。若查找到某个元素的关键字满足条件，则查找成功，返回该元素在线性表中的位置。若查找到表的另一端，仍未找到符合给定条件的元素，则返回查找失败的信息。
算法实现：
typedef struct{ElemType *elem;int TableLen;
}SSTable;int Search_Sep(SSTable ST,ElemType key){ST.elem[0]=key;for(i=ST.TableLen;ST.elem[i]!=key;--i); //从后往前查找return i;
} 注：对线性链表只能进行顺序查找。
1.3折半查找（二分查找）
仅适用于有序的顺序表
算法实现：
int Binary_Search(SeqList L,ElemType key){int low=0,high=L.TableLen-1,mid;while(low<=high){mid=(low+high)/2;if(L.elem[mid]==key)return mid;else if(L.elem[mid]>key)high=mid-1;elselow=mid+1;}
}
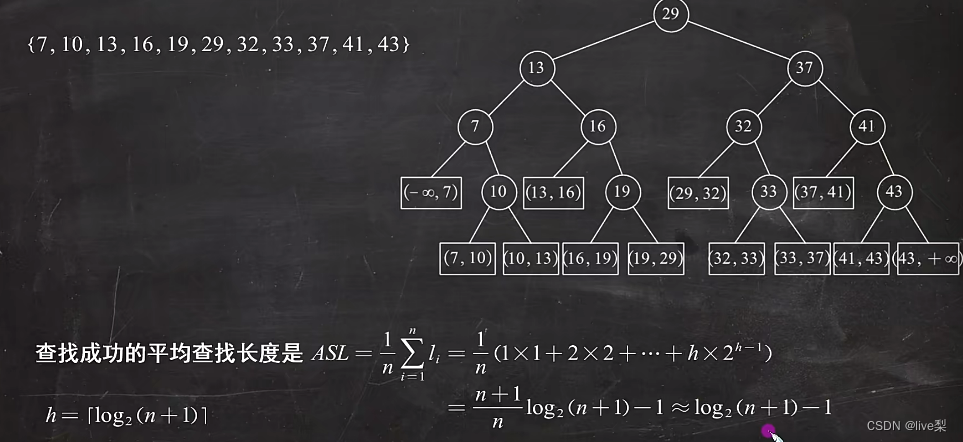时间复杂度为O(n)=log2(n)
1.4散列表的查找
1.4.1基本概念
散列函数：Hash(key)=Addr
同义词：散列函数可能会把两个或两个以上的不同关键字映射到同一地址。
例3%4=3,7%4=3,3和7为同义词
1.4.2散列函数的构造方法
①直接定址法：H(key)=key H(key)=a*key+b
②除留余数法： m，取一个不大于但最接近或等于m的质数p
③数字分析法
④平方取中法
1.4.3解决冲突的方法
①开放定址法：可存放新表项的空闲地址既向它的同义词表项开放，又向它的非同义词表项开放。其数学递推公式为：Hi=(H(key)+di)%m
对di的取法：
a.线性探测法：di=0,1,2,...,m-1
b.平方探测法：di=0*0,1*1,-1*(-1),2*2,-2*(-2),....k*k,-k*(-k) ,k<=m/2
c.再散列法：di=Hash2(key)
例：散列表的构造
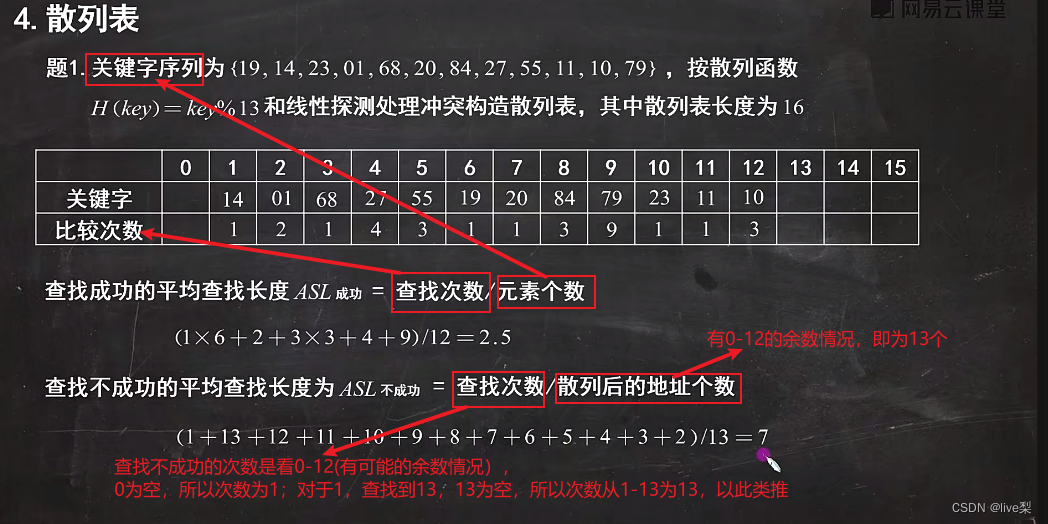
②拉链法：为了避免非同义词发生冲突，把所有的同义词存储在一个线性链表中
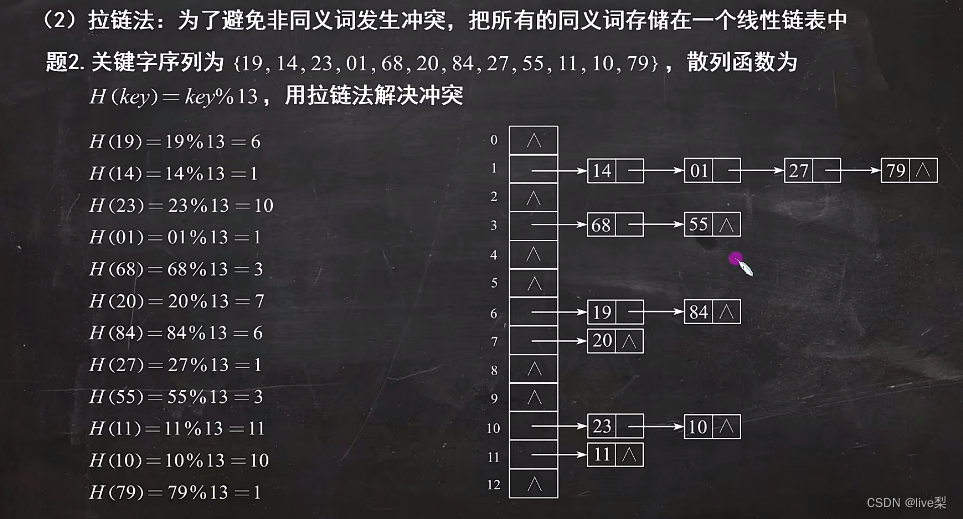
注：散列表的查找长度取决于3个因素：散列函数、处理冲突的方法、装填因子
装填因子=表中记录数n/散列长度m
散列表的平均查找长度依赖于装填因子，不直接依赖于n或m，当
越大时，表示装填的记录越满，发生冲突的可能性就越大。
二、排序
2.1排序的基本概念
①排序：重新排列表中的元素，使表中的元素满足按关键字有序。
②稳定性，在排序前后序列中的Ri始终领先于Rj，则称所用的排序方法时稳定的（考虑相对位置）
③内部排序：指在排序期间元素全部存在内存中的排序
方法：插入排序、交换排序、选择排序、归并排序和基数排序（前四种需要经过比较和移动两种操作）
④外部排序：指在排序期间元素无法全部同时存放在内存中，必须在排序的过程中根据要求不断地在内，外存之间移动的排序。
2.2插入排序
基本思想：每次将一个待排序的记录按其关键字大小插入到前面已排好序的子序列中，直到全部记录插入完成。
2.2.1直接插入排序：
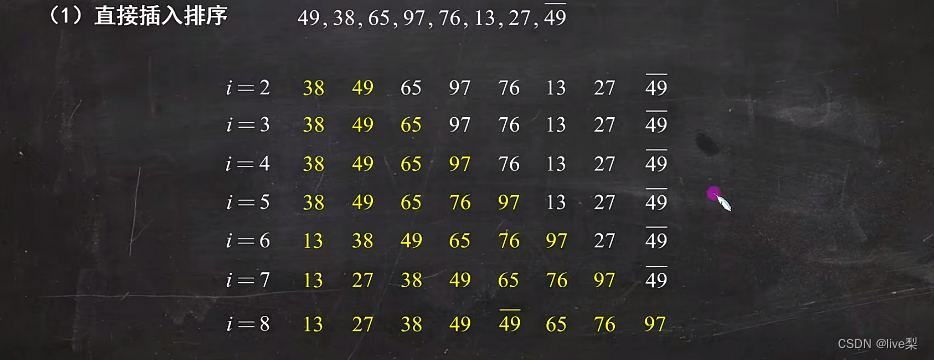
算法实现：
void InsertSort(ElemType A[[],int n){int i,j;for(i=2,i<=n;i++)if(A[i]<A[i-1]){A[0]=A[i];for(j=i-1;A[0]<A[j];--j)A[j+1]=A[j];A[j+1]=A[0];}
}空间复杂度：O(1); 时间复杂度：O(n*n); 稳定性：稳定
2.2.2希尔排序
把像个某个增量的记录组成一个子表，对各个子表分别进行直接插入排序，当整个表中的元素已呈基本有序时，再对全体记录进行依次直接插入排序。
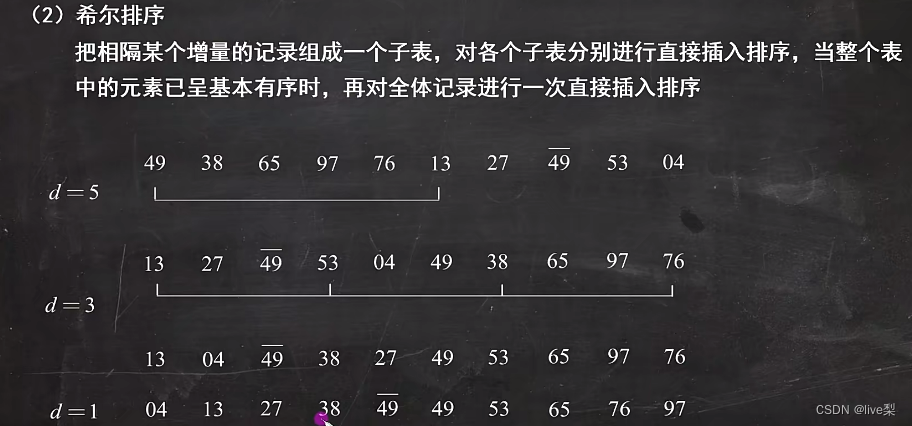
空间复杂度：O(1); 时间复杂度不确定；稳定性：不稳定
例：
2.3交换排序
2.3.1冒泡排序
基本思想：从后往前（或从前往后）两两比较相邻元素的值，若为逆序，则进行交换，直到序列比较完，第一趟冒泡结束，结果是将最小的元素交换到待排序列的第一个位置（或将最大的元素交换到待排序列的最后一个位置）。
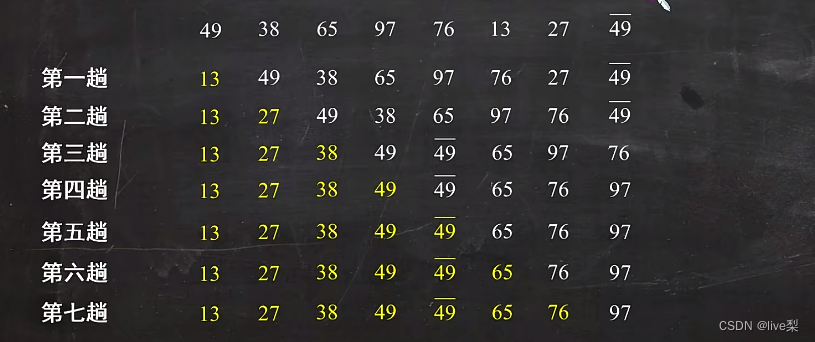
算法实现：
void BubbleSort(ElemType A[], int n){for(i=0;i<n-1;i++)flag=false;for(j=n-1;j>i;j--)if(A[j-1]>A[j]{swap(A[j-1],A[j]);flag=true;}if(flag==false)return;} 空间复杂度：O(1); 时间复杂度：O(n*n) ; 稳定性：稳定
2.3.2快速排序
基本思想：在待排序表L[1....,n]中任取一个元素pivot作为枢轴，（通常取首元素），通过一趟快速排序将待排序表划分为独立的两部分L[1,,,k-1]和L[k+1...n],pivot放在了最终位置L[k]中
空间复杂度：O(log2(n)); 时间复杂度：O(nlog2(n)); 稳定性：不稳定
·快速排序是所有内部排序算法中平均性能最优的排序算法，但它并不适用于原本有序或基本有序的记录序列进行排序。
2.4选择排序
2.4.1简单选择排序
基本思想：假设排序表为L[1....,n],第i趟排序即从L[i...,n]中选择关键字最小的元素与L[i]交换
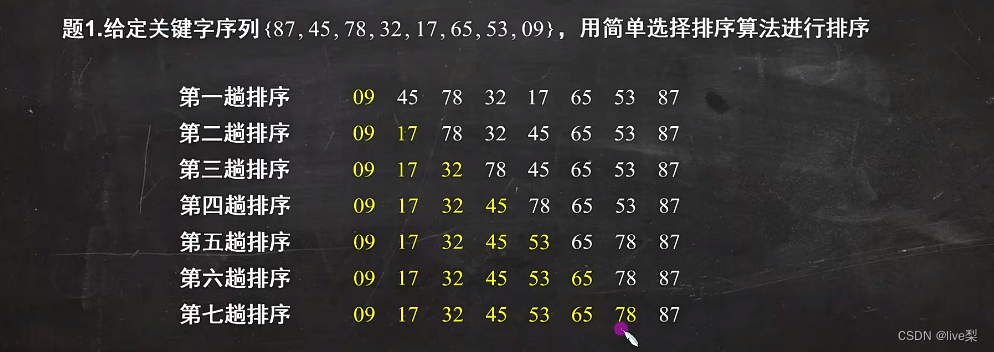
void SelectSort(ElemType A[],int n){for(i=0;i<n-1;i++){min=i;for(j=i+1;j<n;j++)if(A[j]<A[min]min=j;if(min!=i)swap(A[i],A[min]);}
}空间复杂度：O(1); 时间复杂度：O(n*n) ; 稳定性：不稳定
2.4.2堆排序
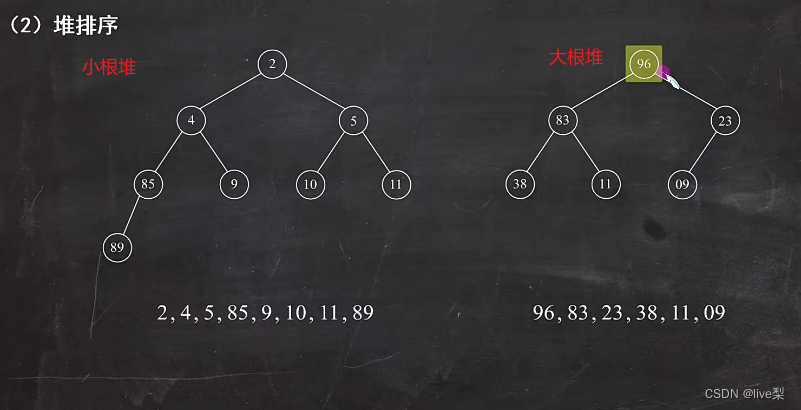
构造大根堆：双亲结点大于孩子结点
堆的删除操作
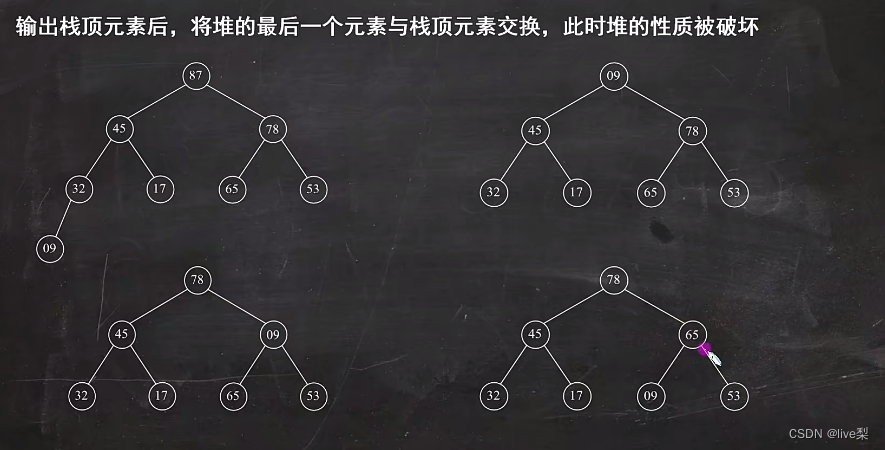
堆的插入操作
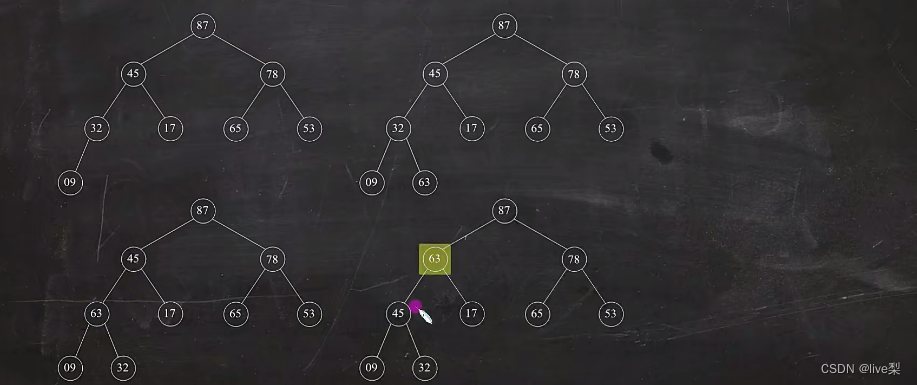
空间复杂度： O(1); 时间复杂度：O(nlog2(n)); 稳定性：不稳定
2.4归并排序
“归并”是将两个或两个以上的有序表组合成一个新的有序表。
2.4.1 2路归并排序
空间复杂度：O(n); 时间复杂度：O(nlog2(n)); 稳定性：稳定
2.5基数排序
基数排序不基于比较和移动进行排序，而基于关键字各位的大小排序。
①对个位进行排序
②对十位进行排序
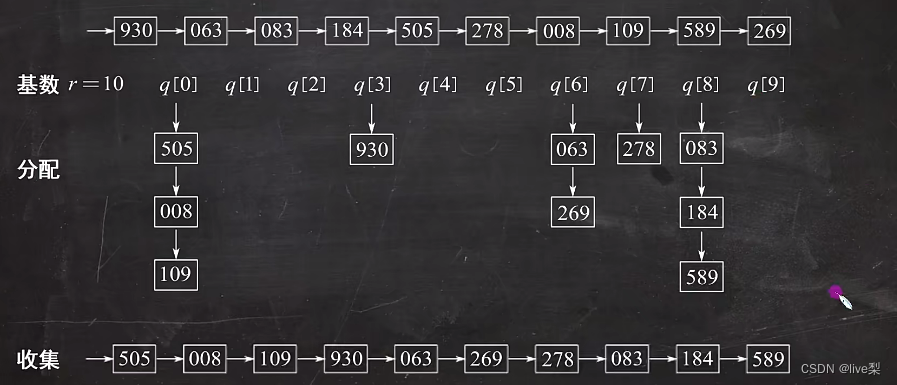
③对百位进行排序
空间复杂度：O(r)；时间复杂度：O(d(n+r)),d表示分配和收集的趟数；稳定性：稳定
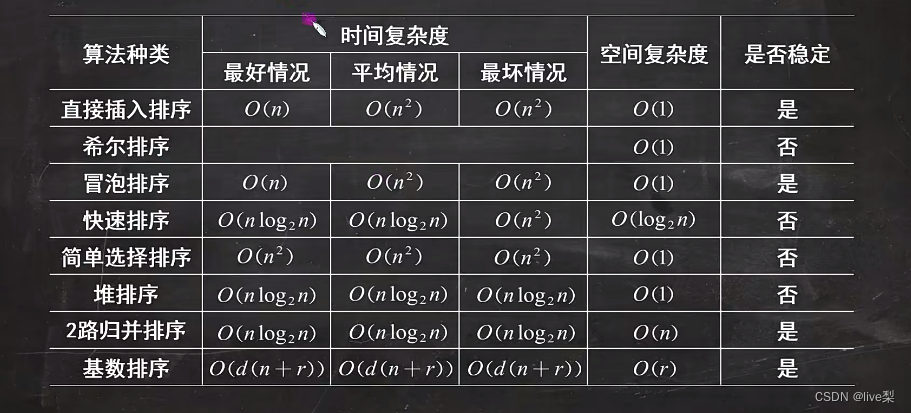
2.6各种排序算法的比较
