星期一:
补cf global round26 C2 cf传送门

思路:有效操作2只有一次,且反转后不会再出现负数,即后面能贡献 2^n-i个方案,再乘上前面 2^(k>=0的次数)
代码如下:
ll n;
ll a[N];
ll qpow(int n){ll res=1,a=2;while(n){if(n&1) res=res*a%mod;a=a*a%mod;n>>=1;}return res;
}
void solve(){cin >> n;for(int i=1;i<=n;i++){cin >> a[i];}ll sum=0,cmp=0;for(int i=1;i<=n;i++){sum+=a[i];cmp=min(sum,cmp);}if(!cmp){cout << qpow(n) << "\n"; return ;}ll k=0,now=1,ans=0;for(int i=1;i<=n;i++){k+=a[i];if(k==cmp) ans+=qpow(n-i+now-1),ans%=mod;now+=k>=0;}cout << ans << "\n";
}星期二:
补西南科技第二十届 牛客传送门

有点怪的题
思路:

代码如下:
ll n;
void solve(){cin >> n;int x,y; cin >> x >> y;set<int>st1,st2;int sa=0;for(int i=1;i<=x;i++){int w,num; cin >> w >> num;st1.insert(w);}for(int i=1;i<=y;i++){int w,num; cin >> w >> num;st2.insert(w);sa+=st1.find(w)!=st1.end();}cout << min(min((ll)st1.size()-sa,n/2)+min((ll)st2.size()-sa,n/2)+1ll*sa,n);
}星期四:
补二十届西南科技 K 差分 牛客传送门

罕见的差分题
思路:主要在于如何处理扩散,向两边都扩散,那么可以正着跑一遍处理向右扩散,反着处理向左
对于所有操作,做个前缀差分和后缀差分,cnt 记录当前有多少个在扩散的点,w记录点的权值
代码如下:
const int N=2e6+10;
ll n;
int pre[N],pos[N],w[N];
ll a[N];
void solve(){int m; cin >> n >> m;while(m--){int a,b,c; cin >> a >> b >> c;if(a==1){w[b]+=c;pre[b]++,pre[b+c]--;pos[b]++,pos[max(0,b-c)]--;}else{w[b]-=c;pre[b]--,pre[b+c]++;pos[b]--,pos[max(0,b-c)]++;}}ll sum=0,cnt=0;for(int i=1;i<=n;i++){sum+=w[i]-cnt;cnt+=pre[i];a[i]=sum;}sum=0,cnt=0;for(int i=n;i;i--){sum+=w[i]-cnt;cnt+=pos[i];a[i]+=sum-w[i];}for(int i=1;i<=n;i++) cout << a[i] << " ";
}顺手做的区间dp vj传送门
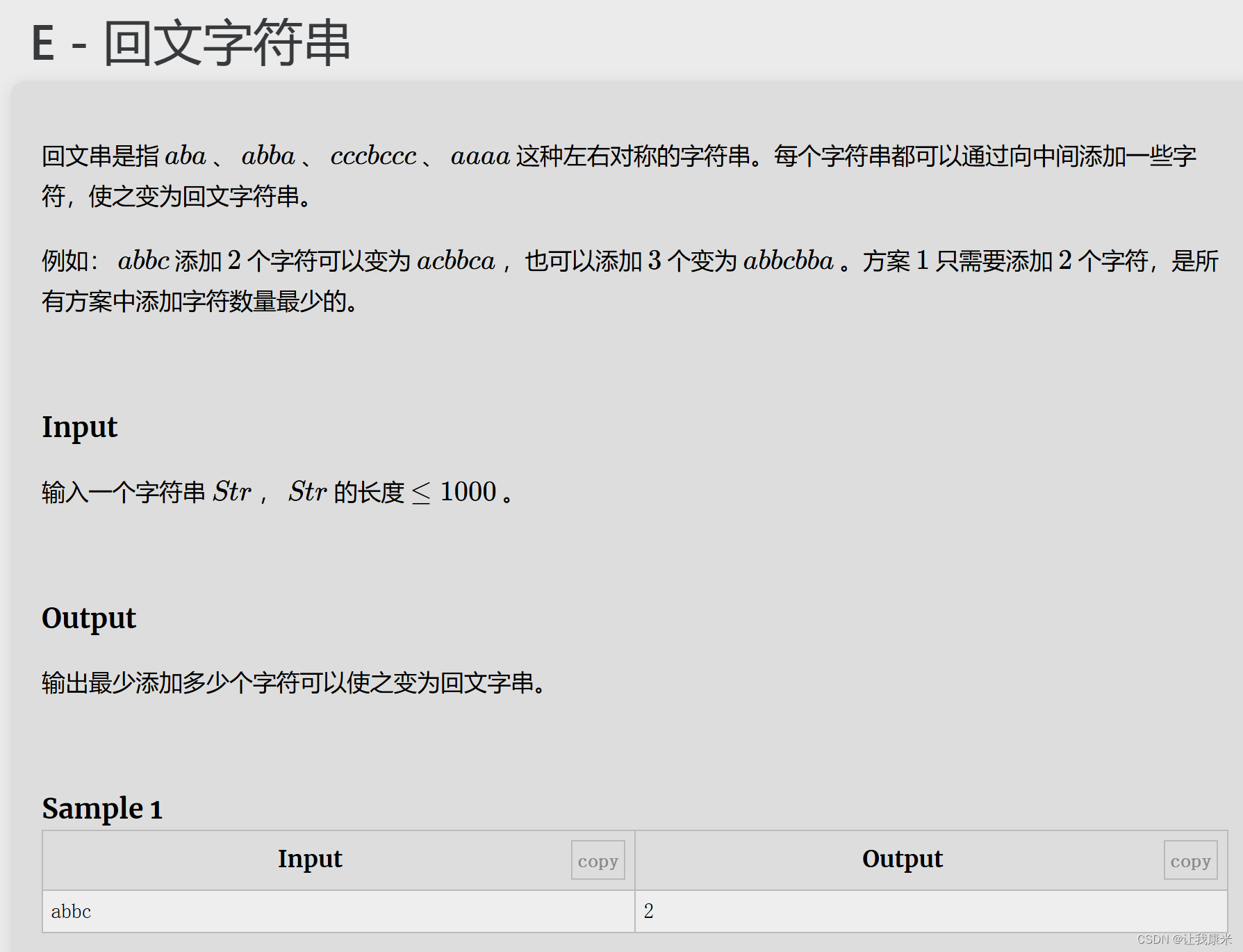
代码如下:
ll n;
ll dp[1010][1010];
void solve(){string s; cin >> s;n=s.size(); s=" "+s;memset(dp,0x3f,sizeof dp);for(int i=1;i<=n;i++){dp[i][i]=0;if(i<n && s[i]==s[i+1]) dp[i][i+1]=0;}for(int len=1;len<n;len++){for(int l=1;l+len-1<=n;l++){int r=l+len-1;if(l<r-1 && s[l]==s[r]) dp[l][r]=min(dp[l+1][r-1],dp[l][r]);if(l>1){if(s[l-1]==s[r]) dp[l-1][r]=min({dp[l][r-1],dp[l][r]+1,dp[l-1][r]});else dp[l-1][r]=min(dp[l][r]+1,dp[l-1][r]);}if(r<n){if(s[l]==s[r+1]) dp[l][r+1]=min({dp[l+1][r],dp[l][r]+1,dp[l][r+1]});else dp[l][r+1]=min(dp[l][r]+1,dp[l][r+1]);}}}cout << dp[1][n];
}星期五:
dp求方案数 vj传送门
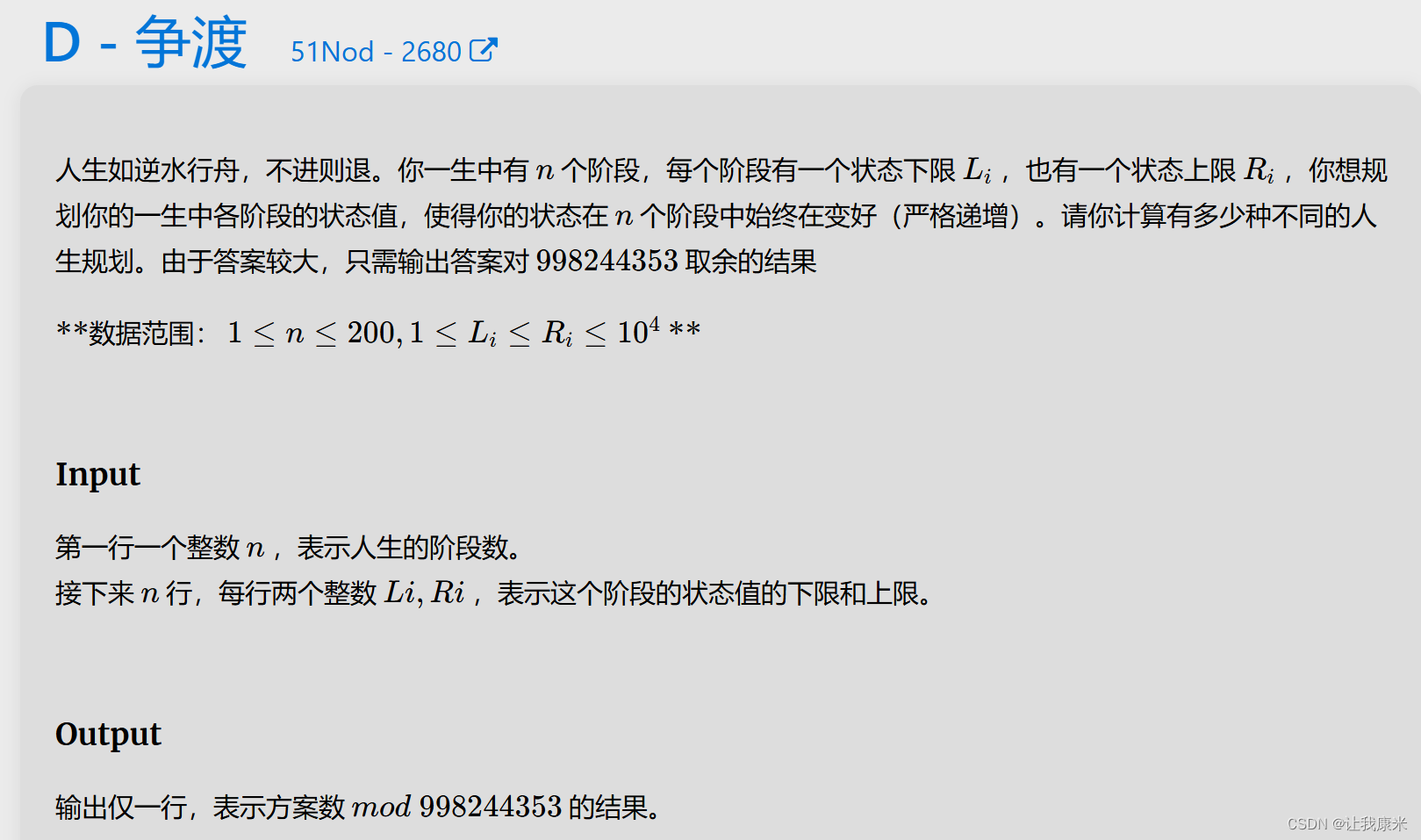
思路:dp【i】【j】表示第 i个阶段,状态值为 j的方案数
,用前缀和优化一下就行,注意不要漏掉 i-1的方案数
代码如下:
const int mod=998244353;
ll n;
ll l[220],r[220];
ll dp[220][10004];
void solve(){cin >> n;for(int i=1;i<=n;i++){cin >> l[i] >> r[i];}for(int i=l[1];i<=r[1];i++) dp[1][i]=1;int bt=l[1];for(int i=2;i<=n;i++){bt=max(l[i],1ll*bt+1);for(int j=l[i-1];j<bt;j++) dp[i-1][j]+=dp[i-1][j-1],dp[i-1][j]%=mod;//前缀和for(int j=bt;j<=r[i];j++){dp[i][j]+=dp[i-1][j-1],dp[i][j]%=mod;dp[i-1][j]+=dp[i-1][j-1],dp[i-1][j]%=mod;//前缀和}}ll ans=0;for(int i=bt;i<=r[n];i++) ans+=dp[n][i],ans%=mod;cout << ans << "\n";
}很典的完全背包方案数 vj传送门
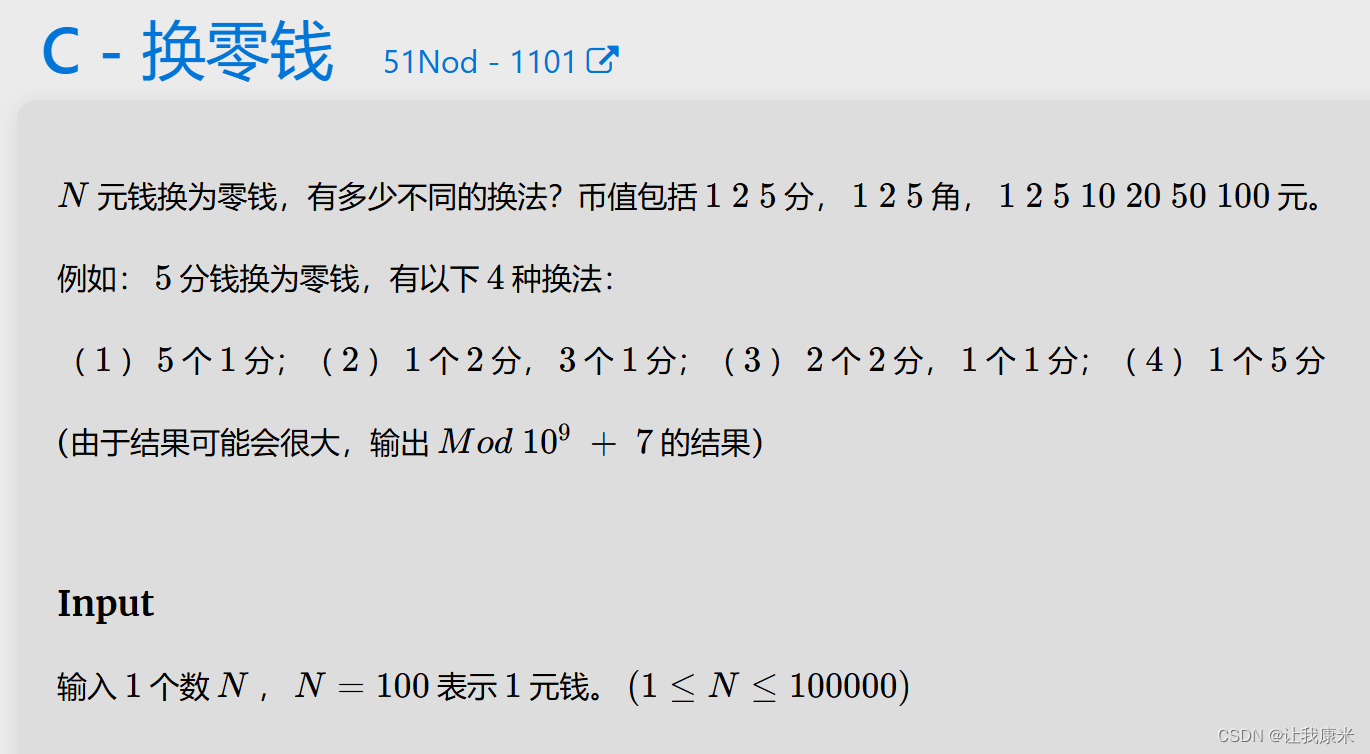
虽然很典,但还是调了一会儿,主要在一些细节上不太熟悉
代码如下:
const int N=1e5+10;
const int mod=1e9+7;
ll n;
ll dp[N];
int a[]={0,1,2,5,10,20,50,100,200,500,1000,2000,5000,10000};
void solve(){cin >> n;for(int i=0;i<=n;i++) dp[i]=1;for(int i=2;i<=13;i++){for(int j=a[i];j<=n;j++)dp[j]+=dp[j-a[i]],dp[j]%=mod;}cout << dp[n];
}上楼梯3 vj传送门
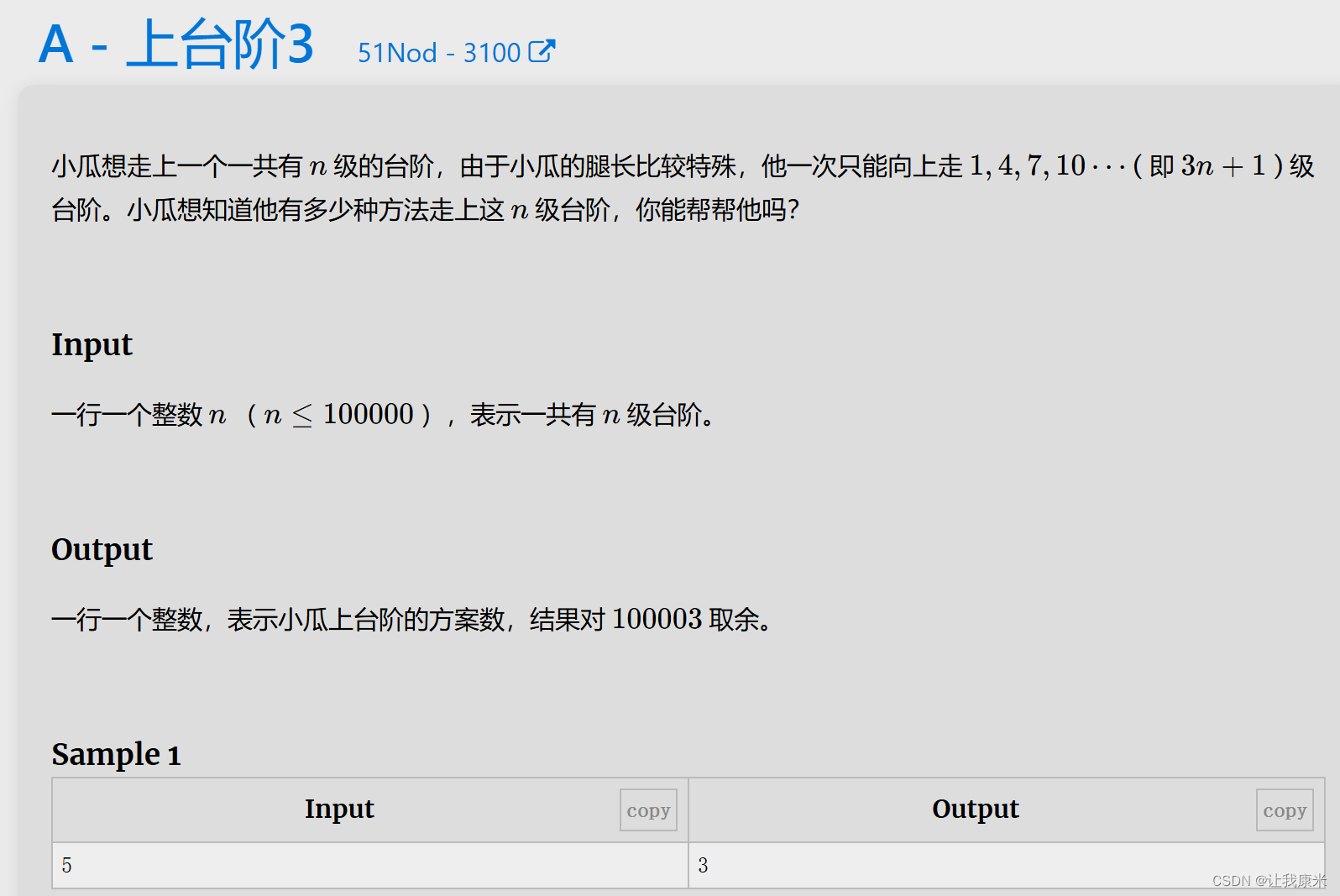
需要推式子的转移
思路:
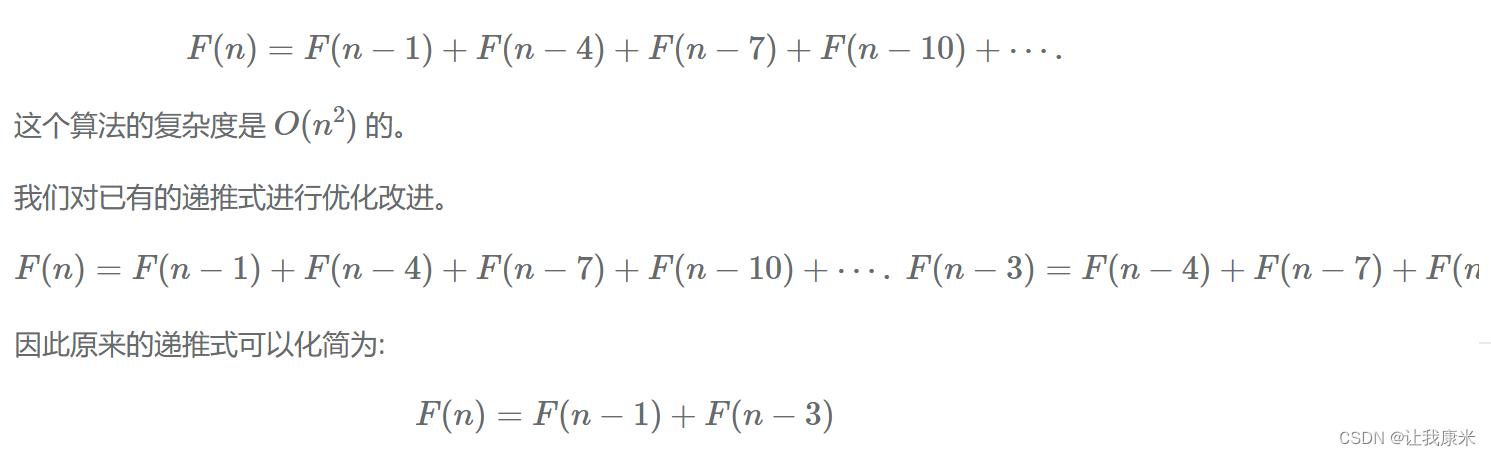
代码如下:
const int N=1e5+10;
ll n;
const int p=100003;
ll dp[N];
void solve(){cin >> n;dp[1]=1;dp[2]=1;for(int i=3;i<=n;i++)dp[i]=(dp[i-1]+dp[i-3])%p;cout << dp[n];
}线性dp vj传送门

思路:dp【i】【0/1】表示考虑到第 i个,第 i个选 1或b【i】的最大值
代码如下:
const int N=2e6+10;
ll n;
int b[N];
ll dp[N][2];
void solve(){cin >> n;for(int i=1;i<=n;i++) cin >> b[i];for(int i=2;i<=n;i++){dp[i][0]=max(dp[i-1][0],dp[i-1][1]+b[i-1]-1);dp[i][1]=max(dp[i-1][0]+b[i]-1,dp[i-1][1]+abs(b[i]-b[i-1]));}cout << max(dp[n][0],dp[n][1]);
}