内容摘要
主要介绍我对本书的一些自我感觉比较亮点地方的总结。
第一章
算法
- 算法有两条线索,数据结构、算法策略。





算法特性

时间复杂度

常见算法时间复杂度
时间复杂度的渐进上界

渐进精确界
用渐进上界和渐进下界逼近,
空间复杂度

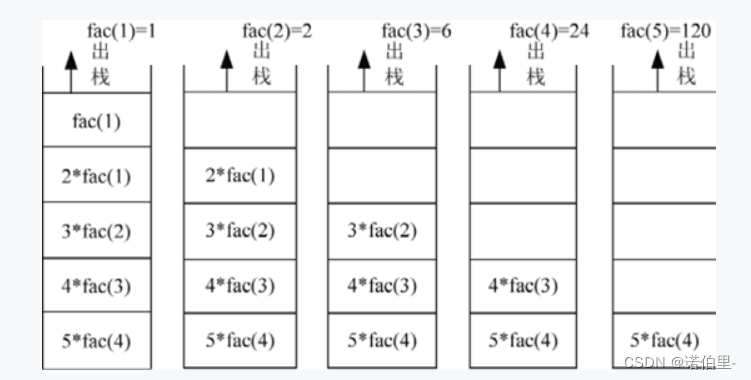
递归
- 递归包括递推和回归。
- 递推是将原问题不断分解成子问题,直到达到结束条件,返回最近子问题的解;然后逆向逐一回归,最终到达递推开始的原问题,返回原问题的解。
栈
后进先出。
数学知识
斐波那契数列

斐波那契数列和黄金分割比的关系:

第二章
贪心算法

贪心算法特性
贪心选择性质
- 原问题的整体最优解可以通过一系列局部最优解的选择得到。
- 原问题变为一个相似的但规模更小的子问题,而后的每一步都是当前最佳的选择。
- 选择依赖于已做出的选择,但不依赖于未作出的选择。
- 程序的运行过程中无回溯过程。
最优子结构性质
一个问题的最优解包含其子问题的最优解。
贪心算法案例
冒泡排序采用了贪心算法。
背包问题

创建栈

正态分布
大部分数据呈现正态分布,因此遍历是不合理的。
最小生成树
- 权值最小的生成图。
- 离散数学无向连通图相关知识。
避圈法
Kruskal算法和Prim算法

第三章
快速排序(sort)
快排原理
向左走、向右走,直到重合,重复此过程。
快排特点
- 分解难,合并易。
- 先难后易。
- 原地排序。
排序复杂度

合并排序(归并排序)
合并排序特点
- 分解容易,合并难。
- 先易后难。
- 需要辅助空间(辅助数组),异地排序。
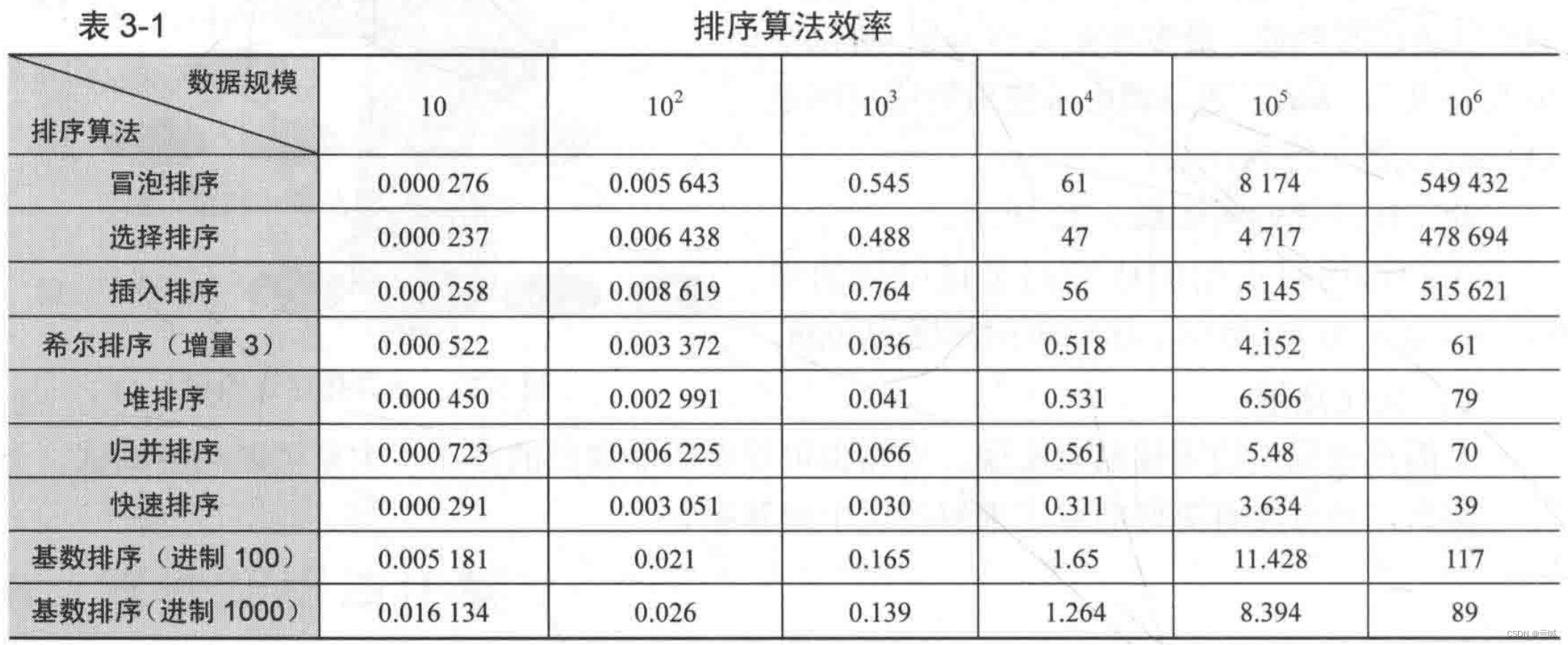
排序算法效率
大整数乘法
- 分治。
- 乘法运算采用倒序保存结果。
时间复杂度

空间复杂度

四次乘法变三次乘法

时间复杂度变化

注意事项

第四章
动态规划
最优子结构

子问题重叠

如何使用动态规划


编辑距离

构造最优解

二叉搜索树

最优二叉搜索树

最优二叉树的最优值递归式(动态规划的查表法)

搜索成本(平均比较次数)

- 关键字结点的搜索成本

- 每个实结点的搜索成本=结点的深度*搜索概率。
- 虚结点的搜索成本

- 每个虚结点的搜索成本=结点的深度*搜索概率。
搜索概率

第五章
回溯法
隐约束(剪枝函数)
约束函数和限界函数
时间复杂度
n皇后
- 以行为主导


最优加工顺序

贝尔曼规则

第六章
贪心策略对购物车问题的缺陷

队列
此类问题可以用队列(先近先出)解决
回溯法与分支限界法

第七章
线性规划
处理线性规划问题

单纯形表
特殊位置

单纯形算法
将目标函数由非基本变量表示
最大网络流

可行流
- 容量约束
- 流量守恒
残余网络

附录F
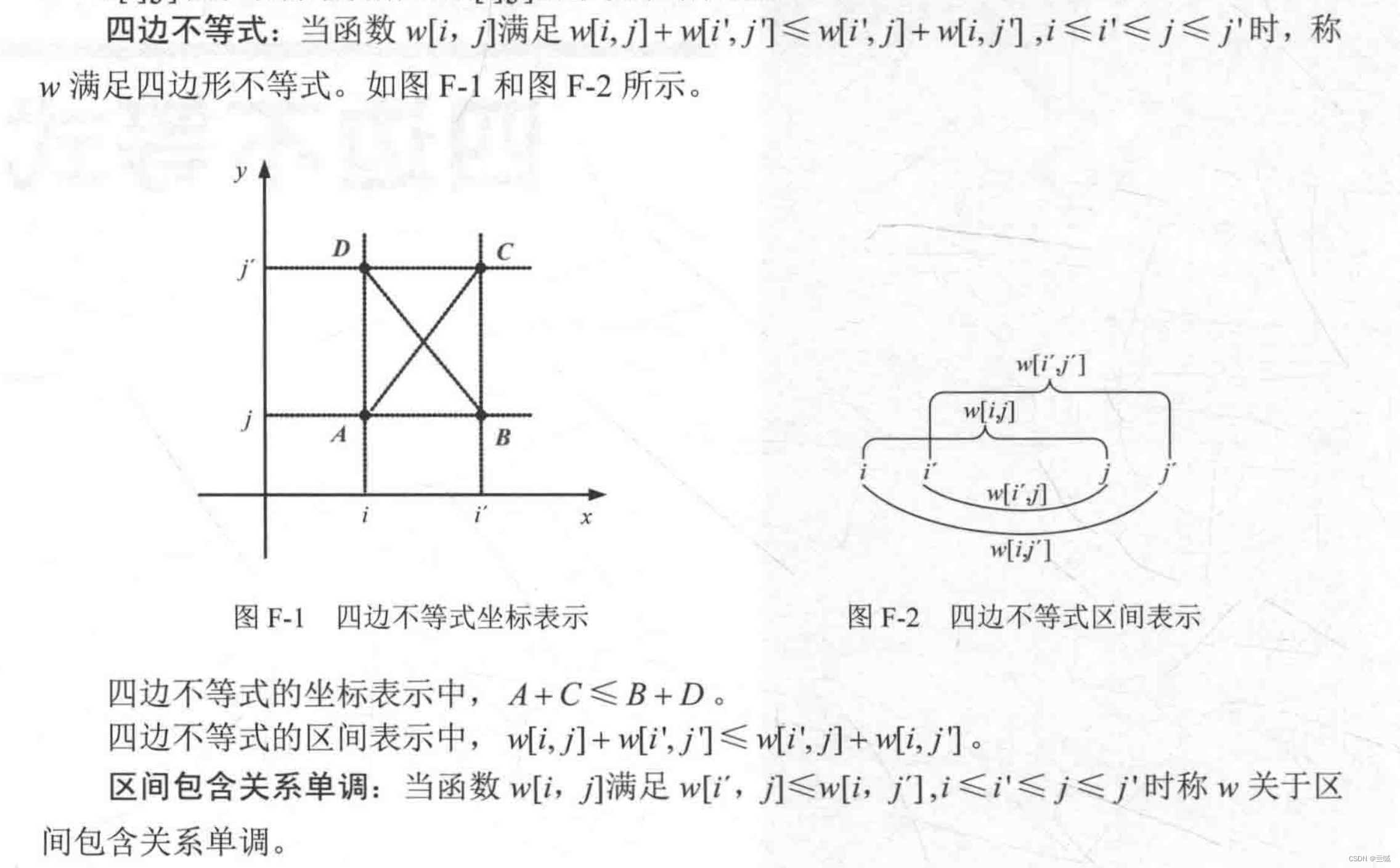
四边不等式
本书免费访问路径
-
https://gateway.pinata.cloud/ipfs/bafykbzaceauicbfg6xaw22pjmb7p75u4qrwiu77c4kgqwwy2gpwcvnr3v3ea4?filename=%E8%B6%A3%E5%AD%A6%E7%AE%97%E6%B3%95.pdf
-
https://www.cnblogs.com/aerer/p/9931040.html