递归回溯法经典——组合（python）

关于递归，虽然每次看代码都能明白别人代码的大体意思，但实际上当自己动手写的时候，往往没有头绪。

为了解决这个问题，我感觉我们需要深入探究模拟别人代码的全过程，了解递归回溯的基本像树一样的全过程，才能帮助我们更好的理解，当然写这篇文章也是给自己一个记录复习，可能无法实质性的帮助到大家哈哈哈哈

原题链接为：77. 组合 - 力扣（LeetCode）

把组合问题抽象为如下树形结构

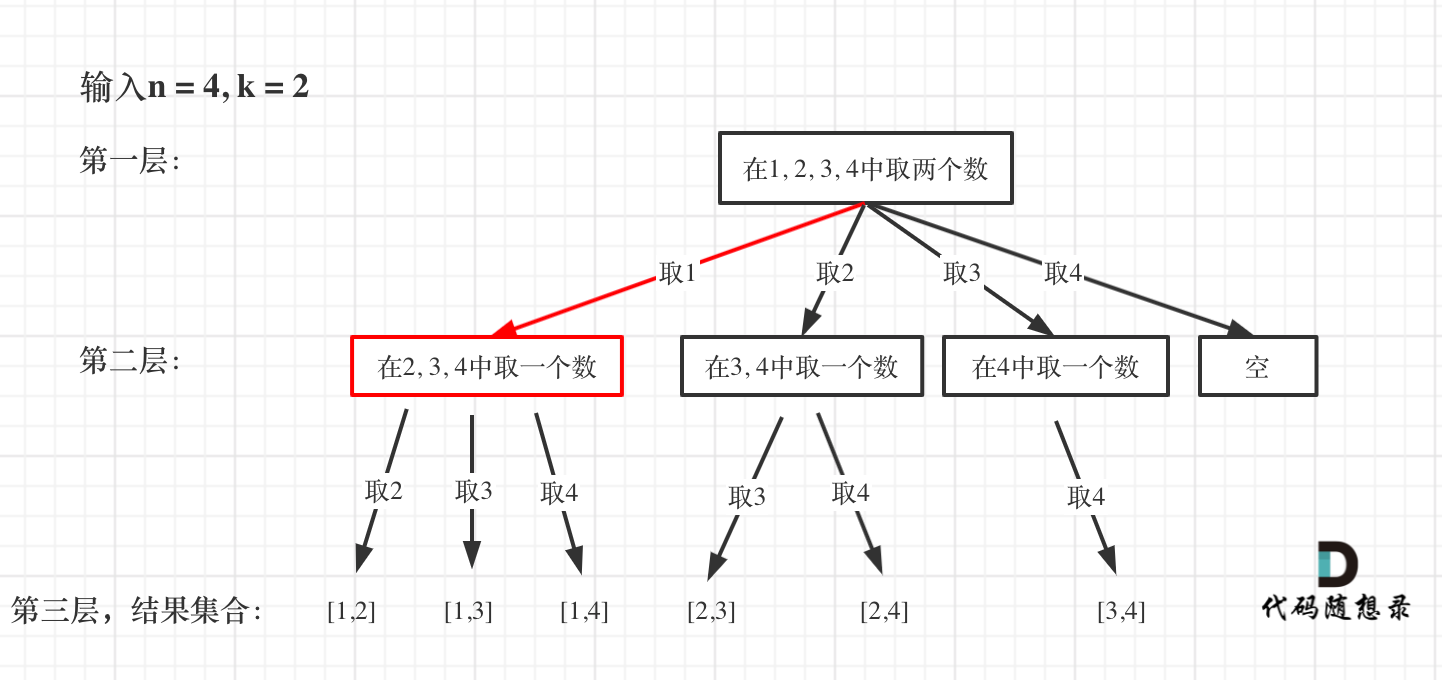
然后下面的回溯三部曲大家应该也明白，我再赘述一下：

递归函数的返回值以及参数
回溯函数终止条件
单层搜索的过程

这里我直接贴出卡尔老师的代码，因为代码的浅理解也比较容易

class Solution:def combine(self, n: int, k: int) -> List[List[int]]:res = []path = []def backtrack(n, k, StartIndex):if len(path) == k:res.append(path[:])returnfor i in range(StartIndex, n + 1):path.append(i)backtrack(n, k, i+1)path.pop()backtrack(n, k, 1)return res

下面也就是本博客主要的出发点：模拟程序运行的过程——

建议大家结合着画着二叉树来模拟

当n=4和k=2时，程序的完整具体运行过程如下：

初始化res为空列表，初始化path为空列表。
调用backtrack函数，传递参数n=4，k=2，StartIndex=1。
判断如果当前path列表中的元素数量等于k，将其复制一份并添加到res列表中，并立即返回。
进入for循环，循环变量i从StartIndex(1开始)到n+1(5)，依次取值为1, 2, 3, 4.
在每个for循环迭代中，将变量i添加到path列表中。
调用backtrack函数，传递参数n=4，k=2，StartIndex=i+1(i的初始值为1，则第一次调用将传递2作为StartIndex参数)。
重复步骤3到步骤6，直到path列表中的元素数量等于k。
当path列表中的元素数量等于k时，将其复制一份并添加到res列表中，并立即返回上一级backtrack函数的调用。
回溯，将最后一个添加到path列表中的元素弹出。
回到步骤5，继续循环。重复步骤5到步骤9，直到所有迭代结束。
返回res列表作为输出结果。

接下来是更具体的过程（以下为chatgpt所写，可能略有出入，但大体的思路见解可以供我们参考，当我们理解里面的总体过程，我们也就对回溯法有了进一步的认识）

当 n=4, k=2 时，程序的运行过程如下：

首先初始化结果列表 res 和路径列表 path。

res = [] path = []
调用 backtrack 函数，并传入参数 n=4, k=2, StartIndex=1。

执行 backtrack(n=4, k=2, StartIndex=1)。
判断当前路径长度是否等于 k，如果是则将当前路径添加到结果列表中并返回。
对于循环中的每个 i，执行以下操作：

a. 将 i 添加到路径列表 path 中。

b. 递归调用 backtrack 函数，传入参数 n、k、i+1。
- 当 i=1 时，执行 backtrack(n=4, k=2, StartIndex=2)。
  - 判断当前路径长度是否等于 k，长度为 1 不等于 k，继续执行。
  - 对于循环中的每个 j，在路径中加入 j 并递归调用 backtrack 函数，传入参数 n、k、j+1。由于此时 k=2，因此只需要找到两个数即可，所以 j 的取值范围为 [2, 4]。
    - 当 j=2 时，执行 backtrack(n=4, k=2, StartIndex=3)。
      - 判断当前路径长度是否等于 k，长度为 2 等于 k，将路径 [1,2] 添加到结果列表中。
    - 当 j=3 时，执行 backtrack(n=4, k=2, StartIndex=4)。
      - 判断当前路径长度是否等于 k，长度为 2 等于 k，将路径 [1,3] 添加到结果列表中。
    - 当 j=4 时，由于此时已经没有元素可以添加到路径中，直接返回。
- 当 i=2 时，执行 backtrack(n=4, k=2, StartIndex=3)。
  - 判断当前路径长度是否等于 k，长度为 1 不等于 k，继续执行。
  - 对于循环中的每个 j，在路径中加入 j 并递归调用 backtrack 函数，传入参数 n、k、j+1。由于此时 k=2，因此只需要找到两个数即可，所以 j 的取值范围为 [3, 4]。
    - 当 j=3 时，执行 backtrack(n=4, k=2, StartIndex=4)。
      - 判断当前路径长度是否等于 k，长度为 2 等于 k，将路径 [2,3] 添加到结果列表中。
    - 当 j=4 时，由于此时已经没有元素可以添加到路径中，直接返回。
- 当 i=3 时，执行 backtrack(n=4, k=2, StartIndex=4)。
  - 判断当前路径长度是否等于 k，长度为 1 不等于 k，继续执行。
  - 对于循环中的每个 j，在路径中加入 j 并递归调用 backtrack 函数，传入参数 n、k、j+1。由于此时 k=2，因此只需要找到两个数即可，所以 j 的取值范围为 [4]。
    - 当 j=4 时，由于此时已经没有元素可以添加到路径中，直接返回。
- 当 i=4 时，由于此时已经没有元素可以添加到路径中，直接返回。
backtrack 函数执行完毕后，将结果列表 res 返回。

所以最终的输出结果为 [[1, 2], [1, 3], [2, 3], [1, 4], [2, 4], [3, 4]]。

参考大佬的这篇文章：代码随想录 (programmercarl.com)https://www.programmercarl.com/0077.%E7%BB%84%E5%90%88.html#%E5%85%B6%E4%BB%96%E8%AF%AD%E8%A8%80%E7%89%88%E6%9C%AC