给定 n 给非负整数，表示每个宽度为 1 的柱子的高度图，计算按照此排列的柱子，下雨之后能能接到多少雨水。

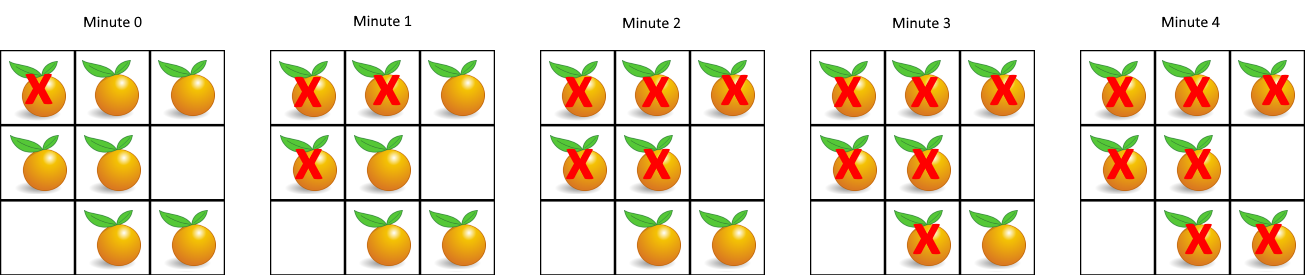
输入：height = [0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1]

输出：6

解释：上面是由数组 [0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1] 表示的高度图，在这种情况袭，可以接住 6 个单位雨水（蓝色部分表示雨水）。

就是用一个数组表示一个条形图，问这个条形图最多能接多少水。

1 暴力解法

具体来讲，对于位置 i 能装下多少水呢？

能装下 2 格。为什么呢？因为位置 i 处能达到的水柱的高度和其左边的最高柱子、右边的最高柱子有关。其左边最高柱子的高度是 2，其右边最高柱子的高度是 3，因为 height[i] 的高度是 0，所以位置 i 处能装下 2 格的水。

这里我们假设左右两个最高柱子的高度分别为 leftMax 和 rightMax，位置 i 处的水柱高度就是 min(leftMax, rightMax) - height[i]。

根据以上的思路：

fun trap(height: Array<Int>): Int {val n = height.sizevar res = 0// 位置 0 和位置 n - 1 处无法存储水for (i in 1 until n - 1) {var leftMax = 0 // 位置 i 处左边最高的柱子var rightMax = 0 // 位置 i 处右边最高的柱子// 寻找左边最高的柱子，这里到 i 是因为后面要 -height[i]for (j in 0..i) {leftMax = leftMax.coerceAtLeast(height[j])}// 寻找右边最高的柱子，这里从 i 开始是因为后面要 -height[i]for (j in i until n) {rightMax = rightMax.coerceAtLeast(height[j])}res += leftMax.coerceAtMost(rightMax) - height[i]}return res
}

2 备忘录优化

在暴力算法中，需要计算每个位置的 leftMax 和 rightMax，我们可以直接先把结果计算出来，不需要每次都遍历。

定义两个数组 leftMax 和 rightMax 充当备忘录，leftMax[i] 表示位置 i 左边最高的柱子高度，rightMax[i] 表示位置 i 右边最高的柱子高度。预先把这两个数组准备好，避免重复计算：

fun trap(height: Array<Int>): Int {val n = height.sizevar res = 0// 数组备忘录val leftMax = IntArray(n)val rightMax = IntArray(n)// 初始化leftMax[0] = height[0]rightMax[n - 1] = height[n - 1]for (i in 1 until n) {leftMax[i] = height[i].coerceAtLeast(leftMax[i - 1])}for (i in n - 2 downTo 0) {rightMax[i] = height[i].coerceAtLeast(rightMax[i + 1])}for (i in 1 until n - 1) {res += leftMax[i].coerceAtMost(rightMax[i]) - height[i]}return res
}

备忘录算法和暴力算法的思路差不多，就是避免了重复计算。

4 双指针解法

fun trap(height: Array<Int>): Int {val n = height.sizevar res = 0var left = 0var right = n - 1// 左边最高柱子的高度和右边最高柱子的高度var leftMax = height[0]var rightMax = height[n - 1]while (left < right) {leftMax = leftMax.coerceAtLeast(height[left])rightMax = rightMax.coerceAtLeast(height[right])if (leftMax < rightMax) { // 左边的柱子低于右边柱子的高度，水的高度只和较低的柱子有关res += leftMax - height[left]left++} else { // 右边的柱子低于左边柱子的高度，水的高度只和较低的柱子有关res += rightMax - height[right]right--}}return res
}