数据结构历年考研真题对应知识点（树的基本概念）

5.1树的基本概念

5.1.2基本术语

【森林中树的数量、边数和结点数的关系（2016）】

5.1.3树的性质

【树中结点数和度数的关系的应用（2010、2016）】

【指定结点数的三叉树的最小高度分析（2022）】

5.1树的基本概念

5.1.2基本术语

下面结合图5.1中的树来说明一些基本术语和概念。

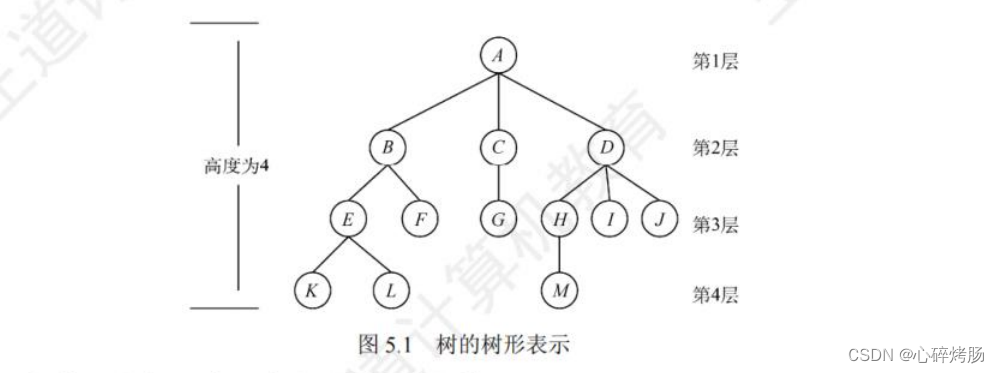
1）祖先、子孙、双亲、孩子、兄弟和堂兄弟。
祖先：考虑结点K，从根A到结点K的唯一路径上的所有其他结点，称为结点K的祖先。

子孙：如结点B是结点K的祖先，而K是B的子孙，结点B的子孙包括EFK.L。

双亲：路径上最接近结点K的结点E称为K的双亲，而K为E的孩子。根A是树中唯一没有双亲的结点。

兄弟：有相同双亲的结点称为兄弟，如结点K和结点L有相同的双亲E，即K和L为兄弟。

堂兄弟：双亲在同一层的结点互为堂兄弟，结点G与E，E，H，I，J互为堂兄弟。

2）结点的度和树的度。
树中一个结点的孩子个数称为该结点的度，树中结点的最大度数称为树的度。如结点B的度为 2，结点D的度为3，树的度为3。

3）分支结点和叶结点。
度大于0的结点称为分支结点(又称非终端结点)；度为0(没有孩子结点)的结点称为叶结点(又称终端结点)。在分支结点中，每个结点的分支数就是该结点的度。

4)结点的深度、高度和层次。
结点的层次：从树根开始定义，根结点为第1层，它的孩子为第2层，以此类推。

结点的深度：就是结点所在的层次。

树的高度(或深度)：是树中结点的最大层数。图5.1中树的高度为4。

结点的高度：是以该结点为根的子树的高度。

5）有序树和无序树。
树中结点的各子树从左到右是有次序的，不能互换，称该树为有序树，否则称为无序树。

假设图 5.1为有序树，若将子结点位置互换，则变成一棵不同的树。

6）路径和路径长度。
树中两个结点之间的路径是由这两个结点之间所经过的结点序列构成的，而路径长度是路径上所经过的边的个数。

注意：因为树中的分支是有向的，即从双亲指向孩子，所以树中的路径是从上向下的，同一双亲的两个孩子之间不存在路径。

7）森林

【森林中树的数量、边数和结点数的关系（2016）】

森林是 m(m≥0)棵互不相交的树的集合。森林的概念与树的概念十分相近，因为只要把树的根结点删去就成了森林。反之，只要给m棵独立的树加上一个结点，并把这 m棵树作为该结点的子树，则森林就变成了树。

注意：上述概念无须刻意记忆，根据实例理解即可。考研时不大可能直接考查概念，而都是结合具体的题目考查。做题时，遇到不熟悉的概念可以翻书，练习得多自然就记住了。

5.1.3树的性质

树具有如下最基本的性质:

【树中结点数和度数的关系的应用（2010、2016）】

1）树的结点数n等于所有结点的度数之和加1。
结点的度是指该结点的孩子数量，每个结点与其每个孩子都由唯一的边相连，因此树中所有结点的度数之和等于树中的边数之和。

树中的结点(除根外)都有唯一的双亲，因此结点数 n等于边数之和加1，即所有结点的度数之和加1。

2）度为m的树中第i层上至多有 $m^{i-1}$ 个结点(i => 1)。
第1层至多有1个结点(即根结点)，第2层至多有m个结点，第3层至多有㎡个结点，以此类推。使用数学归纳法可推出第i层至多有 $m^{i-1}$ 个结点。

3）高度为h的 m 叉树至多有 $(m^{h}-1) / (m-1)$ 个结点。
当各层结点数达到最大时，树中至多有 $1+m+m^{2}+...+m^{h-1}=(m^{h}-1)/(m-1)$ 个结点。

【指定结点数的三叉树的最小高度分析（2022）】

4）度为 m、具有n个结点的树的最小高度h为 $log_{m}(n(m-1)+1)$
为使树的高度最小，在前 h-1 层中，每层的结点数都要达到最大，前 h-1 层最多有 $(m^{h-1}-1) / (m-1)$ 个结点,前h层最多有 $(m^{h}-1) / (m-1)$ 个结点。因此 $(m^{h-1}-1) / (m-1)<n\leqslant (m^{h}-1) / (m-1)$ ，即 $h-1<log_{m}(n(m-1)+1)\leqslant h$ ,