1、matlab卷积运算简介
在Matlab中,卷积运算是一种常见的信号处理和图像处理操作,用于将两个函数或信号进行混合以创建一个新的函数或信号。在Matlab中,卷积运算可以通过使用函数conv来实现。
-
一维卷积:在一维情况下,卷积运算将输入的两个向量进行混合运算,生成一个新的输出向量。在Matlab中,可以使用
conv函数来执行一维卷积,语法为:conv(A, B),其中A和B是进行卷积运算的两个向量。 -
二维卷积:对于二维情况,卷积运算可以在两个二维矩阵之间进行。Matlab中的
conv2函数可以用于执行二维卷积运算,语法为:conv2(A, B),其中A和B是进行二维卷积运算的两个矩阵。 -
N维卷积:对于更高维度的情况,Matlab也提供了
convn函数来执行N维卷积运算。convn函数可以处理多维数组之间的卷积运算,语法为:convn(A, B),其中A和B是进行N维卷积运算的输入数组。
通过利用Matlab中的这些卷积函数,可以方便地进行信号处理、图像处理和其他领域中的卷积运算操作。
2、conv() 卷积和多项式乘法
conv()函数简介
在MATLAB中,conv()函数既可以用于执行卷积运算,也可以用于多项式的乘法。
-
卷积运算:在信号处理中,卷积运算用于两个信号的混合。
conv(x, h)用于计算输入信号x和系统响应h之间的线性卷积。结果存储在一个新的向量中,其长度为length(x)+length(h)-1。这在处理信号滤波、系统建模和数字信号处理中非常有用。 -
多项式乘法:在多项式计算中,
conv()函数还可以用于多项式的乘法操作。当传入两个多项式的系数向量时,conv()函数将返回它们相乘的结果的系数向量。这在处理多项式乘法问题时非常方便。
总之,conv()函数在MATLAB中具有广泛的用途,既可以用于卷积运算,也可以用于多项式的乘法,便于信号处理、系统建模、多项式计算等各种应用领域。
语法
语法1:w = conv(u,v) 返回向量 u 和 v 的卷积。
语法2:w = conv(u,v,shape) 返回如 shape 指定的卷积的分段。
参数
u,v — 输入向量 shape — 卷积的分段 'full' (默认) | 'same' | 'valid'
'full':全卷积 ‘same’:与u大小相同的卷积的中心部分'valid':计算没有补零边缘的卷积部分
3、通过卷积计算多项式乘法
代码及运算
u = [1 0 1 1];
v = [2 7 1];
w = conv(u,v)w =2 7 3 9 8 14、 向量卷积
代码及运算
u = [1 1 1 1];
v = [1 1 1 1 0 0 0 1 1];
w = conv(u,v)w =列 1 至 111 2 3 4 3 2 1 1 2 2 2列 1215、 卷积的中心部分
'same'代码及运算
u = [-1 2 1 3 1 -2 0 1 2];
v = [2 4 -1 1 1];
w = conv(u,v,'same')w =11 7 14 0 -5 8 7 5 -1'full'代码及运算
u = [-1 2 1 3 1 -2 0 1 2];
v = [2 4 -1 1 1];
w = conv(u,v,'full')w =列 1 至 11-2 0 11 7 14 0 -5 8 7 5 -1列 12 至 133 2'valid'代码及运算
u = [-1 2 1 3 1 -2 0 1 2];
v = [2 4 -1 1 1];
w = conv(u,v,'valid')w =14 0 -5 8 76、 conv2() 二维卷积
conv2() 函数简介
在MATLAB中,conv2()函数用于进行二维卷积运算。二维卷积是信号处理和图像处理中常见的操作,用于对图像、矩阵或二维信号进行滤波、特征提取等操作。
conv2()函数的语法为 C = conv2(A, B),其中A是输入的二维矩阵(如图像),B是卷积核(也称为卷积模板)。
具体来说,conv2()函数将卷积核B应用于输入矩阵A,计算在不同位置的元素相乘和求和的结果,并存储在输出矩阵C中。输出矩阵C的大小取决于输入矩阵A和卷积核B的大小。
二维卷积在图像处理中经常用于各种滤波操作,例如模糊、锐化、边缘检测等。通过调整卷积核的值,可以实现不同的滤波效果。conv2()函数的灵活性和简便性使其成为MATLAB中进行二维卷积运算的重要工具。
对于处理图像、模式识别、特征提取等应用来说,熟练掌握conv2()函数能够帮助用户实现各种二维卷积操作,提升数据处理和分析的效率。
语法
语法1:C = conv2(A,B) 返回矩阵 A 和 B 的二维卷积。
语法2:C = conv2(u,v,A) 首先求 A 的各列与向量 u 的卷积,然后求每行结果与向量 v 的卷积。
语法3:C = conv2(___,shape) 根据 shape 返回卷积的子区。
1)二维卷积
代码及运算
A = rand(3);
B = rand(4);
Cfull = conv2(A,B)%6*6
Csame = conv2(A,B,'same')%中心部位Cfull =0.0781 0.8435 1.6181 1.6544 1.5357 0.72130.2367 1.2223 2.9144 3.6484 2.8119 1.09200.5183 1.4313 3.4028 4.2039 3.0881 1.37230.2844 2.0170 2.9532 3.0694 2.6967 0.98390.4857 1.3186 1.8013 1.5967 1.3232 0.48200.5008 0.1639 0.8645 0.2304 0.3948 0.0831Csame =3.4028 4.2039 3.08812.9532 3.0694 2.69671.8013 1.5967 1.32322)例子:提取二维台座边
代码及运算
A = zeros(10);
A(3:7,3:7) = ones(5);
mesh(A)视图效果

1) 计算水平边
代码及运算
u = [1 0 -1]';
v = [1 2 1];
Ch = conv2(u,v,A);
mesh(Ch)视图效果

2)计算垂直边
代码及运算
Cv = conv2(v,u,A);
mesh(Cv)视图效果
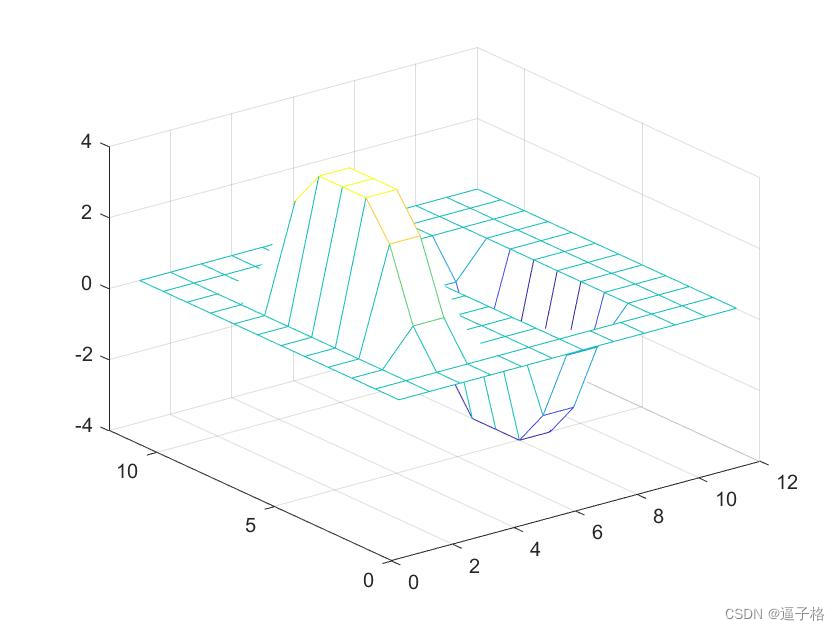
3) 绘制组合边长
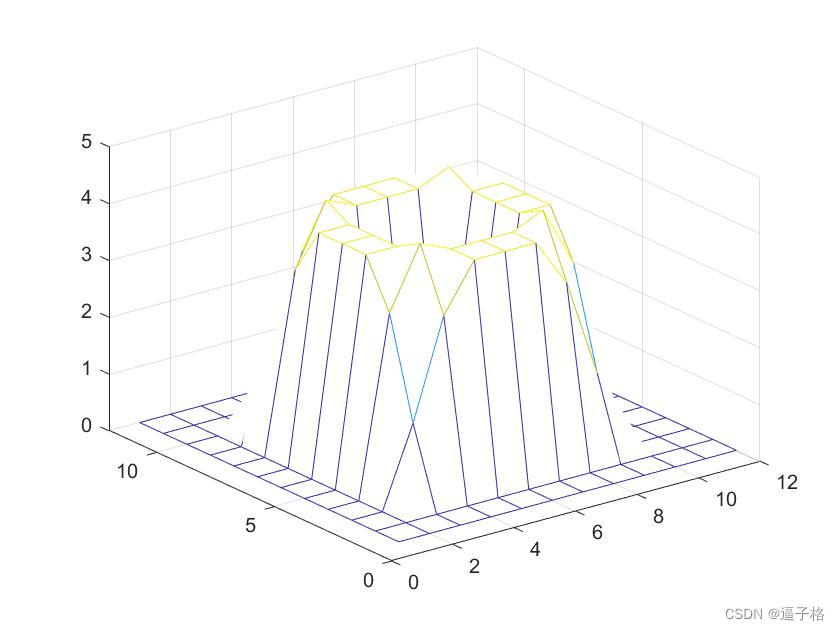
7、convn() N 维卷积
convn()函数简介
在MATLAB中,convn()函数用于进行N维卷积运算,可以处理高维度的数据,而不仅限于二维。N维卷积在图像处理、信号处理和其他科学计算领域中具有广泛的应用。
convn()函数的语法为 C = convn(A, B),其中A是输入的N维数组(可以是多维图像、多维信号等),B是卷积核(也称为卷积模板)。
具体来说,convn()函数将卷积核B应用于输入数组A的每个维度,计算在不同位置的元素相乘和求和的结果,并存储在输出数组C中。输出数组C的大小和输入数组A的大小有关,取决于卷积核B的大小和维度。
N维卷积可以用于各种高维数据的处理,例如多维图像滤波、信号处理中的卷积运算、神经网络中的卷积层操作等。通过使用convn()函数,用户可以方便地对多维数据进行卷积操作,实现特定的数据处理和分析任务。
掌握convn()函数可以让用户更灵活地处理各种N维数据,实现更复杂的数据计算和分析操作。在科学研究、工程领域和图像处理等应用中,N维卷积是一个有用的工具,convn()函数为用户提供了方便的实现方式。
语法
语法1:C = convn(A,B) 返回数组 A 和 B 的 N 维卷积。
语法2:C = convn(A,B,shape) 根据 shape 返回卷积的子区。
1)三维卷积
代码及运算
A = rand(2,3,2);
B = 0.25*ones(2,2,2);
C = convn(A,B)C(:,:,1) =0.1765 0.2457 0.0935 0.02430.1845 0.2652 0.3109 0.23010.0080 0.0195 0.2174 0.2059C(:,:,2) =0.3502 0.6570 0.4408 0.13400.4375 0.7644 0.7622 0.43520.0872 0.1074 0.3214 0.3013C(:,:,3) =0.1737 0.4113 0.3472 0.10970.2530 0.4991 0.4512 0.20510.0793 0.0879 0.1040 0.0954代码及运算
A = rand(2,3,2);
B = 0.25*ones(2,2,2);
C = convn(A,B,'same')C(:,:,1) =1.1643 0.8855 0.47740.6798 0.4946 0.2022C(:,:,2) =0.6049 0.4434 0.20440.3586 0.2106 0.0407代码及运算
A = rand(2,3,2);
B = 0.25*ones(2,2,2);
C = convn(A,B,'full')C(:,:,1) =0.0297 0.2697 0.3863 0.14630.1543 0.4794 0.5273 0.20230.1246 0.2097 0.1410 0.0560C(:,:,2) =0.2176 0.5840 0.7355 0.36900.4059 1.0322 1.2911 0.66480.1884 0.4482 0.5556 0.2958C(:,:,3) =0.1878 0.3143 0.3492 0.22270.2516 0.5528 0.7638 0.46250.0638 0.2385 0.4146 0.2398代码及运算
A = rand(2,3,2);
B = 0.25*ones(2,2,2);
C = convn(A,B,'valid')C =0.8574 0.80728、总结
在MATLAB中,卷积运算是一种常见的信号处理和图像处理操作。以下是对卷积运算、二维卷积和N维卷积的总结:
-
卷积运算:
- 在MATLAB中,可以使用
conv()函数进行一维数组或向量的卷积运算。 - 卷积运算可以用于信号处理、系统建模、滤波器设计等领域。
conv()函数返回两个向量的卷积结果的系数向量,可用于多项式乘法等问题。
- 在MATLAB中,可以使用
-
二维卷积:
- 二维卷积是在图像处理中常见的操作,用于对图像进行滤波、特征提取等。
- 在MATLAB中,可以使用
conv2()函数进行二维卷积运算。 conv2()函数将卷积核应用于输入矩阵,计算在不同位置的元素相乘和求和的结果,输出到新的矩阵中。
-
N维卷积:
- N维卷积可以处理高维度的数据,例如多维图像、多维信号等。
- 在MATLAB中,可以使用
convn()函数进行N维卷积运算。 convn()函数可以处理N维数组,将卷积核应用于每个维度,计算元素相乘和求和的结果,输出到新的N维数组中。
总的来说,卷积运算在MATLAB中有着广泛的应用,涉及到信号处理、图像处理、神经网络等各个领域。掌握不同维度的卷积函数,能够帮助用户实现各种数据处理和分析任务,提升工作效率。