回溯算法-以单位人事管理系统为例

1.回溯算法介绍

1.来源

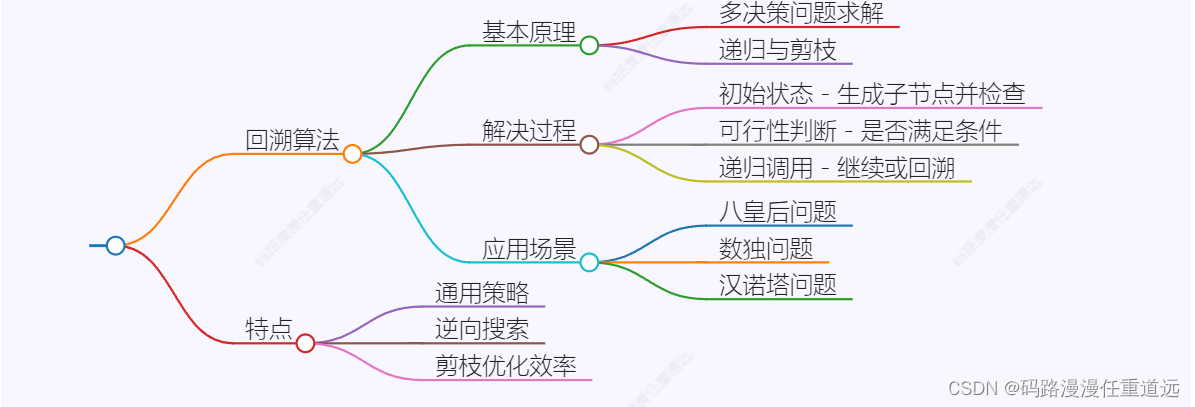
回溯算法也叫试探法，它是一种系统地搜索问题的解的方法。

用回溯算法解决问题的一般步骤：

1、针对所给问题，定义问题的解空间，它至少包含问题的一个（最优）解。

2 、确定易于搜索的解空间结构,使得能用回溯法方便地搜索整个解空间。

3 、以深度优先的方式搜索解空间，并且在搜索过程中用剪枝函数避免无效搜索。

确定了解空间的组织结构后，回溯法就从开始结点（根结点）出发，以深度优先的方式搜索整个解空间。这个开始结点就成为一个活结点，同时也成为当前的扩展结点。在当前的扩展结点处，搜索向纵深方向移至一个新结点。这个新结点就成为一个新的活结点，并成为当前扩展结点。如果在当前的扩展结点处不能再向纵深方向移动，则当前扩展结点就成为死结点。此时，应往回移动（回溯）至最近的一个活结点处，并使这个活结点成为当前的扩展结点。回溯法即以这种工作方式递归地在解空间中搜索，直至找到所要求的解或解空间中已没有活结点时为止。 [2]

2.基本思想

回溯算法的基本思想是：从一条路往前走，能进则进，不能进则退回来，换一条路再试。八皇后问题就是回溯算法的典型，第一步按照顺序放一个皇后，然后第二步符合要求放第2个皇后，如果没有位置符合要求，那么就要改变第一个皇后的位置，重新放第2个皇后的位置，直到找到符合条件的位置就可以了。回溯在迷宫搜索中使用很常见，就是这条路走不通，然后返回前一个路口，继续下一条路。回溯算法说白了就是穷举法。不过回溯算法使用剪枝函数，剪去一些不可能到达最终状态（即答案状态）的节点，从而减少状态空间树节点的生成。回溯法是一个既带有系统性又带有跳跃性的的搜索算法。它在包含问题的所有解的解空间树中，按照深度优先的策略，从根结点出发搜索解空间树。算法搜索至解空间树的任一结点时，总是先判断该结点是否肯定不包含问题的解。如果肯定不包含，则跳过对以该结点为根的子树的系统搜索，逐层向其祖先结点回溯。否则，进入该子树，继续按深度优先的策略进行搜索。回溯法在用来求问题的所有解时，要回溯到根，且根结点的所有子树都已被搜索遍才结束。而回溯法在用来求问题的任一解时，只要搜索到问题的一个解就可以结束。这种以深度优先的方式系统地搜索问题的解的算法称为回溯法，它适用于解一些组合数较大的问题。

2.代码介绍

// 定义一个静态变量用于调试，记录生成的排班组合数量public static int a1 = 0;// 用于生成员工排班的静态方法private static void generateEmployeeSchedules(EmployeeService employeeService) {// 创建一个Scanner对象用于读取用户输入Scanner scanner = new Scanner(System.in);// 读取用户输入的一周天数，并消耗掉输入后的换行符System.out.print("输入一周的天数：");int days = scanner.nextInt();scanner.nextLine(); // 读取用户输入的每天班次数，并消耗掉输入后的换行符System.out.print("输入每天的班次数：");int shiftsPerDay = scanner.nextInt();scanner.nextLine(); // 读取用户输入的每个员工一周内的最大班次数，并消耗掉输入后的换行符System.out.print("输入每个员工在一周内的最大班次数：");int maxShiftsPerEmployee = scanner.nextInt();scanner.nextLine(); // 从EmployeeService获取所有员工信息List<Employee> employees = employeeService.listAllEmployees();// 如果没有员工信息，则打印提示信息并返回if (employees.isEmpty()) {System.out.println("没有职工信息！");return;}// 初始化存储所有排班组合的列表List<List<Integer>> allSchedules = new ArrayList<>();// 初始化一个二维布尔数组，用于记录员工是否已经被安排在特定的天和班次boolean[][] used = new boolean[employees.size()][days];// 初始化一个整型数组，用于记录每个员工已经被安排的班次数int[] employeeShiftCounts = new int[employees.size()];// 调用递归方法开始生成排班计划generateSchedules(0, days, shiftsPerDay, new ArrayList<>(), allSchedules, used, employeeShiftCounts, maxShiftsPerEmployee);// 打印排班组合的数量限制提示信息System.out.println("所有可能的排班组合（最多显示20个）：");// 初始化一个计数器，用于限制打印的排班组合数量int count = 0;// 遍历所有生成的排班组合并打印for (List<Integer> schedule : allSchedules) {a1++; // 调试：增加排班组合计数器// 如果打印的排班组合数量达到限制，则打印提示信息并退出循环if (count++ >= 20) {System.out.println("... 更多的排班组合未显示。");break;}// 打印当前排班组合的详细信息printSchedule(schedule, employees, days, shiftsPerDay);}// 打印总共生成的排班组合数量，用于调试System.out.println("总共生成的排班组合数量：" + allSchedules.size());}// 递归方法，用于生成排班计划private static void generateSchedules(int currentShiftIndex, // 当前正在考虑的班次索引int days, // 一周的天数int shiftsPerDay, // 每天的班次数List<Integer> currentSchedule, // 当前正在构建的排班计划List<List<Integer>> allSchedules, // 存储所有可能的排班组合的列表boolean[][] used, // 记录员工是否已经被安排的二维布尔数组int[] employeeShiftCounts, // 记录每个员工已经被安排的班次数的数组int maxShiftsPerEmployee // 每个员工一周内的最大班次数) {// 如果已经考虑完所有的班次，则将当前的排班计划添加到所有排班组合中if (currentShiftIndex == days * shiftsPerDay) {allSchedules.add(new ArrayList<>(currentSchedule));return;}// 计算当前班次所在的天数int currentDay = currentShiftIndex / shiftsPerDay;// 遍历所有员工，尝试为每个员工安排班次for (int employeeIndex = 0; employeeIndex < used.length; employeeIndex++) {// 如果员工在当前天没有被安排过，并且没有达到最大班次数，则为该员工安排班次if (!used[employeeIndex][currentDay] && employeeShiftCounts[employeeIndex] < maxShiftsPerEmployee) {// 将员工添加到当前排班计划中currentSchedule.add(employeeIndex);// 标记员工在当前天已被安排used[employeeIndex][currentDay] = true;// 增加员工的班次数employeeShiftCounts[employeeIndex]++;// 递归调用，为下一个班次安排员工generateSchedules(currentShiftIndex + 1, days, shiftsPerDay, currentSchedule, allSchedules, used, employeeShiftCounts, maxShiftsPerEmployee);// 回溯：减少员工的班次数，取消员工在当前天的安排employeeShiftCounts[employeeIndex]--;used[employeeIndex][currentDay] = false;// 从当前排班计划中移除员工currentSchedule.remove(currentSchedule.size() - 1);}}}// 打印排班计划的方法private static void printSchedule(List<Integer> schedule, List<Employee> employees, int days, int shiftsPerDay) {// 打印排班组合编号，用于调试System.out.println("排班组合：" + a1);// 遍历每一天for (int day = 0; day < days; day++) {// 打印当前天的标题System.out.println("第 " + (day + 1) + " 天：");// 遍历当天的每个班次for (int shift = 0; shift < shiftsPerDay; shift++) {// 根据排班计划中的索引获取员工编号int employeeIndex = schedule.get(day * shiftsPerDay + shift);// 根据员工编号获取员工对象Employee employee = employees.get(employeeIndex);// 打印员工的班次信息System.out.println("  第 " + (shift + 1) + " 班次：" + employee.getName());}}// 打印空行，用于分隔不同的排班组合System.out.println();}