第29天,贪心part03,快过半了(ง •_•)ง💪,编程语言:C++
目录
134.加油站
135. 分发糖果
860.柠檬水找零
406.根据身高重建队列
134.加油站
文档讲解:代码随想录加油站
视频讲解:手撕加油站
题目:
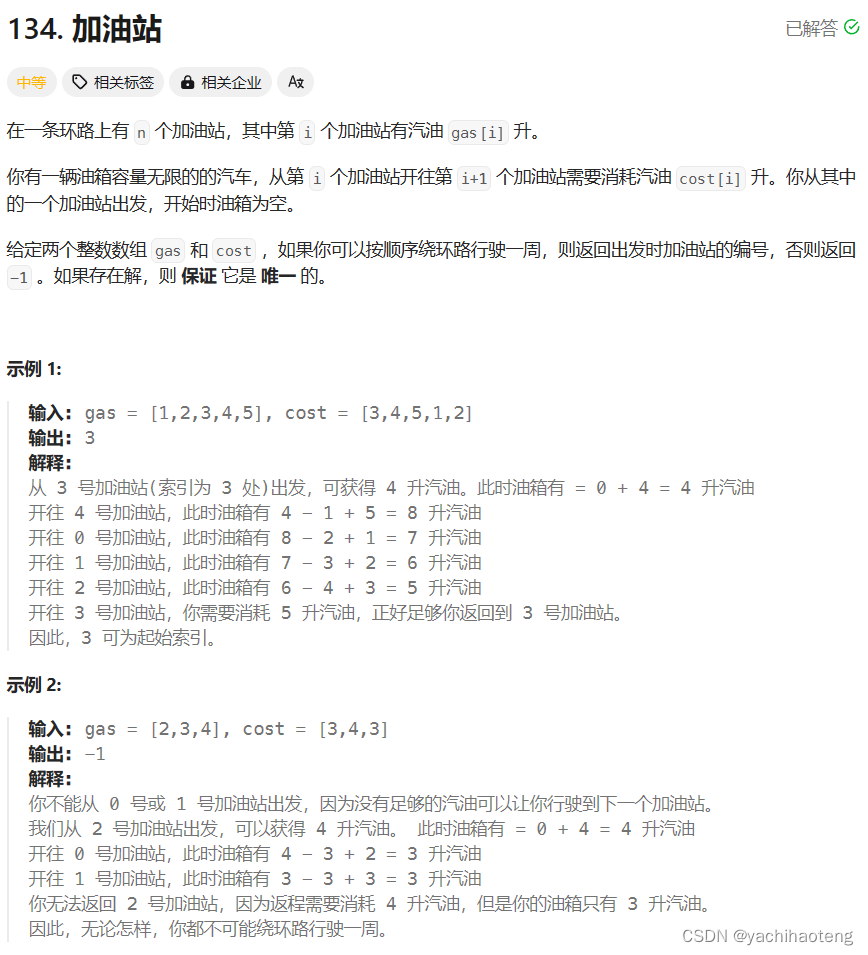
学习:本题其实很容易发现gas数组和cost数组的差,就是该站点结余的油量,我们在移动过程中理应让油量始终保持为正。因此本题的思考逻辑就是从某个站点出发,如果油量小于0则说明该点不能环路行驶一圈,反则则可以。
解法一:暴力解法,暴力遍历每个节点环行一周的结果。(力扣超时)
注意:for循环适合模拟从头到尾的遍历,而while循环适合模拟环形遍历,因此对于本题的场景需要使用while进行环行循环要十分注意。
//时间复杂度O(n^2)
//空间复杂度O(1)
class Solution {
public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {for (int i = 0; i < cost.size(); i++) {int rest = gas[i] - cost[i]; // 记录剩余油量int index = (i + 1) % cost.size();while (rest > 0 && index != i) { // 模拟以i为起点行驶一圈(如果有rest==0,那么答案就不唯一了)rest += gas[index] - cost[index];index = (index + 1) % cost.size();}// 如果以i为起点跑一圈,剩余油量>=0,返回该起始位置if (rest >= 0 && index == i) return i;}return -1;}
};解法二:贪心
贪心策略为:首先只有在总油量减去总消耗大于等于0的时候,才说明可以跑完一圈。其次我们在环行的过程中,还需要保持剩油量是正的,才能够继续行驶下去。因此我们可以 i 从0开始累加每个站点的剩油量(gas[i] - cost[i]),一旦累加和小于零,则说明[0, i]区间都不能作为起始位置,因为这个区间选择任何一个位置作为起点,到i这里都会断油(一定不会说从中间开始某个点不会断油,因为如果是那样的话后半部分为正,那前半部分一定为负,也会使得满足剩油量为负的条件,跳到i+1),那么起始位置从i+1算起,再从0计算剩油量。
那么局部最优:当前累加rest[i]的和curSum一旦小于0,起始位置至少要是i+1,因为从i之前开始一定不行。全局最优:找到可以跑一圈的起始位置。
代码:
//时间复杂度O(n)
//空间复杂度O(1)
class Solution {
public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {//贪心,局部最优找到累加为正的地方int count = 0; //计算总和,总和小于0说明无法环路一周int idcount = 0; //计算当前i往后的总和,该总和小于0说明不能从i出发int index = 0; //找到正确的出发下标for(int i = 0; i < gas.size(); i++) {int rest = gas[i] - cost[i];count += rest;idcount += rest;if(idcount < 0) { // 当前累加rest[i]和 curSum一旦小于0idcount = 0; // idcount从0开始计算index = i + 1; //起始位置更新为i+1}}if(count < 0) return -1;return index;}
};135. 分发糖果
文档讲解:代码随想录分发糖果
视频讲解:手撕分发糖果
题目:

学习:本题属于贪心算法中两个维度的问题,也就是需要两次贪心分别处理两种情况。本题中我们对于一个孩子来说,即要考虑他的左边和他的大小关系,又要考虑他的右边和他的大小关系,这就是我们要处理的两个问题。对于这种情况而言,我们需要将这两个问题分开解决,先考虑每个孩子右边比自身大的情况,再考虑每个孩子左边比自身大的情况,不能同时考虑,否则就会顾此失彼。
首先考虑右边孩子评分大的情况,从前向后遍历。此时的局部最优为:只要右边评分比左边大,右边的孩子就多一个糖果。全局最优为:相邻的孩子中,评分高的右孩子获得比左边孩子更多的糖果。
接着我们再确定左边孩子评分大的情况,从后往前遍历。此时的局部最优就为:只要左边评分比右边大,左边的孩子就多一个糖果。全局最优为:相邻的孩子中,评分高的左孩子获得比右边孩子更多的糖果。(这个地方要注意,再更新评分更高的孩子的时候,我们要判断此时更新的值和原本的值谁更大,因为原本的值是保证了他和他左边孩子的关系,因为谁更大取谁,这样就能够同时保证左右孩子的关系了。
代码:
//时间复杂度O(n)
//空间复杂度O(n)
class Solution {
public:int candy(vector<int>& ratings) {//两次贪心vector<int> candys(ratings.size(), 1); //初始化先给每个小孩一个糖果//第一次贪心,从左向右,先遍历右孩子比左孩子大的情况,局部最优:右孩子比左孩子大就多一个糖果for(int i = 1; i < ratings.size(); i++) {if(ratings[i] > ratings[i - 1]) {candys[i] = candys[i - 1] + 1;}}//第二次贪心,从右向左,遍历左孩子比右孩子大的情况,局部最优:左孩子比右孩子大就多一个糖果for(int i = ratings.size() - 2; i >= 0; i--) {if (ratings[i] > ratings[i + 1]) {//这里要注意要去当前值和右孩子加1之间的最大值,这样才能保证该点同时大于左右孩子。candys[i] = max(candys[i], candys[i + 1] + 1); }}//求和int result = 0;for(int i = 0; i < candys.size(); i++) {result += candys[i];}return result;}
};860.柠檬水找零
文本讲解:代码随想录柠檬水找零
视频讲解:手撕柠檬水找零
题目:

学习:本题看起来题干很多很复杂,但实际上就是每位顾客花5美元买柠檬水,但这个过程中会出现三种情况分别是:1.顾客给了5美元,不需要找钱;2.顾客给了10美元,需要找5美元给顾客;3.顾客给了20美元,需要找15美元给顾客。针对这三种情况我们可以逐个分析。
1.顾客给了5美元:对于这种情况,我们不需要找钱的同时,我们手里还多了一张5美元。
2.顾客给了10美元,需要找5美元:对于这种情况,需要我们手头上有至少一张5美元,否则我们就不能正确找零返回false。如果我们手头上有至少一张5美元,则我们减少一张5美元,多一张10美元。
3.顾客给了20美元,需要找15美元:对于这种情况,就是需要我们进行贪心算法的时候了,因为对于我们来说5美元既可以给10美元的顾客找钱,又可以给20美元的顾客找钱。因此我们在给20美元的顾客找钱的时候应优先消耗美元10,保留更加万能的5美元,这样才能更好的进行正确的找零。因此有三种情况:1.手头上有10美元,5美元,则减少一张10美元,一张5美元;2.手头上美元10美元,但5美元大于3张,则减少3张5美元;3.手头上凑不出15美元的数(注意两张10美元不行)返回false。
代码:根据以上三种情况,则可编写代码
//时间复杂度O(n)
//空间复杂度O(1)
class Solution {
public:bool lemonadeChange(vector<int>& bills) {//记录手头上5美元和10美元的数量,20美元的不需要记录,因为20没有不能用于找钱int count5 = 0;int count10 = 0;for(int i = 0; i < bills.size(); i++) {//分别处理收到三种钱的情况if(bills[i] == 5) {count5++;}if(bills[i] == 10) {if(count5 == 0) {return false;}count5--;count10++;}//第三种情况需要进行贪心//贪心策略:如果有10元钞票优先找10元钞票,因为5元钞票比10元钞票更万能if(bills[i] == 20) {if(count10 > 0 && count5 > 0) {count10--;count5--;}else if(count5 >= 3) {count5 -= 3;}else {return false;}}}return true;}
};406.根据身高重建队列
文档讲解:代码随想录根据身高重建队列
视频讲解:手撕根据身高重建队列
题目:
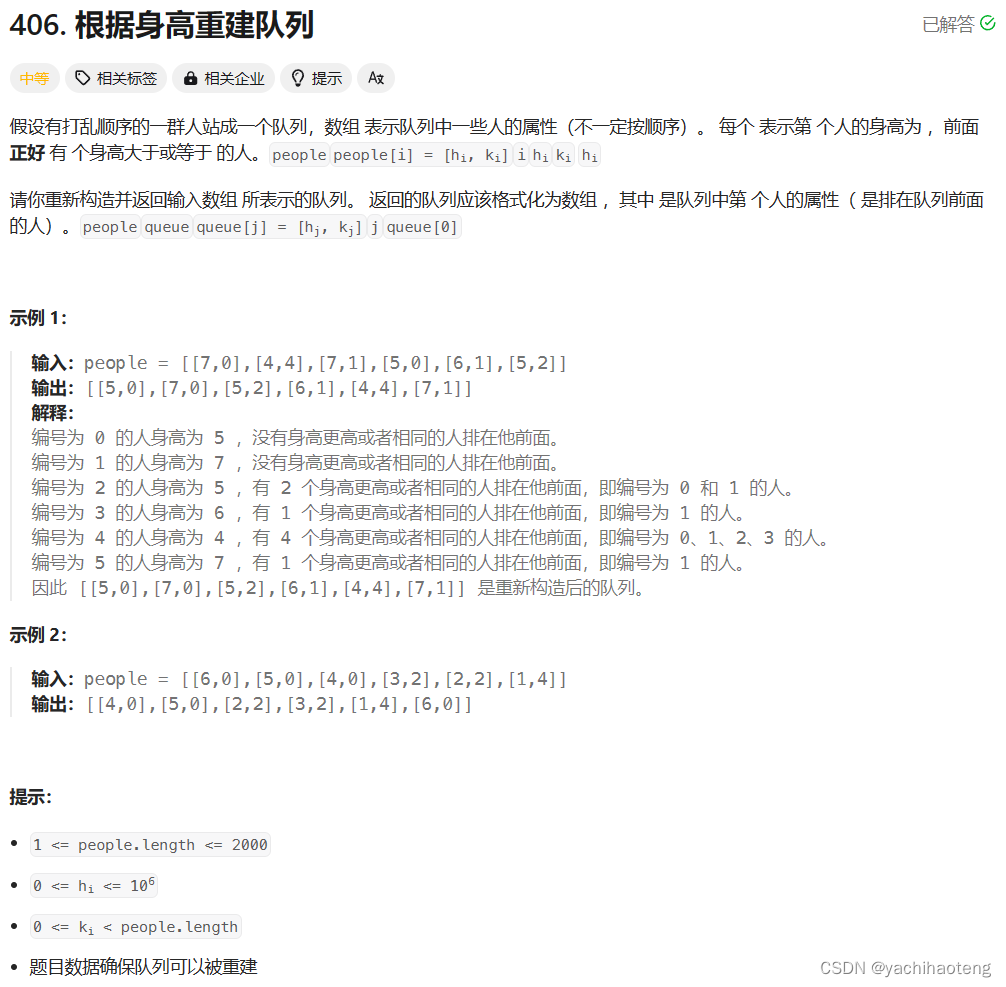
学习:本题与分发糖果相同,同样都是两维问题,我们需要分别考虑身高和前面身高大于等于的人的数量这两个因素。不能两个维度一起考虑,一定会出现顾此失彼的情况。
本题中如果我们需要对数组先进行排序,来解决一个维度上的问题。如果我们选择对k(身高大于等于的数量)进行排序,会发现最后得到的数组会发现k的排列不符合条件,身高也不符合条件,两个维度都没办法确定下来(这是因为会存在部分身高很高,因此k为0的干扰)。
因此本题我们需要先对身高进行排序,身高从高到低进行排序,这样也会有个好处,排序之后,如果后面的位置出现问题需要前插,也不会影响前面的数的排序,因为后面的数一定比前面的数小,不会影响到k值。
因此本题的贪心就是:局部最优:优先按身高高的people的k来插入。插入操作过后的people满足队列属性;全局最优:最后都做完插入操作,整个队列满足题目队列属性。
代码:
//时间复杂度O(nlogn + n^2)
//空间复杂度O(n)
class Solution {
public:static bool camp(vector<int>&a, vector<int>&b) {//身高从大到小排列,便于进行插入处理if(a[0] != b[0]) {return a[0] > b[0];}else { //如果身高一样,让其前面身高少的排前面return a[1] < b[1];}}vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {//对数组进行排序,让身高高的先排前面,这样我们就能依据前面身高的数量,来插入每一个数sort(people.begin(), people.end(), camp);//贪心策略,遍历数组,优先按照身高高的people的k来进行插入,这样也就不用担心后续身高矮的插入造成影响vector<vector<int>> queue; //这里不能初始化数组的大小,因为后续要采用插入进行操作for(int i = 0; i < people.size(); i++) {int index = people[i][1]; //确定要插入的位置queue.insert(queue.begin() + people[i][1], people[i]);}return queue;}
};本题中存在一个问题,使用vector是非常费时的,C++中vector(可以理解是一个动态数组,底层是普通数组实现的)如果插入元素大于预先普通数组大小,vector底部会有一个扩容的操作,即申请两倍于原先普通数组的大小,然后把数据拷贝到另一个更大的数组上。所以使用vector(动态数组)来insert,是费时的,插入再拷贝的话,单纯一个插入的操作就是O(n^2)了,甚至可能拷贝好几次,就不止O(n^2)了。
代码:因此本题可以采用list类来保存数组,虽然时间复杂度没变,但实际效率是增加了的。
class Solution {
public:// 身高从大到小排(身高相同k小的站前面)static bool cmp(const vector<int>& a, const vector<int>& b) {if (a[0] == b[0]) return a[1] < b[1];return a[0] > b[0];}vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {sort (people.begin(), people.end(), cmp);list<vector<int>> que; // list底层是链表实现,插入效率比vector高的多for (int i = 0; i < people.size(); i++) {int position = people[i][1]; // 插入到下标为position的位置std::list<vector<int>>::iterator it = que.begin();while (position--) { // 寻找在插入位置it++;}que.insert(it, people[i]);}return vector<vector<int>>(que.begin(), que.end());}
};