一、题目

1、题目描述

2、输入输出

2.1输入

2.2输出

3、原题链接

633F - The Chocolate Spree

---

二、解题报告

1、思路分析

2600的题，但是不算很困难。

先考虑暴力做法，如何得到两条不相交的路径？

枚举删除的边，得到两棵子树，分别在两棵子树上进行dfs找最长路径

时间复杂度O(N^2)

考虑优化：换根dp

为什么能想到换根dp？

考虑答案可能“长什么样子”：
1、两条路径分别在两个不相交子树中，此时，我们利用类似树的直径的求法，一次dfs就能搞定

答案就是两个 /\

2、两条路径在两棵相交子树中

这个时候答案长这个样子：

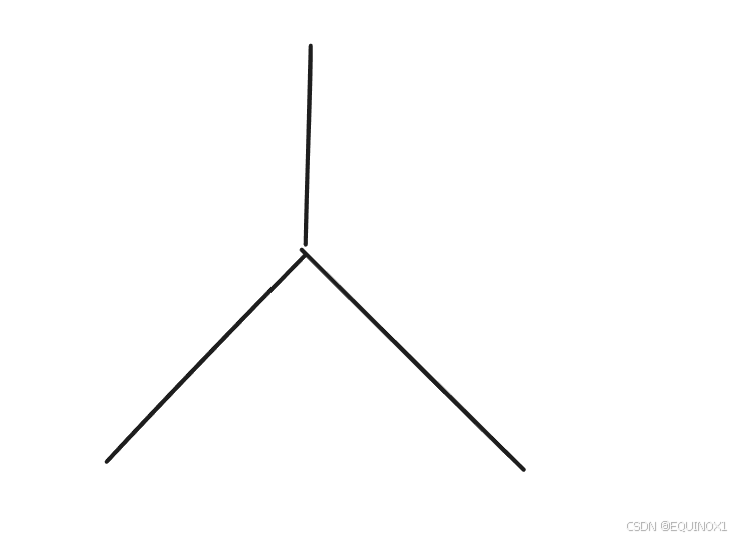
显然是由三段拼接而来的

对于根节点u，我们考虑固定子树v内的最长一段，然后考虑另外两段怎么选：

子树v1内的一段

子树v2内的一段

u向上的某段

从这三段中选两段

显然要维护根节点子树的最大值、次大值、次次大值

这个我们可以靠换根dp来进行维护

2、复杂度

时间复杂度： O(N)空间复杂度：O(N)

3、代码详解

 ​

#include <bits/stdc++.h>
using i64 = long long;
using i128 = __int128;
using PII = std::pair<int, int>;
const int inf = 1e9 + 7, P = 998244353;struct Node {i64 fi, se, th, fiv, sev;  
};void solve() {int n;std::cin >> n;std::vector<int> a(n);std::vector<std::vector<int>> g(n);for (int i = 0; i < n; i ++ ) std::cin >> a[i];for (int i = 1, u, v; i < n; i ++ ) {std::cin >> u >> v;-- u, -- v;g[u].push_back(v), g[v].push_back(u);}std::vector<i64> subAns(n);std::vector<Node> nodes(n);i64 res = 0;auto dfs1 = [&](auto&& self, int u, int fa) -> i64 {subAns[u] = a[u];i64 maxS = a[u], maxSubAnsV = 0;Node& p = nodes[u];for (int v : g[u]) {if (v == fa) continue;i64 s = self(self, v, u);res = std::max(res, maxSubAnsV + subAns[v]);maxSubAnsV = std::max(maxSubAnsV, subAns[v]);subAns[u] = std::max(subAns[u], maxS + s);maxS = std::max(maxS, s + a[u]);if (s > p.fi) {p.th = p.se, p.se = p.fi, p.fi = s;p.sev = p.fiv, p.fiv = v;}else if (s > p.se) {p.th = p.se, p.se = s;p.sev = v;}else if(s > p.th)p.th = s;}subAns[u] = std::max(subAns[u], maxSubAnsV);return maxS;};dfs1(dfs1, 0, -1);auto dfs2 = [&](auto&& self, int u, int fa, i64 maFa) -> void {Node& p = nodes[u];for (int v : g[u]) {if (v == fa) continue;if (v == p.fiv) {res = std::max(res, subAns[v] + a[u] + p.se + std::max(p.th, maFa));self(self, v, u, a[u] + std::max(p.se, maFa));}else {i64 s = p.se;if (v == p.sev) s = p.th;res = std::max(res, subAns[v] + a[u] + p.fi + std::max(s, maFa));self(self, v, u, a[u] + std::max(p.fi, maFa));}}};dfs2(dfs2, 0, -1, 0);std::cout << res;
}int main(int argc, char** argv) {std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);int _ = 1;// std::cin >> _;while (_ --)solve();return 0;
}