目录
- 1. Linux线程概念
- 什么是线程
- 2. 线程的优点
- 3. 线程的缺点
- 4. 线程异常
- 5.线程用途
- 6. Linux进程VS线程
1. Linux线程概念
什么是线程
- 在一个程序里的一个执行路线就叫做线程(thread)。更准确的定义是:线程是“一个进程内部的控制序列”
- 一切进程至少都有一个执行线程
- 线程在进程内部运行,本质是在进程地址空间内运行
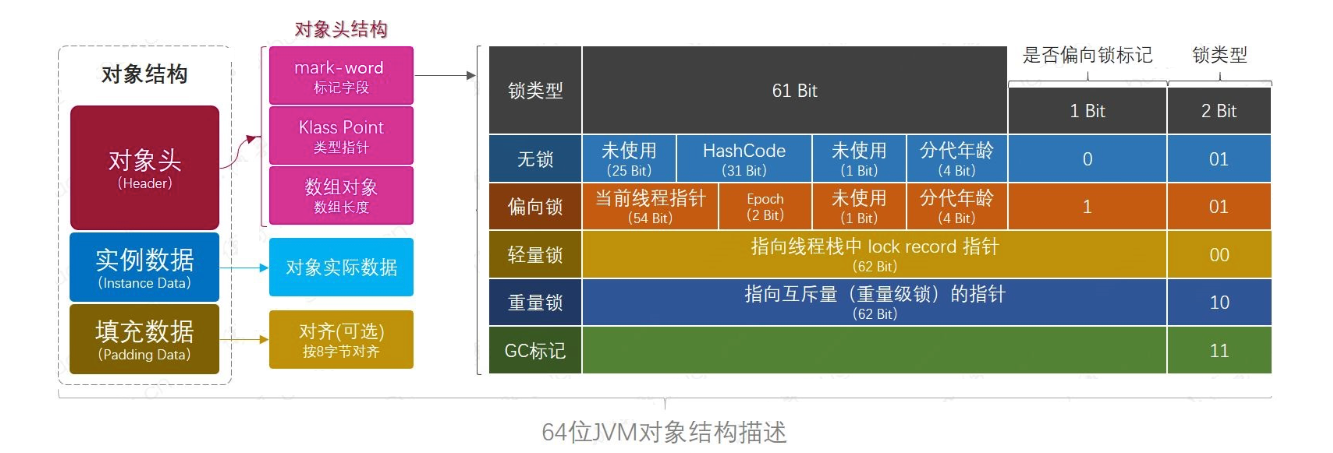
- 在Linux系统中,在CPU眼中,看到的PCB都要比传统的进程更加轻量化
- 透过进程虚拟地址空间,可以看到进程的大部分资源,将进程资源合理分配给每个执行流,就形成了线程执行流
课本上对于线程的解释为
- 线程是比进程更加轻量化的一种执行流
- 线程是在进程内部执行的一种执行流
- 线程是CPU调度的基本单位
- 进程是承担系统资源的基本实体
这里我们怎么理解呢?
在Linux下的进程在创建时就会生成一个task_struct,然后再task_struct中的指针指向虚拟内存中的虚拟地址空间,虚拟地址空间通过页表映射就可以找到当前进程的在物理内存中的数据段以及代码段
- 如下就是我们之前讲进程的图

不了解task_struct的小伙伴,我在这里做一下科普
Task_struct通常是在Linux内核中用于描述进程任务信息的数据结构。它是一个重要的系统级数据结构,包含了关于每个正在运行或就绪的任务的各种属性,如任务的状态、堆栈指针、CPU上下文、优先级等关键信息。通过这个结构体,操作系统能够管理和调度各个进程。
- 当我们进程中有了多线程之后

我先把图展示出来,我们讲解一下再来看这个图会有不用的理解
轻量级如何理解?
- 其实轻量级也就是,其实Linux中是按照执行流来划分的,也就是说一个线程就是一个执行流,而我们之前讲的进程其实也就是一个线程在执行,那么就是进程里只有一个线程在运行我们就叫他单进程,这样的话,其实进程中可以有多个线程在运行,那么就是多个执行流。也就是说,轻量级的含义就是他是以执行流来划分,而不是一整个进程
- 之前讲的进程可以视作为内部只有一个执行流的进程
- 今天所接触的也就是内部有多个执行流的进程
- 所以线程是在进程内部执行的一种执行流
- 进程在执行的时候如果有多线程,那么就会将它的时间片以及资源划分给这多个线程进行执行,而这多个线程也就组成了这个进程
2. 线程的优点
- 创建一个新线程的代价要比创建一个新进程小得多
- 与进程之间的切换相比,线程之间的切换需要操作系统做的工作要少很多
- 线程占用的资源要比进程少很多
- 能充分利用多处理器的可并行数量
- 在等待慢速I/O操作结束的同时,程序可执行其他的计算任务
- 计算密集型应用,为了能在多处理器系统上运行,将计算分解到多个线程中实现
- I/O密集型应用,为了提高性能,将I/O操作重叠。线程可以同时等待不同的I/O操作
3. 线程的缺点
- 性能损失
一个很少被外部事件阻塞的计算密集型线程往往无法与共它线程共享同一个处理器。如果计算密集型线程的数量比可用的处理器多,那么可能会有较大的性能损失,这里的性能损失指的是增加了额外的同步和调度开销,而可用的资源不变。
- 健壮性降低
编写多线程需要更全面更深入的考虑,在一个多线程程序里,因时间分配上的细微偏差或者因共享了不该共享的变量而造成不良影响的可能性是很大的,换句话说线程之间是缺乏保护的。
- 缺乏访问控制
进程是访问控制的基本粒度,在一个线程中调用某些OS函数会对整个进程造成影响。
- 编程难度提高
编写与调试一个多线程程序比单线程程序困难得多
4. 线程异常
- 单个线程如果出现除零,野指针问题导致线程崩溃,进程也会随着崩溃
- 线程是进程的执行分支,线程出异常,就类似进程出异常,进而触发信号机制,终止进程,进程终止,该进程内的所有线程也就随即退出
5.线程用途
- 合理的使用多线程,能提高CPU密集型程序的执行效率
- 合理的使用多线程,能提高IO密集型程序的用户体验(如生活中我们一边写代码一边下载开发工具,就是多线程运行的一种表现)
6. Linux进程VS线程
- 进程是资源分配的基本单位
- 线程是调度的基本单位
- 线程共享进程数据,但也拥有自己的一部分数据:
- 线程ID
- 一组寄存器
- 栈
- errno
- 信号屏蔽字
- 调度优先级
进程的多个线程共享 同一地址空间,因此Text Segment、Data Segment都是共享的,如果定义一个函数,在各线程中都可以调用,如果定义一个全局变量,在各线程中都可以访问到,除此之外,各线程还共享以下进程资源和环境:
- 文件描述符表
- 每种信号的处理方式(SIG_ IGN、SIG_ DFL或者自定义的信号处理函数)
- 当前工作目录
- 用户id和组id
进程和线程的关系如下图: