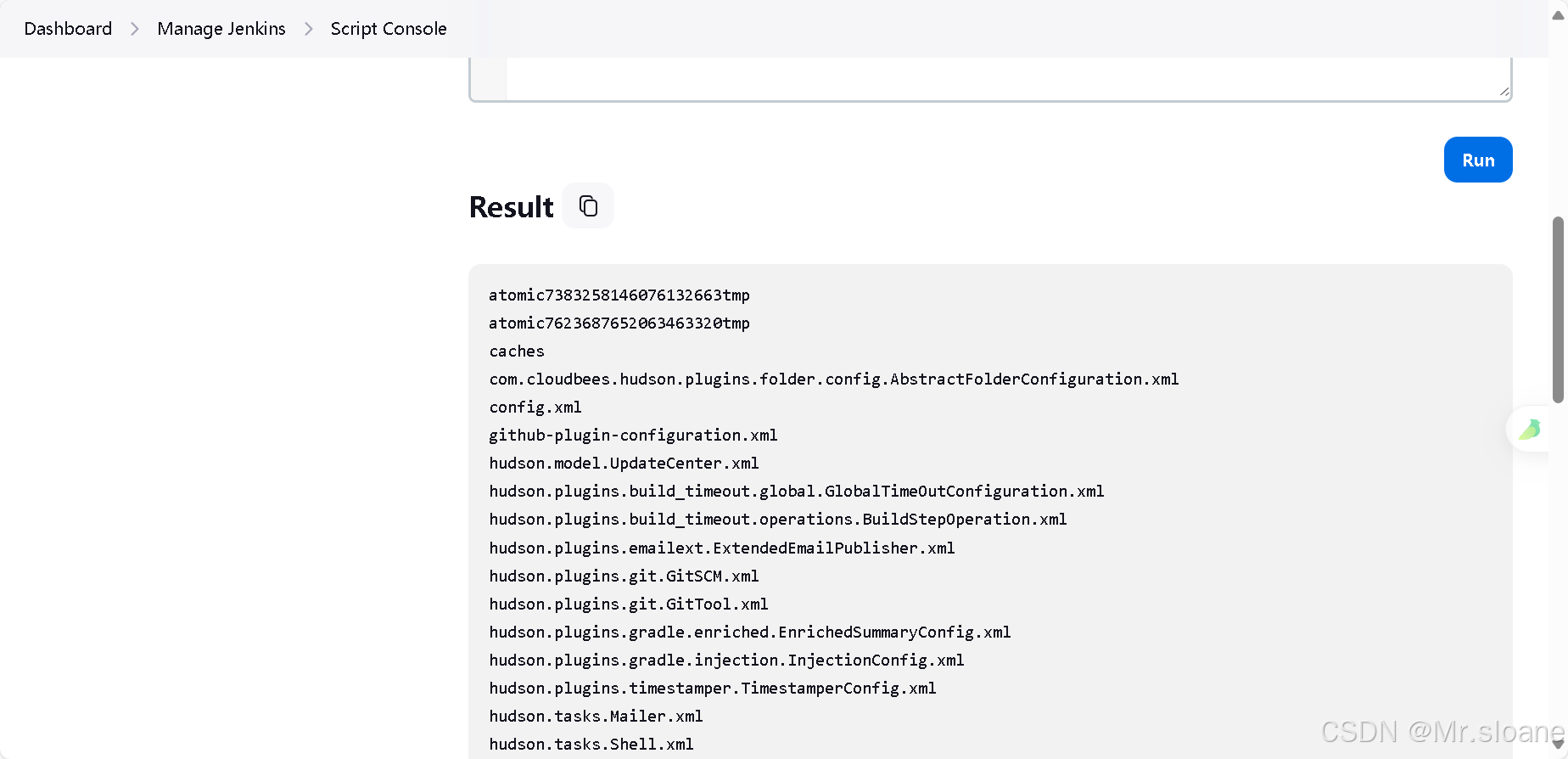
1.机器学习定义：

机器学习就是让机器从大量的数据集中学习，进而得到一个更加符合现实规律的模型，通过对模型的使用使得机器比以往表现的更好

2.监督学习：

从给定的训练数据集中学习出一个函数（模型参数），当新的数据到来时，可以根据这个函数预测结果。监督学习的训练集要求包括输入输出，也可以说是特征和目标。训练集中的标签是由人标注的。监督学习就是最常见的分类（注意和聚类区分）问题，通过已有的训练样本（即已知数据及其对应的输出）去训练得到一个最优模型，再利用这个模型将所有的输入映射为相应的输出，对输出进行简单的判断从而实现分类的目的。也就具有了对未知数据分类的能力。监督学习的目标往往是让计算机根据已有的数据集去学习我们已经创建好的分类系统，知道输入和输出结果之间的关系。根据这种已知的关系，训练得到一个最优的模型。也就是说，在监督学习中训练数据既有特征(feature)又有标签(label)，通过训练，让机器可以自己找到特征和标签之间的联系，在面对只有特征没有标签的数据时，可以判断出标签。通俗一点，可以把机器学习理解为我们教机器如何做事情。

即从正确答案中学习，数据同时有输入x和输出标签y

分为回归和分类

回归：从哪个无限多可能的输出数字中预测数字，有无限输出。例如房价预测

分类：对一个类别进行预测，所有小部分的一个产出。分类只有少量输出、离散的有限的。例如预测是否为肿瘤

3.无监督学习：

输入数据没有被标记，也没有确定的结果。样本数据类别未知，需要根据样本间的相似性对样本集进行分类（聚类，clustering）试图使类内差距最小化，类间差距最大化。

即计算机自己决定结果如何，数据仅仅带有输入x，没有输出标签y，且算法必须找出数据的结构

聚类：获取没有标签的数据并尝试自动将它们分组到集群中

4.定义：

训练集：用于训练计算机的数据集合（监督学习包括输入特征和输出目标）

输入变量：x

输出目标：y

训练示例的总数：m

第i个样例：(𝑥𝑖,𝑦𝑖)

模型：f

输出预测：y

归纳偏好：机器学习算法在学习过程中对某种类型假设的偏好，称为“归纳偏好”

5.经验误差与过拟合

误差：学习器的实际预测输出与样本的真实输出之间的差异称为“误差”(error)

经验误差：学习器在训练集上的误差称为“训练误差”(training  error)或 “经验误差” (empirical error),

泛化误差：在新样本上的误差称为“泛化误差”(generalizationerror).

过拟合：当学习器把训练样本学得“太好” 了的时候，很可能已经把训练样本自身的一些特点当作了所有潜在样本都会具有的一般性质，这样就会导致泛化性能下降。无法彻底避免

因素：学习能力过于强大

欠拟合：指对训练样本的一般性质尚未学好

因素：学习能力低下

6.评估方法：

测试集应该尽可能与训练集互斥即测试样本尽量不在训练集中出现、未在训练过程中使用过.

• 留出法：
  • “留出法”(hold-out)直接将数据集。划分为两个互斥的集合，其中一个集合作为训练集S ,另一个作为测试集T ,即0  = S U T, S n T = 0.在S上训练出模型后，用T来评估其测试误差，作为对泛化误差的估计.
  • 训练/测试集划分要荆轲能保持数据分布的一致性
  • 分层采样：保留类别比例的采样方式
  • 单次使用留出法得到的估计结果往往不够稳定可靠，使用留出法时一般采用若干次随即划分、重复进行实验评估后取平均值作为留出法的评估结果
  • 常见做法是将大约2/3〜4/5的样本用于训练，剩余样本用于测试
• 交叉验证法
  • “交叉验证法”(cross  validation)先将数据集D划分为k个大小相似的互斥子集，即

• 每个子集D i都尽可能保持数据分布的一致性，即从。中通过分层采样得到.然后，每次用k - 1个子集的并集作为训练集，余下的那个子集作为测试集；这样就可获得k组训练/测试集，从而可进行k次训练和测试，最终返回的是这k个测试结果的均值.
• 
• 为减小因样本划分不同而引入的差别，k折交叉验证通常要随机使用不同的划分重复p次，最终的评估结果是这p 次 k折交叉验证结果的均值
• 留一法：
  • 假定数据集D中包含m个样本，若令k  =小，则得到了交叉验证法的一个特例：留一法(Leave-One-Out,简称L O O )
  • 绝大多数情况下，留一法的评估结果比较准确
  • 缺陷：数据集较大时，训练m个模型不符合实际

• 自助法：
  • 给定包含 m 个样本的数据集。，我们对它进行采样产生数据集D𝚤每次随机从D中挑选一个样本,将其拷贝放入D𝚤 ,然后再将该样本放回初始数据集D中,使得该样本在下次采样时仍有可能被采到；这个过程重复执行m次后，我们就得到了包含m个样本的数据集D𝚤 ,这就是自助采样的结果
  • 通过自助采样，初始数据集。中约有36.8%的样本未出现在采样数据集D𝚤中.
  • 包外估计：
    • 将D𝚤用作训练集，D\D𝚤用作训练集，实际评估的模型与期望评估的模型都使用m个训练样本，而我们仍有数据总量月1/3，没在训练集出现的样本用于测试
  • 适用于数据集较小，难以有效划分训练/测试集，对于集成学习有好处
  • 缺点：改变了初始数据集的分布，引入估计偏差
• 调参与最终模型
  • 调参：对算法参数进行设定
  • 显示做法是对每个参数选定一个范围和变化步长
  • 最终模型：在模型选择完成后，学习算法和参数配置已经选定，此时用数据集D重新训练模型。这个模型使用全部m个样本，这就是最终模型。
  • 验证集：模型评估与选择中用于评估测试的数据集

7.性能度量：

定义：衡量模型泛化能力的评价标准

• 均方误差：回归任务常用的性能度量
  • 
  • 对于数据分布𝒟和概率密度函数p(⋅)
    • 
• 错误率：分类错误的样本数占样本总数的比例
• 精度：分类正确的样本数占样本总数的比例
  • 
  • 对于数据分布𝒟和概率密度函数p(⋅)
    • 

• 

• 查准率、查全率：
  • 对于二分类问题：
    • 可将样例根据其真实类别与学习器预测类别的组合划分为真正例(true positive)> 假正例(false positive)> 真反例(true negative)>假反例(false negative)四种情形，令TP、F P、T N、F N分别表示其对应的样例数，则显然有T P  +  F P  +  T N  +  F N =样例总数.
      • 

• 查准率和查全率是矛盾的度量，查准率越高，查全率越低，反之亦然
• P-R曲线
  • 
  • 排在前面的最可能是正例的样本，最后的是最不可能的是正例的样本，按此顺序把样本作为正例进行预测，计算查全率、查准率，将查全率作为x轴，查准率作为y轴
  • 若一个学习器的P-R曲线被另一个学习器的曲线完全包住，则断言后者性能优于前者
  • 若发生交叉，则难以断言孰优孰劣，此时判断方法为比较曲线下面积，表示了学习去在查准率和查全率取得“双高”的比例
  • 平衡点：查全率=查准率时的取值，上图A优于B
  • F1度量：
    • 
  • F𝛽：F1度量的一般形式，表达出对查准率/查全率的不同偏好
    • 

𝛽>0度量查全率对查准率的相对重要性，

𝛽=1退化为标准的F1

𝛽>1查全率有更大影响

𝛽<1查准率有更大影响

• 希望在n个二分类混淆矩阵上综合考察查准率和查全率
  • 宏查准率：macro-P
  • 宏查全率：macro-R
  • 宏F1：macro-F1
    • 
  • 微查准率：micro-P
  • 微查全率：micro-R
  • 微F1：micro-F1
    • 

• 

• ROC与AOC：
  • 正类：大于分类阈值
  • 反类：小于分类阈值
  • 排序质量的好坏体现了综合考虑学习器在不同任务下的“期望泛化性能”的好坏---ROC曲线
    • 我们根据学习器的预测结果对样例进行排序，按此顺序逐个把样本作为正例进行预测，每次计算出两个重要量的值，分别以它们为横、纵坐标作图，就得到了 “R O C曲线”，横轴是假正例率FPR，纵轴是真正例率TPR
      • 

• 

• 比较：如果一个学习器的ROC曲线被另一个学习器完全包住，则后者性能优于前者。
  • 若发生交叉，则无法断定孰优孰劣
  • 若一定要进行比较，则比较曲线下面积AUC
    • 
  • 给定m +个正例和m -个反例，令D +和D -分别表示正、反例集合,则排序“损失”(loss)定义为：对应的是ROC曲线之上的面积
    • 

• 
• 

• 

• 代价敏感错误率与代价曲线：
  • 非均等代价：为权衡不同类型错误造成的损失
  • 二分类任务的代价矩阵：

• 代价敏感错误率：
  • D+与D-分别表示样例集D的正例子集和反例子集
  • 
• 代价曲线：
  • 非均等代价下，反映学习器的期望总体代价
  • 横轴是取值为[0，1]的正例概率代价，p是正例的概率
  • 
  • 纵轴是取值为[0，1]的归一化代价，FPR是假正例率，FNR=1-TPR是反假例率，cost01​ 是将正例误判为负例的代价，cost10​ 是将负例误判为正例的代价
  • 
  • 画法：代价曲线的绘制很简单：ROC曲线上每一点对应了代价平面上的一条线段，设ROC曲线上点的坐标为(TPR,FPR),则可相应计算出FNR,然后在代价平面上绘制一条从(0,FPR)到(1,FNR)的线段，线段下的面积即表示了该条件下的期望总体代价；如此将ROC曲线上的每个点转化为代价平面上的一条线段，然后取所有线段的下界，围成的面积即为在所有条件下学习器的期望总体代价，
  • 

8.比较检验:

• 假设检验：
  • “假设”是指对学习器泛化错误率分布的某种判断或猜想，可根据测试错误率估推出泛化错误率的分布
  • 泛化错误率为𝜀的学习器被测得测试错误率为𝜀的概率
  • 
  • P（𝜀；𝜀）在𝜀=𝜀时最大，| 𝜀−𝜀|增大时减小。
  • 
• 一个数据集上比较两个算法的性能：
  • 交叉验证t检验：
    • 
    • 
    • 小于临界值（自由度为k-1的t分布上尾部累积分布为𝛼/2的临界值）
    • 
    • 则假设不能被拒绝，否则认为两个学习器性能有显著差别，且平均错误率小的性能优
    • 5×2交叉验证：
      • 
  • McNemar检验：
    • 
    • 若我们做的假设是两学习器性能相同，则应有e01 =  e10,那么变量|e01 -  e10|应当服从正态分布，且均值为1,方差为e01 + e10.因此变量
    • 
    • 服从自由度为1的𝜒2分布，即标准正态分布变量的平方.给定显著度必当以上变量值小于临界值𝜒𝛼2时，不能拒绝假设，即认为两学习器的性能没有显著差别；否则拒绝假设，即认为两者性能有显著差别，且平均错误率较小的那个学习器性能较优.自由度为1的𝜒2检验的临界值当𝛼 = 0.05时为3.8415,𝛼 = 0.1时为 2.7055.
• 一组数据集上对多个算法进行比较
  • 基于排序的Friedman检验：
    • 假定我们用。1、0 2、。3和 。4四个数据集对算法A、B、C进行比较.首先，使用留出法或交叉验证法得到每个算法在每个数据集上的测试结果，然后在每个数据集上根据测试性能由好到坏排序,并赋予序值1,  2,若算法的测试性能相同，则平分序值.
    • 

• 
• 上述式子k和N较大时，服从自由度为k-1的𝜒2分布
• 
• 𝜏𝐹服从自由度为k-1和(k-1)(N-1)的F分布
• 

• Nemenyi后续检验：
  • 若算法性能显著不同，需要进行后续检验进一步区分算法-----Nemenyi检验计算出平均序值差别的临界值域
  • 

• 
• 若两个算法的平均序值之差超出了临界值域CD，则以相应的置信度拒绝“两个算法性能相同”

• Friedman检验图中纵轴显示各个算法，横轴是平均序值.对每个算法,用一个圆点显示其平均序值，以圆点为中心的横线段表示临界值域的大小.然后就可从图中观察，若两个算法的横线段有交叠，则说明这两个算法没有显著差别，否则即说明有显著差别.
• 

9.线性回归网课

计算误差：

目标是找到参数w或w和b，使成本函数J的值最小

J越小的越拟合

实现梯度下降：

梯度下降(Gradient descent)是一个用来求函数极小值的算法，将使用梯度下降算法来求出代价函数J(w,b)的最小值。

=

实现同时更新的梯度下降：

𝛼：学习率，

用来控制梯度下降时的步长。若α 很大，则说明梯度下降会很迅速；若α 很小，则说明梯度下降会很缓慢。并且上式中w​,b需同时更新

线性回归：

• 通过属性的线性组合进行预测的函数：
  • 即f （x ） =  W1X1 +  W2X2 +  • • • +  WdXd +  b ,，一般向量形式写为：𝜔Τx+b
• 若属性值存在“序”关系，可通过连续化将其转化为连续值，例如身高“高、中、低”可转化为1.0，0.5，0“
• 若属性值间不存在序关系，假定有k个属性，则通常转化为k维向量，例如属性”瓜类“取值”西瓜、南瓜、黄瓜“，可转化为(0,0,1),(0,1,0),(1,0,0)
• 均方误差：
  • 
• 最小二乘”参数估计“：求解𝜔被b使E𝜔，b=𝑖=1𝑚（𝑦𝑖−𝜔𝑥𝑖+𝑏）2最小化的过程
• 𝜔和b的最优解的闭式解
  • 

• 

• 多元线性回归：
  • 样本由d个属性描述
  • 试图学得：
    • f(𝑥𝑖)=𝜔Τ𝑥𝑖+b，使得f(𝑥𝑖)≅𝑦𝑖
  • 
• 广义线性模型：
  • 
  • 函数g()被称为联系函数
• 分类任务：
  • 
  • 若预测值z>0则判定为正例，z<0判定为反例，预测值为临界值0可任意判别
  • 
• y=11+e−(𝜔Τx+𝑏)
• 几率：将y视为样本x作为正例的可能性，1-y是视为反例的可能性，几率为y1−y，翻译了x作为正例的相对可能性
• 线性判别分析（LDA）：
  • 给定训练样例集，设法将样例投影到一条直线上,使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离；在对新样本进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定新样本的类别
  • 主要目标：
    • 分类：通过找到最佳的投影方向来最大化不同类之间的分离度，从而帮助分类。
    • 降维：在保持类别可分性的前提下减少数据集的维度
  • 
  • .欲使同类样例的投影点尽可能接近，可以让同类样例投影点的协方差尽可能小，即
    • 
    • 尽可能小；而欲使异类样例的投影点尽可能远离,可以让类中心之间的距离尽可能大，即
    • 
    • 尽可能大，同时考虑二者，则可得到欲最大化的目标
    • 
  • 类间散度矩阵：
    • 
    • 则J可写为：（广义瑞利商）
    • 

• 

• LDA步骤：
  • 计算类内散度矩阵Sw:
  • 
  • 计算类间散度矩阵SB：
  • 
  • 求解特征值问题：

• 选择投影方向：
  • 选取最大的几个特征中对应的特征向量作为投影方向
• 投影数据：
  • 将原始数据投影到这些方向上，得到降维后的数据
  • 多分类学习：
    • 拆解法：
      • 将多分类任务拆为多个二分类任务求解，.具体来说，先对问题进行拆分，然后为拆出的每个二分类任务训练一个分类器;在测试时，对这些分类器的预测结果进行集成以获得最终的多分类结果.
      • 拆分策略：
        • 一对一（OvO），一对其余（OvR），多对多（MvM）
        • OvO：OvO将这N个类别两两配对,从而产生N ( N - 1)/2个二分类任务,例如OvO将为区分类别Ci和Cj训练一个分类器，该分类器把D中的Ci类样例作为正例，Cj类样例作为反例.在测试阶段，新样本将同时提交给所有分类器，于是我们将得到N ( N - 1)/2个分类结果,最终结果可通过投票产生：即把被预测得最多的类别作为最终分类结果.
        • OvR：OvR则是每次将一个类的样例作为正例、所有其他类的样例作为反例来训练N 个分类器.在测试时若仅有一个分类器预测为正类，则对应的类别标记作为最终分类结果
        • 
        • 对比：
          • OvR只需训练N个分类器，而OvO需训练N （N  - 1）/2个分类器，因此，OvO的存储开销和测试时间开销通常比OvR更大.但在训练时,OvR的每个分类器均使用全部训练样例，而OvO的每个分类器仅用到两个类的样例，因此，在类别很多时，OvO的训练时间开销通常比OvR更小.
        • MvM：是每次将若干个类作为正类,若干个其他类作为反类，选择类可使用ECOC，即纠错输出码：
          • 编码：对N个类别做M次划分，每次划分将一部分类别划为正类，一部分划为反类,从而形成一个二分类训练集；这样一共产生M个训练集,可训练出M个分类器
          • 解码：M个分类器分别对测试样本进行预测，这些预测标记组成一个编码.将这个预测编码与每个类别各自的编码进行比较,返回其中距离最小的类别作为最终预测结果
          • 类别划分通过“编码矩阵”指定：二元码（正类反类）/三元码（正类反类停用类）
          • 
          • 优点：ECOC编码对分类器的错误有一定的容忍和修正能力，对应同一个学习任务，ECOC编码越长，纠错能力越强
  • 类别不平衡问题：
    • 定义：分类任务中不同类别的训练样例数目差别很啊的情况。
    • 解决方法：
      • 再缩放：m−表示反例数目m+表示正例数目
      • 
    • 这个方法是基于“训练集是真是样本总体的无偏采样”，三种方法：
      • 欠采样：第一类是直接对训练集里的反类样例进行“欠采样”(undersampling),即去除一些反例使得正、反例数目接近，然后再进行学习
      • 过采样：对训练集里的正类样例进行“过采样"(oversampling),即增加一些正例使得正、反例数目接近，然后再进行学习
      • 阈值移动：第三类则是直接基于原始训练集进行学习，但在用训练好的分类器进行预测时将

  • 

  • 嵌入到决策过程中

  • 10.多类特征线性回归

    

    ====》

    

    用函数表示：

    

    ==》向量化

    

    具有多个变量J（w，b）的成本函数的方程，w和x是多个特征的向量

    

    

    多元回归的梯度下降：

    

    11.特征缩放：

    特征在不同值的范围内时，对他们进行缩放，使其具有彼此可比的价值范围，使算法更快收敛。

    方法一：除最大值

    

    方法二：平均归一化

    

    方法三：Z分数归一化

    

    12.学习曲线：

    

    每次迭代后，代价函数应该下降，若没有，则表示𝛼：学习率过大，或程序出现bug

    梯度下降算法收敛所需要的迭代次数根据模型的不同而不同，我们可以通过绘制迭代次数和代价 函数的图来观察算法在何时趋于收敛。如果在一次迭代中, J ( θ ) 的值小于𝜀, 则可以说此次迭代是收敛的。

    若𝛼过小：则需要多次迭代才可收敛

    若𝛼过大：则J总不下降，永不会收敛

    选择 时, 可以尝试 … , 0.001 , 0.003 , 0.01 , 0.03 , 0.1 , 0.3 , 1 , … 等值

    13.多项式回归

    线性回归提够了一种构建以下形式模型的方法：

    

    

    14.Logistic回归算法：

    它适用于标签取值离散的情况，它的输出值永远在0到1之间

    二元分类：

    只有两种可能的几个，是（y=1）（正类）/否（y=0）（负类），

    

    公式：

    

    图像：

    

    损失函数：

    

    ====》

    

    y=1时，代价几乎为0

    

    

    梯度下降：

    

    15.决策边界：

    决策边界分为线性决策边界 (Linear decision boundary) 和非线性决策边界 (Non-linear decision boundary)。

    线性决策边界：

    

    非线性决策边界：

    

    决策边界是假设函数的一个属性，我们可以用非常复杂的模型来适应非常复杂形状的决策边界

    16.解决过拟合的方法

    搜集更多数据

    寻找特征值

    正则化：

    正则化线性回归和梯度下降：

    

    

    正则化逻辑回归和梯度下降 ：

    

    17.神经网络（书）：

  • 神经网络中最基本的成分是神经元模型。
  • M-P神经元模型：在这个模型中，神经元接收到来自几个其他神经元传递过来的输入信号，这些输入信号通过带权重的连接(connection)进行传递，神经元接收到的总输入值将与神经元的阈值进行比较，然后通过激活函数处理以产生神经元的输出
    • 
  • 常用Sigmoid函数作为激活函数：
    • 它把可能在较大范围内变化的输入值挤压到（0，1）输出值范围内。

  • 

  • 感知机：
    • 感知机由两层神经元组成，输入层接收外界输入信号后传递给输出层，输出层是M-P神经元（阈值逻辑单元）。
    • 
    • 感知机能容易的实现逻辑与或非运算
    • 
    • 
    • 学习规则：
      • 对于训练样例（x，y)，若当前感知机的输出为y，则感知机权重如此调整：
        • 𝜔i←𝜔i+∆𝜔i
        • ∆𝜔i=𝜂（y−y）xi
        • 𝜂∈（0，1）被称为学习率，若感知机对训练样例（x，y）预测正确，即y=y，则感知机不发生编号，否则将根据错误的程度进行权重调整
    • 感知机只有输出层神经元inx激活函数处理，即只用于一层功能神经元，学习能力有限
    • 若两类模式是线性可分的，即与或非问题，那么存在一个线性超平面能将它们分开，感知机的学习过程一定会收敛而求得𝜔
      • 
    • 解决非线性可分问题：
      • 使用多层功能神经元
      • 输入层和输出层之间的神经元，被称为隐层或隐含层，隐含层和输出层神经元都是拥有激活函数的功能神经元
      • 
    • 多层前反馈神经网络：
      • 每层神经元与下一层神经元全互连，神经元之间不存在同层连接，也不存在跨层连接。
      • 输入层神经元接受外界输入，隐层和输出层的神经元对信号进行加工，最后由输出层神经元输出
      • 
  • 误差逆传播算法（BP算法）：
    • 工作流程：
      • 先将输入示例提供给输入层神经元，然后逐层将信号前传，直到产生输出层的结果；然后计算输出层的误差(第4 - 5行)，再将误差逆向传播至隐层神经元(第6行),最后根据隐层神经元的误差来对连接权和阈值进行调整(第7行).该迭代过程循环进行，直到达到某些停止条件为止。
    • 目标：最小化训练集D上的累积误差
    • 标准BP算法每次更新只针对单个样例
    • 累积BP算法直接针对累计误差最小化，它在读取整个训练集D一遍后才对参数进行更新，更新频率低
    • 
  • 

  • 

    

    

  • 缓解BP算法过拟合的方法：
    • 第一种策略是“早停”(early stopping):将数据分成训练集和验证集，训练集用来计算梯度、更新连接权和阈值，验证集用来估计误差，若训练集误差降低但验证集误差升高，则停止训练，同时返回具有最小验证集误差的连接权和阈值.
    • 基本思想是在误差目标函数中增加一个用于描述网络复杂度的部分，例如连接权与阈值的平方和.仍令Ek表示第k个训练样例上的误差，W i表示连接权和阈值，则误差目标函数改变为
    • 
    • 其中𝜆∈（0，1）用于对经验误差与网络复杂度这两项进行折中，常通过交叉验证法来估计

  • 17.神经网络：

    定义： 

    它是一种模仿动物神经网络行为特征进行分布式并行信息处理的算法数学模型。这种网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的。神经网络的分支和演进算法很多种，从著名的卷积神经网络CNN，循环神经网络RNN，再到对抗神经网络GAN等等。

    神经网络的工作原理：每一层都输入一个数字向量并对其应用一组逻辑回归单元，用于计算另一个数字向量，然后传递到另一层，知道得出输出值

    

    数据在TensorFlow中表示方式：

    

    构建神经网络：

    

     或：

    

    前向传播：

    

    如何实现前向传播：

    dense函数：

    这个函数的作用是在神经网络中执行前向传播（Forward Propagation），它模拟了一个全连接层（Dense Layer）的计算过程。在深度学习中，前向传播指的是从输入数据开始，逐层计算直至得出输出的过程。

    

    

    如何高效实现神经网络：

    使用矩阵乘法实现dense函数

    

    TensorFlow实现：

    

    这段代码是使用TensorFlow和Keras构建一个简单的神经网络模型的示例。以下是每部分的解释：

    1. **导入模块**：

       - `import tensorflow as tf` 导入TensorFlow库，这是一个用于机器学习和深度学习的开源框架。

       - `from tensorflow.keras import Sequential` 导入Sequential模型，这是一个线性的堆叠层的API。

       - `from tensorflow.keras.layers import Dense` 导入Dense层，这是全连接层，也是神经网络中最常用的基本层类型。

    2. **创建模型**：

       ```python

       model = Sequential([

           Dense(units=25, activation='sigmoid'),

           Dense(units=15, activation='sigmoid'),

           Dense(units=1, activation='sigmoid')

       ])

       ```

       创建一个Sequential模型，并添加三个Dense层。第一层具有25个神经元，第二层具有15个神经元，最后一层具有1个神经元。所有层都使用Sigmoid作为激活函数。

    3. **编译模型**：

       ```python

       from tensorflow.keras.losses import BinaryCrossentropy

       model.compile(loss=BinaryCrossentropy())

       ```

       编译模型，指定损失函数为二进制交叉熵。二进制交叉熵常用于二分类问题的评估。

    4. **训练模型**：

       ```python

       model.fit(X, Y, epochs=100)

       ```

       使用提供的输入X和标签Y训练模型，其中epochs参数设置为100，表示梯度下降的迭代次数。

    总结一下，这段代码主要做以下事情：

    - 导入必要的TensorFlow和Keras库；

    - 定义一个具有三层的神经网络模型，每层使用Sigmoid激活函数；

    - 设置二进制交叉熵作为损失函数；

    - 使用提供的数据X和Y训练模型，共进行100次迭代。

    注意：这里的`X`和`Y`应该替换为你自己的训练数据。`X`是输入特征，`Y`是对应的标签。如果你正在处理回归任务，你可能需要更改最后一个层的激活函数（例如，使用线性激活函数），或者选择适合回归问题的损失函数。

    激活函数：

    作用：引入非线性特性到网络中，使得网络能够学习和逼近复杂的函数映射

    

    二进制分类问题：Sigmoid函数

    y有正有负：Linear activation 函数

    y只能取非负值：ReLU函数

    18.Softmax:解决多类别分类：

    在多类别分类中，每个样本只属于一个类别。这意味着对于一个样本，它只能被分配到一组离散的类别集合中的一个类别。

    

    ==》公式：

    

    损失函数：

    

    实现 ：

    

    使用 SparseCrossEntropy(from_logits=True) 来代替 SparseCategoricalCrossEntropy()。这是因为 from_logits=True 参数告诉 Keras 直接使用 logit（未标准化的分数）而不是 softmax 输出来计算交叉熵损失。这样做的原因是，直接使用 logit 计算损失可以避免在计算过程中出现数值不稳定的情况，特别是在极端情况下，softmax 函数的输出可能非常接近 0 或 1，导致计算上的困难。

    19.多个输出的分类（多标签分类）：

    在多标签分类中，每个样本可以属于多个类别。也就是说，一个样本可以同时拥有多个标签。例如，图像分类问题中，一张图片可能既包含猫又包含狗，也可能既不包含猫也不包含狗。在这种情况下，类别之间不是互斥的，一个样本可以同时属于多个类别。

    

    多类别分类和多标签分类的区别：

    多类别分类：一个样本仅属于一个类别，类别之间是互斥的

    多标签分类：每个样本可以属于多个类别，类别之间不是互斥的

    20.优化算法，Adam算法：

    增大或减小𝛼使更快接近最小值

    

    实现代码：

    

    21.卷积层

    每个神经元只看一个有限区域

    优点：计算更快，只需要少量训练数据

    

    22.模型评估

    将数据集分为训练集和测试集，用测试集对模型进行评估

    最小化平方误差成本的线性回归训练和测试过程

    

    最小化平方误差成本的分类回归：

    

    23.模型选择：

    交叉验证集（Cross-validation Set）是机器学习和数据科学中用于评估模型性能的一种数据集划分方法的一部分。在典型的机器学习项目中，数据集通常被划分为三个主要部分：训练集（Training Set）、验证集（Validation Set）和测试集（Test Set）。

  • 训练集 (Training Set)：
    • 用于训练模型，即调整模型参数以学习数据中的模式。
  • 验证集 (Validation Set)：
    • 也被称为交叉验证集，用于调整超参数（如学习率、正则化参数等）和模型架构的选择，以避免过拟合。
    • 在模型训练过程中，验证集用于评估模型的泛化能力，并根据验证集上的性能调整模型以达到更好的泛化效果。
  • 测试集 (Test Set)：
    • 用于最终评估模型的性能，通常在模型训练完成后进行一次测试，以评估模型在未见过的新数据上的表现。

  • 交叉验证集的作用：

  • 减少偏差：通过使用交叉验证，可以更准确地估计模型在未知数据上的性能，因为它利用了更多的数据进行验证。
  • 提高稳定性：由于交叉验证使用了多次验证的结果，因此可以降低模型性能评估的波动性。
  • 避免过拟合：交叉验证有助于选择最适合的模型和超参数，避免在训练集上过度拟合。

  • 

    步骤：

    1.训练所有模型，获得最终参数，

    2.使用Jcv评估性能

    3.选择Jcv最小的模型

    4.使用测试机估计过程选择的模型有多好

    24.诊断偏差

    选择模型选择Jtrain和Jcv都低的

    

    方法：

    

    这张图展示了模型复杂度与训练误差Jtrain和交叉验证误差Jcv的关系，其中横坐标表示多项式阶数（degree of polynomial），也就是模型的复杂程度。图中展示了三种情况：高偏差（欠拟合）、高方差（过拟合）和高偏差和高方差（欠拟合和过拟合）。

    1. **高偏差（欠拟合）**：

       - 图中红色曲线表示随着多项式的阶数增加，训练误差（$J_{train}$）和交叉验证误差（$J_{cv}$）都逐渐减小。

       - 高偏差意味着模型过于简单，无法捕捉数据的真实趋势。

       - 在这种情况下，$J_{train}$ 和 $J_{cv}$ 相近，因为两者都很高。

       - 文字注释指出：“High bias (underfit)”，并且强调“$J_{train}$ will be high”。

    2. **高方差（过拟合）**：

       - 图中绿色曲线表示随着多项式的阶数增加，训练误差（$J_{train}$）先下降然后上升，而交叉验证误差（$J_{cv}$）持续上升。

       - 高方差意味着模型过于复杂，导致在训练数据上表现良好但在新数据上表现不佳。

       - 在这种情况下，$J_{train}$ 可能较低，而 $J_{cv}$ 很大。

       - 文字注释指出：“High variance (overfitting)” 并强调 “$J_{cv} ≫ J_{train}$”。

    3. **高偏差和高方差**：

       - 图中蓝色曲线表示随着多项式的阶数增加，训练误差（$J_{train}$）和交叉验证误差（$J_{cv}$）都持续上升。

       - 这种情况同时具有欠拟合和过拟合的特点，模型既不能很好地捕捉数据的趋势又容易受到噪声的影响。

       - 在这种情况下，$J_{train}$ 和 $J_{cv}$ 都很高，而且 $J_{cv} ≫ J_{train}$。

  • 25.通过交叉验证选择𝜆

    

    通过交叉验证选择最佳的正则化参数 \( \lambda \) 是一种常用的方法，它可以确保所选模型既不过拟合也不欠拟合训练数据，并且能够在未见过的数据上表现良好。下面是通过交叉验证选择 \( \lambda \) 的一般步骤：

    1. **准备数据集**:

       - 将原始数据集划分为训练集、验证集和测试集。通常比例可以是 60% 训练集、20% 验证集、20% 测试集，或者使用其他比例。

       - 如果不需要最终测试集来评估模型的性能，可以使用 k-折交叉验证，此时数据会被划分为 k 个子集。

    2. **确定候选的 \( \lambda \) 值**:

       - 选择一系列 \( \lambda \) 的候选值。这些值应该覆盖从很小到很大的范围，例如 \( [0.001, 0.01, 0.1, 1, 10, 100] \)。

    3. **对于每个 \( \lambda \) 值**:

       - 使用训练集来训练模型，其中包含正则化项，其强度由 \( \lambda \) 控制。

       - 计算训练集上的损失（如均方误差 MSE）。

       - 计算验证集上的损失。

    4. **选择最佳 \( \lambda \) 值**:

       - 选取使验证集上的损失最小的那个 \( \lambda \) 值。这通常意味着在训练误差和验证误差之间找到了一个好的平衡点。

       - 这个 \( \lambda \) 值通常是使得验证误差最小的值，或者是在最小验证误差附近的一个值，以避免过拟合验证集。

    5. **最终模型评估**:

       - 使用选定的 \( \lambda \) 值重新训练模型，但这次使用整个训练集来进行训练。

       - 使用独立的测试集评估最终模型的性能，以得到一个不偏向于任何特定数据子集的泛化误差估计

    26.学习曲线：

    

    定义：

    学习曲线（Learning Curve）是机器学习中用于评估模型性能的一个重要工具。它通过绘制模型在不同大小的训练数据集上的性能，来帮助分析模型的学习能力、泛化能力和是否存在过拟合或欠拟合现象。

     学习曲线的基本概念：

    1. **训练误差**（Training Error）：

       - 表示模型在训练集上的预测误差。

       - 通常期望训练误差随训练集大小的增加而降低。

    2. **验证误差**（Validation Error）或**交叉验证误差**（Cross-Validation Error）：

       - 表示模型在验证集（或交叉验证集）上的预测误差。

       - 用于评估模型的泛化能力，即模型在未见过的数据上的表现。

       - 通常期望验证误差随训练集大小的增加而降低。

    3. **学习曲线图**：

       - 横轴通常表示训练数据集的大小。

       - 纵轴表示误差（通常为损失函数的值，如均方误差 MSE）。

       - 两条曲线分别表示训练误差和验证误差随训练数据集大小变化的趋势。

    学习曲线的典型形态：

    1. **高偏差（欠拟合）**：

       - 当训练误差和验证误差都很高，并且随着训练数据的增加，两条曲线都缓慢下降。

       - 这意味着模型太简单，不足以捕获数据中的复杂模式。

    2. **高方差（过拟合）**：

       - 当训练误差很低，但验证误差很高，并且两条曲线随着训练数据的增加逐渐收敛。

       - 这意味着模型在训练数据上表现很好，但在未见过的数据上表现不佳，即模型过拟合了训练数据。

    3. **良好的拟合**：

       - 当训练误差和验证误差都很低，并且两条曲线随着训练数据的增加趋于稳定。

       - 这意味着模型既能很好地拟合训练数据，也能很好地泛化到未见过的数据。

    27.解决问题方法：

    1. **获取更多的训练样本**：如果模型存在高方差（过拟合），那么添加更多的训练样本有助于减少模型对训练数据的过度敏感性，使其更好地泛化到新数据。这意味着模型在训练数据上表现得很好，但在测试数据上表现不佳。

    2. **尝试较小的特征集**：如果模型存在高偏置（欠拟合），减少特征数量可能有所帮助。这样可以使模型更加简单，更容易捕捉数据的主要趋势，从而提高整体性能。这意味着模型无法准确地拟合训练数据。

    3. **尝试添加额外的特征**：如果模型存在高偏置（欠拟合），添加额外的特征（如多项式特征）可能有助于提高模型的复杂度，使其更好地拟合数据。这同样适用于线性回归模型，因为添加多项式特征可以创建非线性的关系，从而更好地匹配数据分布。

    4. **尝试减小𝜆**：如果模型存在高偏置（欠拟合），减小正则化参数 𝜆 可能有助于提高模型的复杂度，允许它更好地拟合训练数据。这意味着模型过于简单，不能充分拟合数据。

    5. **尝试增大𝜆**：如果模型存在高方差（过拟合），增大𝜆可以通过增加正则化力度来限制模型的复杂度，防止它过度拟合训练数据。这意味着模型在训练数据上表现得很好，但在测试数据上表现不佳。

    25.添加数据：专注于添加更多类型的数据

    数据增强：

    数据增强（Data Augmentation）是一种常用的技术手段，旨在通过生成新的训练样本从而提高机器学习模型的性能和鲁棒性。它通过变换现有数据集中的样本，创造出额外的训练实例，这些实例虽然与原始数据有所差异，但仍然保持原有的分类标签或属性。数据增强特别适用于深度学习领域，尤其是计算机视觉任务，因为这些任务通常需要大量的训练数据来避免过拟合问题。

    数据增强的目的：

  • 减少过拟合：通过增加训练样本的多样性，可以使得模型更加泛化，减少对特定训练数据的依赖。
  • 提高模型性能：更多的数据意味着模型可以从更多角度学习特征，从而提高准确率。
  • 节约成本：相比收集新数据，数据增强是一种成本更低的方法。

  • 常见的数据增强技术：

  • 图像变换：
    • 旋转：随机旋转图像一定的角度。
    • 缩放：随机放大或缩小图像。
    • 平移：水平或垂直移动图像。
    • 翻转：沿水平轴或垂直轴翻转图像。
    • 裁剪：从图像中随机裁剪出一个区域。
    • 亮度调整：改变图像的亮度。
    • 色彩变化：更改图像的饱和度、对比度等颜色属性。
    • 噪声添加：在图像中加入随机噪声。
    • 模糊处理：使用高斯模糊等滤镜处理图像。
  • 文本数据增强：
    • 同义词替换：用同义词替换词语。
    • 句子扩展：通过添加描述性的短语来扩展句子。
    • 随机删除：随机删除句子中的某些词。
    • 随机交换：随机交换句子中相邻词的位置。
    • 文本插值：将两个句子混合在一起创建新的句子。
  • 语音数据增强：
    • 速度变化：改变音频的速度。
    • 音高变换：改变音频的音高。
    • 背景噪声：在音频中添加背景噪声。
    • 混响效果：模拟不同环境下的声音效果。
  • 其他类型的数据：
    • 时间序列数据：可以通过滑动窗口、数据平移等方式进行增强。
    • 结构化数据：可以通过添加噪声、采样等方式增强。

  • 数据合成：

    数据合成（Data Synthesis）是指通过算法生成与原始数据具有相似统计特性的新数据的过程。这种方法可以用于多种目的，包括但不限于增加训练数据量、保护隐私、模拟未知数据分布等。数据合成对于解决数据稀缺问题、提高模型训练效果以及保护敏感信息等方面具有重要作用。

    数据合成的主要目的：

  • 增加训练数据量：通过生成额外的样本，可以帮助模型更好地学习特征，并且减少过拟合的风险。
  • 隐私保护：合成数据可以用来替代真实数据，在保证数据有用性的同时保护个人隐私。
  • 模拟未知数据：当某些类型的样本在实际数据集中很少出现时，可以通过数据合成来增加这类样本的数量，提高模型对罕见情况的处理能力。

  • 26.决策树:

    定义：

    决策树模型是一种监督学习方法，常用于分类和回归任务。它通过一系列的判断规则来预测输出值。这些判断规则可以被可视化为一棵树结构，其中每个内部节点表示一个特征上的测试，每个分支代表一个测试结果，而每个叶节点代表一个类别（分类任务）或者一个数值（回归任务）

    

    决策树的构建过程：

  • 特征选择：选择最佳的特征来进行分割，使其有最大纯度。常用的特征选择度量有信息增益、增益率、基尼不纯度等。
    1. 纯净度测量：
       1. 熵 (Entropy)：熵是用来衡量一个集合的不确定性或混乱程度的度量。在二分类问题中，熵越低，表示节点越纯净。熵的计算公式为

  • 

    其中，p是正类的概率，1−p是负类的概率。当所有样本都属于同一类别时，熵为0；反之，当正负类各占一半时，熵最大。

  • 信息增益：

  • 它衡量的是使用某个特征进行划分后，数据集的熵或者基尼不纯度的减少量

  • 公式：

  • 

    

  • 如果信息增益较大，则说明使用该特征划分能显著降低数据集的熵（或基尼不纯度），因此值得进行划分。相反，如果信息增益较小，则说明使用该特征划分的效果并不明显，可以选择其他特征。

  •  

  • 树的生成：递归地根据选定的特征对数据进行划分，直到满足停止条件（比如达到最大深度、最小样本数量等）。
  • 何时停止分裂：
  • 当一个节点属于同一类别的比例达到100%
  • 当分裂会导致树超过最大深度限制
  • 当纯净度得分改善低于阈值
  • 当节点内的样本数低于阈值
  • 剪枝：为了防止过拟合，可以通过预剪枝或后剪枝的方法来简化决策树的复杂度。

  • 

  • Start with all examples at the root node:
    • 决策树开始于根节点，所有的样本都位于根节点上。
  • Calculate information gain for all possible features, and pick the one with the highest information gain:
    • 计算所有可能特征的信息增益，并选择信息增益最高的特征作为划分依据。
  • Split dataset according to selected feature, and create left and right branches of the tree:
    • 根据所选特征将数据集划分为左右分支。
  • Keep repeating splitting process until stopping criteria is met:
    • 继续重复划分过程直到达到停止条件为止。
    • When a node is 100% one class:
      • 当一个节点只属于同一类时，停止划分。
    • When splitting a node will result in the tree exceeding a maximum depth:
      • 当划分会导致树的深度超过最大深度时，停止划分。
    • Information gain from additional splits is less than threshold:
      • 如果额外的划分带来的信息增益低于阈值，则停止划分。
    • When number of examples in a node is below a threshold:
      • 当节点中的样本数量低于阈值时，停止划分。

  • 热编码：

    热编码（One-Hot Encoding）是一种对分类变量进行数值化处理的方法，通常用于机器学习和数据预处理中。它将每个分类变量转换成一组二进制变量，其中每个二进制变量对应原始分类变量的一个可能取值。

    如何选择最佳分类点：

    

    方差降低量最大的是最佳分类点

    27.Bagging算法

    

  • 给定一个训练集，其大小为m。
  • 对于b=1到B（B是预设的bootstrap采样次数）：
    • 使用有放回的采样方法（即Bootstrap Sampling）创建一个新的训练集，该新训练集的大小仍然为m。
    • 在新的训练集上训练一颗决策树。

  • 最终，我们将得到B颗决策树，这些决策树的集合称为“Bagged Decision Tree”

    28.随机森林算法

    随机森林算法中用于增加决策树之间差异性的一个关键特性，即在构建每棵树时，在每个节点选择分裂特征时，不是考虑所有的特征，而是从可用的特征中随机选择一个子集。

  • Bootstrap 抽样： 首先，从原始训练数据集中利用有放回的方式（即 Bootstrap 抽样）抽取 n 个样本形成一个新的训练集。这一步骤会重复 B 次，生成 B 个不同的训练集。
  • 特征子集选择： 在构建每一棵决策树时，不是考虑所有的特征，而是在每次分割时只考虑一部分特征。对于分类问题，通常是选择 sqrt(m) 或者某个固定比例的特征（其中 m 是总特征数）。对于回归问题，可以选择更少的特征。这样做的目的是增加各决策树间的差异性，避免过度相关。
  • 构建决策树： 对于每一个由 Bootstrap 抽样产生的训练集，构建一棵决策树。在每个节点的分裂过程中，选择最优特征进行分割。这里所说的最优特征指的是根据某种准则（如信息增益、基尼指数等）选择的特征。
  • 预测/评估： 对于新的输入实例，每棵决策树都会给出一个预测结果。对于分类问题，可以通过投票决定最终类别；对于回归问题，则是对所有树的预测结果求平均。这样得到的预测结果比单独一棵决策树更为稳健。

  • 29.增强树算法：

  • 初始化权重：给每个训练样本分配一个相等的权重 wiwi​，通常取值为 1mm1​，其中 mm是训练集的大小。
  • 循环 b 次：
    • 训练第 b 棵树：使用带有替换的采样方法创建一个新的训练集，但是与随机森林不同，增强树不从所有样本中等概率选取，而是更倾向于挑选那些之前树分类错误的样本。这意味着那些被之前的树分类错误的样本将有更大的机会被选入新的训练集中。
  • 更新权重：根据第 b 棵树的分类结果重新调整样本权重。具体来说，正确分类的样本权重减小，错误分类的样本权重增大。

  • 30.使用XGBoost

    

    31.使用情景

    决策树和树集成：

  • 适用于表格型（结构化）数据：决策树和树集成对于具有明确特征和标签的结构化数据表现良好，比如数据库或电子表格形式的数据。这类数据通常包含有序的特征和数值或类别变量，非常适合进行分割和递归划分。
  • 不适合非结构化数据：然而，它们并不推荐用于处理非结构化的数据，如图像、音频和文本。这些类型的数据需要特殊的预处理和转换才能转化为结构化格式，以便决策树和树集成可以处理。
  • 速度快：决策树和树集成通常比其他复杂的学习算法更快，因为它们不需要大量的计算资源来进行训练和预测。这使得它们在实时应用和资源有限的情况下非常有用。
  • 可解释性强：小型的决策树相对容易被人理解，因为它们可以通过一系列的规则表示出来，而这些规则可以直接解释为什么某个特定实例被分到了某个类别或者预测了一个特定的结果。这对于需要解释模型行为的应用非常重要，特别是在监管严格或需要透明度的领域。

  • 神经网络：

  • 适用范围广：神经网络适用于各种类型的数据，包括表格型（结构化）和非结构化数据。这意味着它们可以处理数字、文本、图像、声音等各种形式的信息。相比于决策树和其他传统机器学习模型，神经网络能更好地处理非结构化数据，如图像和语音识别。
  • 速度较慢：由于神经网络的复杂性，它们可能会比决策树慢。这是因为它们涉及大量的参数优化和计算密集型操作，如矩阵乘法和激活函数的评估。不过，现代硬件的进步（如GPU加速）已经显著改善了运行时间。
  • 迁移学习：神经网络支持迁移学习，即利用预先训练好的模型来解决类似的任务。这大大减少了训练时间和所需的标注数据量，尤其是在数据稀缺的情况下。例如，你可以使用在ImageNet上训练过的卷积神经网络（CNN）作为基础模型，然后微调它以适应你的特定图像分类任务。
  • 多模型系统：当构建一个由多个模型共同工作的系统时，组合多个神经网络可能更容易。这可以通过级联、并行或其他方式实现，使各个网络专注于特定的任务，然后将结果整合到一个总体输出中。这种方式有助于提高系统的灵活性和准确性。

  • 32.聚类算法：

    聚类是一种无监督学习方法，它的目标是将相似的对象分组在一起，称为簇（cluster），使得同一簇内的对象彼此之间尽可能相似，而不同簇之间的对象则尽可能不同。聚类分析可以帮助我们发现数据中的模式和结构，而无需事先知道具体的标签或类别。聚类算法可以用来探索数据，发现数据的内在结构，也可以作为其他分析任务的预处理步骤，如降维和可视化。

    33.K-means

  • 初始化：选择k个点作为初始簇中心（质心），通常随机选取。
  • 分配：将每个对象分配到最近的簇中心所在的簇。
  • 更新：重新计算每个簇的新质心，即簇内所有对象的均值。
  • 重复：如果质心没有变化或达到最大迭代次数，则停止；否则回到第2步

  • 

     

    初始化：

    

  • 随机初始化：在每次迭代中，从数据集中随机选择k个样本作为初始质心。箭头指向的注释表明这些质心是随机选择的例子。
  • 运行K-means：使用选定的初始质心运行K-means算法，得到每个样本的簇归属（c^(i)）和新的质心（μ_1, ..., μ_K）。
  • 计算代价函数：根据簇归属和质心，计算代价函数J(c^(1), ..., c^(m), μ_1, ..., μ_K)，也称为失真。失真是衡量簇划分质量的指标，通常定义为所有样本到其所属簇中心的距离平方和。
  • 重复上述步骤：循环100次，每次都随机初始化K-means并计算失真。这样做的目的是找到具有最低失真的簇划分。

  • 选择K值：

    肘部法：

    绘制失真（ distortion 或 inertia）随k增加的变化曲线，选择“肘部”处的k值。失真是所有样本到其所属簇中心的距离平方和。在k较小时，随着k的增加，失真下降很快；当k超过某个值后，失真下降缓慢。这个转折点对应的k值被视为最佳k值。

    

  • 训练下一颗树：使用更新后的权重作为新训练集的权重，训练下一棵树。
  • 重复以上步骤，直至达到预定的树的数量B。