【每日刷题】Day96

🥕个人主页:开敲🍉
🔥所属专栏:每日刷题🍍
🌼文章目录🌼
1. LCP 44. 开幕式焰火 - 力扣(LeetCode)
2. 1022. 从根到叶的二进制数之和 - 力扣(LeetCode)
3. 563. 二叉树的坡度 - 力扣(LeetCode)

1. LCP 44. 开幕式焰火 - 力扣(LeetCode)
//思路:记数+递归。这个题目之前用C刷过,现在用C++复写一遍。
class Solution {
public:
void _numColor(TreeNode* root,int* hash,int& ans)
{
//遍历到空返回
if(!root)
return;
//如果当前焰火颜色没有被记录过,则焰火颜色种类+1
if(!hash[root->val])
ans++;
//将遍历到的每一个焰火颜色记录,防止重复
hash[root->val]+=1;
_numColor(root->left,hash,ans);
_numColor(root->right,hash,ans);
}
int numColor(TreeNode* root)
{
int ans = 0;
int hash[1001] = {0};
_numColor(root,hash,ans);
return ans;
}
};
2. 1022. 从根到叶的二进制数之和 - 力扣(LeetCode)
//思路:递归+模拟栈。
//题目要求我们将树的每一条分支看作一个二进制数字,将所有分支的二进制数字的和返回。
//那么我们如何求得每一条分支的二进制数字呢?
//首先我们想到的是采用先序遍历的方法去遍历每一条分支,但是这里就有一个问题:我们如何区分不同分支代表的二进制数字呢?
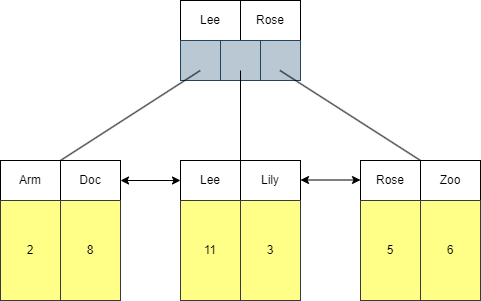
//这里我们采用栈的数据结构来解决这个问题,我们画图理解:

//这里又会有一个问题,当我们遍历完当前分支后,如何将栈顶数据推出呢?
//其实非常简单,我们只需要利用形参的特性就行了,看下面的实现代码。
class Solution {
public:
//判断是否为叶子节点
bool IsLeafNode(TreeNode* root)
{
return !root->left&&!root->right;
}
//注意到,这里的count我用的是形参,因为每次递归都会创建一个新的函数栈帧以存储当前的递归函数,因此每一个count都是独一无二的,比如上一层的count是1,这一层的count是2,当我们当前函数结束返回时,会返回到上一层的函数使用上一层的count也就是1,利用这个特性我们就能很好的实现不断更新栈顶数据。
void _sumRootToLeaf(TreeNode* root,int* Stack,int count,int& ans)
{
//如果为空直接返回
if(!root)
return;
//不为空则将当前val入栈
Stack[count] = root->val;
//如果为叶子节点则开始计算
if(IsLeafNode(root))
{
//次方
int flag = 0;
//从栈顶往栈底计算
for(int i = count;i>=0;i--)
{
ans+=pow(Stack[i]*2,flag);
//特殊处理0^0 = 1
if(!Stack[i]&&!flag)
ans-=1;
flag++;
}
return;
}
//线序遍历
_sumRootToLeaf(root->left,Stack,count+1,ans);
_sumRootToLeaf(root->right,Stack,count+1,ans);
}
int sumRootToLeaf(TreeNode* root)
{
int Stack[1001] = {0};
int ans = 0;
_sumRootToLeaf(root,Stack,0,ans);
return ans;
}
};
3. 563. 二叉树的坡度 - 力扣(LeetCode)
//思路:先序遍历+求和返回。
class Solution {
public:
int _findTilt(TreeNode* root,int& ans)
{
//空节点坡度为0
if(!root)
return 0;
//计算左子树的和
int ret1 = _findTilt(root->left,ans);
//计算右子树的和
int ret2 = _findTilt(root->right,ans);
//求坡度并相加
ans+=abs(ret1-ret2);
//返回左右子树的和+当前节点的val
return ret1+ret2+root->val;
}
int findTilt(TreeNode* root)
{
int ans = 0;
_findTilt(root,ans);
return ans;
}
};