摘要 解释计算机的错误计算(六十)中的错误计算原因。
计算机的错误计算(六十)中的计算可以归纳为 因此,我们只需要分析该算式。
例1. 已知 分析如何计算
首先,一个数乘以一个2,一般不会产生多少误差。另外,对于自变量为 内的数,我们假设函数
能得出正确值(比如起码15位正确数字,否则一切无意义)。
那么剩下的就只有 与
以及取余运算。
下面首先研究
类似于(五十二),利用错数进行讨论。由于
因此,
这样,
因此,函数要获得正确有效数字,
必须取到 97位有效数字。什么意思?比如,若只取到 96位正确有效数字,最后1位不正确:改正确数字0为1,则函数值为
而保留 3位有效数字的正确值是 0.983 . 所以, 的整数数字不能错 1位。若错了 1位,那么函数值就是错误结果。当然这时,后面也就不用分析了。
事实上,Python 是将
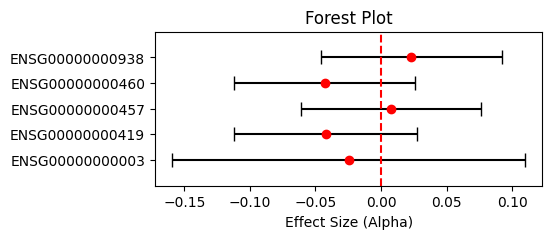
变成了64位的浮点数。根本不仅仅是错了 1位,而是错了几十位。从下图可以得到验证:

上图显示,若将自变量这个大整数变为浮点数,那么输出与(六十)中没有显式变为浮点数时的输出完全相同。所以,说明 Python在做取余运算时,隐式地做了变换。
我们可以从另外一个角度进行验证:

若只取 17位有效数字,那么取余后的值与(六十)中的余数完全相同。
您认可我的分析吗?待续。