目录

流程分析

归纳法分析

为什么是斐波那契数列？

推导过程：

解法1：循环累加计算

解法2：递归计算

解法3：利用数组特性

解法4：利用 JavaScript ES6 新特性

拓展知识：每次可以走 1 步、2 步、3 步

拓展知识：斐波那契数列

---

本题为 LeetCode第70题爬楼梯，题目如下：

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

大家可以先想想。

流程分析

本题中，可以每次可以走 1 级，也可以一次走 2 级，因此我们会有 3 种走法：

• 全程任意走，如全部 1 级走；
• 前面任意走，最后一步只走 1 级；
• 前面任意走，最后一步只走 2 级；

我画了几张图方便大家理解，如下：

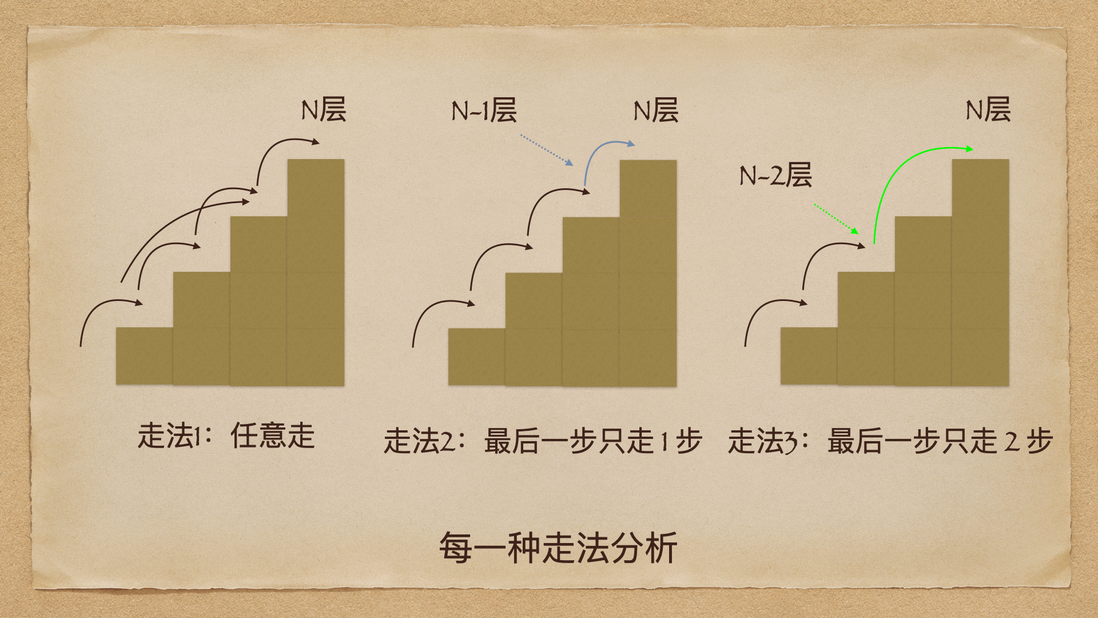
第一种走法就不做详细介绍。

第二种走法，倒数第二步的走法如下，有 1 步和 2 步两种方式：

第三种走法，倒数第二步的走法如下，也有 1 步和 2 步两种方式：

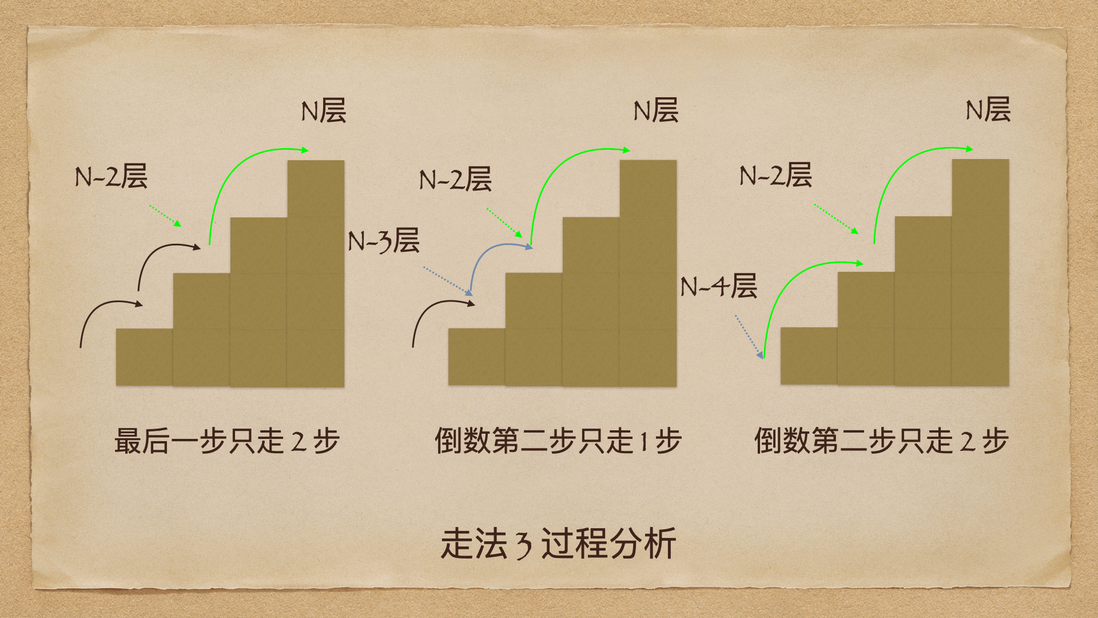
上面这个过程描述的是，从最后一层开始往下的每一层的走法。

在最后一步时，有 1 步和 2 步两种方式，可以理解为只能 1 步或者 2 步到达最后一层。

• 当最后一步为 1 步时，即从 n-1 层开始；
• 当最后一步为 2 步时，即从 n-2 层开始；

• 假设我爬1层还剩2 假设我爬2还剩1 那就是求 爬1级 和爬2级共有多少种 这个已知的

再理解一下这个过程，就是第 n 层的走法数量是第 n-1 层和第 n-2 层走法数量之和。

如果还不太理解，可以再看看前面的图。

归纳法分析

当然，遇事不决，归纳法走起，我们可以列举几种情况进行分析：

台阶层数	走法数量	走法
1	1	1
2	2	11、2
3	3	111、12、21
4	5	1111、112、121、211、22
5	8	11111、1112、1121、1211、2111、221、212、122
...	...	...

可以发现有个简单的规律，当台阶层数为 n 层，它的走法数量就有 n-1 层的走法数量加上 n-2 层的走法数量。

记做：f(n)=f(n-1)+f(n-2)。

想象一下，你站在楼梯的底部，楼梯顶部有n个台阶。你可以选择每次走1个台阶或者2个台阶。问题是，你有多少种不同的方法可以走到顶部。

为什么是斐波那契数列？

1. 第一步：如果你现在只有1个台阶（n=1），你只有一种方法，那就是直接走上去。所以，f(1)=1。
2. 第二步：如果你有2个台阶（n=2），你有两种方法：先走1个台阶再走1个台阶，或者直接走2个台阶。所以，f(2)=2。

推导过程：

• 当你走到第3个台阶（n=3）时，你可以从第1个台阶走两个2个台阶上来，或者从第2个台阶走一个1个台阶上来。所以，f(3)=f(2)+f(1)
• 同理，当你走到第4个台阶（n=4）时，你可以从第2个台阶走两个2个台阶上来，或者从第3个台阶走一个1个台阶上来。所以，f(4)=f(3)+f(2)

这个逻辑可以一直延续下去，每次你到达一个新的台阶，你可以选择从上一个台阶走1步上来，或者从上上一个台阶走2步上来。这就是为什么这个问题的解法是斐波那契数列，因为每一步的解都依赖于前两步的解。

简单来说，爬楼梯问题就像是你在玩一个数字游戏，每一步的“分数”都是前两步“分数”的和。这就是为什么我们说爬楼梯问题是斐波那契数列的一个实际应用。

解法1：循环累加计算

通过简单的循环累加就能得到结果：

const climbStairs = (n = 1) => {if (n <= 2) return n;let res = 0,n1 = 1,n2 = 2; // n1 表示前 2 项，n2 表示前 1 项for (let i = 3; i <= n; i++) {// 前两项值固定，因此从第 3 项开始循环res = n1 + n2;n1 = n2;n2 = res;}return res;
};

解法2：递归计算

按照 f(n)=f(n-1)+f(n-2)，这个方法更加简单：

const climbStairs = (n = 1) => {if (n <= 2) return n;return climbStairs(n - 1) + climbStairs(n - 2);
};

这个方法比较简洁易懂，但递归比较费时，容易出现 LeetCode 超出时间限制的提示。

解法3：利用数组特性

利用 f(n)=f(n-1)+f(n-2) 这个规律，先预设好前 2 项，再开始循环，最后返回数组最后一项即可：

const climbStairs = (n) => {let result = [1, 2];for (let i = 2; i < n; i++) {result.push(result[i - 1] + result[i - 2]);}return result[n - 1];
};

解法4：利用 JavaScript ES6 新特性

利用数组结构赋值操作： [a, b] = [c, d]：

const climbStairs = n => {let a = b = 1;for (let i = 0; i < n; i++) {[a, b] = [b, a + b];}return a;
};

拓展知识：每次可以走 1 步、2 步、3 步

这里多增加了一次可以走 3 步，这时候最后一步会有以下情况：

• 当最后一步为 1 步时，即从 n-1 层开始；
• 当最后一步为 2 步时，即从 n-2 层开始；
• 当最后一步为 3 步时，即从 n-3 层开始；

改造一下前面解法，还是一样：

const climbStairs = (n = 1) => {if(n <= 2) return n;if(n == 3) return 4;return climbStairs(n-1) + climbStairs(n-2) + climbStairs(n-3);
}

拓展知识：斐波那契数列

这一题主要考察的内容类似斐波那契数列（Fibonacci sequence）的计算，如果你还不清楚什么是斐波那契数列，这边先简单介绍一下，另外推荐

最早是有由数学家莱昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入的，数列大致如：0、1、1、2、3、5、8、13、21、34、....。
认真观察，我们可以发现一个规律：从第 3 项开始，每一项的值都等于前两项之和。

在自然界中，存在着许许多多的斐波那契数列的排列方式，比如一棵普通的树，它的树枝生长情况就像下面这样：

可以看到每一层枝干的数量为 1、2、3、5、8、...排列下去。当然还有很多其他的：

根据斐波那契数列的规律，得到这样的公式 f(n)=f(n-1)+f(n-2) 。跟我们前面列的差不多。