leetcode每日一题·买卖股票问题(Python)

买卖股票的最佳时机(股票最大利润)

题目链接
给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

暴力法

直接遍历两次，记录最大利润

class Solution:def maxProfit(self, prices: List[int]) -> int:max = 0for key,val in enumerate(prices):for j in prices[key+1:]:if j-val > max:max = j- valreturn max

执行代码可以通过，但是提交后报超时错误

一次遍历

一次遍历的思路为：遍历一遍数组，计算每次到当天为止的最小股票价格和最大利润。

class Solution:def maxProfit(self, prices: List[int]) -> int:minprice = float('inf')maxprofit = 0for price in prices:minprice = min(minprice, price)maxprofit = max(maxprofit, price - minprice)return maxprofit

买卖股票的最佳时机II

在买卖股票的最佳时机的基础上的升级版。
题目链接
给定一个数组 prices ，其中 prices[i] 是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

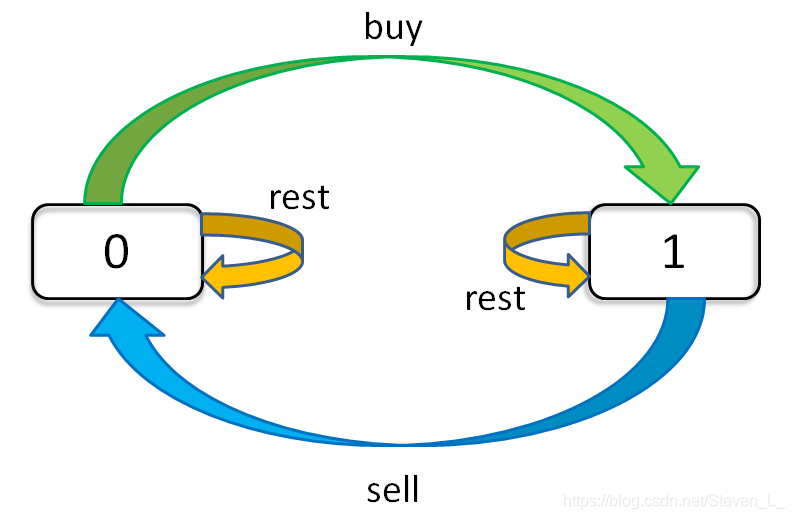
贪心算法

利用贪心算法，进行一次遍历，只要今天价格小于明天价格就在今天买入然后明天卖出，时间复杂度O(n)。

# 贪心算法，一次遍历o(n)
class Solution:def maxProfit(self, prices: List[int]) -> int:# 只要是第二天比第一天大就卖出ans = 0for i in range(1,len(prices)):if prices[i] > prices[i-1]:ans = ans + prices[i] - prices[i-1]return ans 

动态规划

DP动态规划，第i天只有两种状态，不持有或持有股票，当天不持有股票的状态可能来自昨天卖出或者昨天也不持有，同理，当天持有股票的状态可能来自昨天买入或者昨天也持有中，取最后一天的不持有股票状态就是问题的解。
这个方法没有学过DP的可能会理解起来比较困难，但是后边的两道升级版也要在这个基础上进行解决。

# 动态规划算法，一次遍历o(n)
class Solution:def maxProfit(self, prices: List[int]) -> int:if not prices:return 0n = len(prices)dp = [[0] * 2 for _ in range(n)]# dp[i][0]表示第i天不持有股票，dp[i][1]代表第i天持有股票dp[0][0], dp[0][1] = 0, -prices[0]for i in range(1, n):dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])return dp[n-1][0]