文章目录
- 像素的相邻像素
- 4邻域
- D邻域
- 8邻域
- 邻接、连通、区域和边界
- 邻接类型
- 连通
- 区域
- 边界
- 距离测度
- 欧氏距离
- 城市街区距离(city-block distance)
- 棋盘距离(chessboard distance)
- 参考
像素的相邻像素
4邻域
坐标 ( x , y ) (x,y) (x,y)处的像素 p p p有2个水平的相邻像素和2个垂直的相邻像素,它们的坐标是:
( x + 1 , y ) , ( x − 1 , y ) , ( x , y + 1 ) , ( x , y − 1 ) (x+1,y),(x-1,y),(x,y+1),(x,y-1) (x+1,y),(x−1,y),(x,y+1),(x,y−1)
这组像素称为 p p p的4邻域,用 N 4 ( p ) N_4(p) N4(p)表示。
D邻域
p p p的4个对角相邻像素的坐标是:
( x + 1 , y + 1 ) , ( x + 1 , y − 1 ) , ( x − 1 , y + 1 ) , ( x − 1 , y − 1 ) (x+1,y+1),(x+1,y-1),(x-1,y+1),(x-1,y-1) (x+1,y+1),(x+1,y−1),(x−1,y+1),(x−1,y−1)
这组像素称为 p p p的D邻域,用 N D ( p ) N_D(p) ND(p)表示。
8邻域
4邻域和D邻域合称为 p p p的8邻域,即 N 8 ( p ) = N 4 ( p ) + N D ( p ) N_8(p)=N_4(p)+N_D(p) N8(p)=N4(p)+ND(p)。点 p p p的相邻像素的图像位置集合称为 p p p的邻域,如果一个邻域包含 p p p,那么称该邻域为闭邻域,否则成为开邻域。
邻接、连通、区域和边界
令 V V V是用于定义邻接的灰度值集合。在二值图像中,指值为1的像素的邻接时, V = { 1 } V=\{1\} V={1}。在灰度图像中,这一概念相同,但集合 V V V通常包含更多的元素。例如,如果正在处理其值域为0到255的像素的邻接,那么集合 V V V可能是这256个值的任何一个子集。注意 V V V中的值可以不止一个,通常是一组相邻或相似的像素值集合。考虑三种类型的邻接:
邻接类型
- 4邻接: q q q在集合 N 4 ( p ) N_4(p) N4(p)中时,值在 V V V中的两个像素 p p p和 q q q是4邻接的。
- 8邻接: q q q在集合 N 8 ( p ) N_8(p) N8(p)中时,值在 V V V中的两个像素 p p p和 q q q是8邻接的。
- m m m邻接(也称混合邻接):满足以下两个条件之一
- q q q在 N 4 ( p ) N_4(p) N4(p)中。
- q q q在 N D ( p ) N_D(p) ND(p)中,但 N 4 ( p ) ∩ N 4 ( q ) N_4(p)\cap N_4(q) N4(p)∩N4(q)没有值在 V V V中的像素,那么值在V中的两个像素 p p p和 q q q是 m m m邻接的。
混合邻接用于消除8邻接的二义性。考虑下图的像素排列,并令 V = { 1 } V=\{1\} V={1}

左图采用8邻接时,中间的1和右上角的1之间存在两条通路。二者之间是8邻接的,但并不是m邻接的(因为二者的 N 4 N_4 N4有交集正上方的1),因此如果采用m邻接方式,则如右图所示,中间的1和右上角的1之间仅存在一条通路。
从坐标为 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)的像素 p p p到坐标 ( x n , y n ) (x_n,y_n) (xn,yn)的像素 q q q的数字通路(或曲线)是不同的像素序列,这些像素的坐标为:
( x 0 , y 0 ) , ( x 1 , y 1 ) , . . . , ( x n , y n ) (x_0,y_0),(x_1,y_1),...,(x_n,y_n) (x0,y0),(x1,y1),...,(xn,yn)
式中,点 ( x i , y i ) (x_i,y_i) (xi,yi)和点 ( x i − 1 , y i − 1 ) (x_{i-1},y_{i-1}) (xi−1,yi−1)在 1 ≤ i ≤ n 1\le i \le n 1≤i≤n时是邻接的。此时, n n n是通路的长度 ( x 0 , y 0 ) = ( x n , y n ) (x_0,y_0)=(x_n,y_n) (x0,y0)=(xn,yn)时,即起点和终点相同时,通路是闭合通路。
具体举例可以看参考链接。
在这里再提到一些最短通路的计算技巧:
- 8邻接中最短通路优先考虑斜线。
- m m m邻接中是在最短8通路的基础上,优先考虑斜线但需要考虑是否满足 m m m邻接的第二个条件。
- 4邻接中两个像素点是否存在通路可以通过看起点和终点是否有满足4邻接的像素点快速判断 。
连通
令 S S S表示图像中像素的一个子集。如果完全由 S S S中所有像素组成的两个像素 p p p和 q q q之间存在一个通路,那么称 p p p和 g g g在 S S S中是连通的。对于S中的任何像素 p p p,在 S S S中连通到该像素的像素集称为 S S S的连通分量。若S仅有一个连通分量,则集合S称为连通集。(表现为S中任意两个像素之间都是连通的)
区域
令 R R R表示图像中像素的一个子集。若 R R R是一个连通集,则称 R R R为图像的一个区域。两个区域 R i R_i Ri和 R j R_j Rj联合形成一个连通集时,称 R i R_i Ri和 R j R_j Rj为邻接区域。不邻接的区域称为不相交区域。谈到区域时,我们通常考虑的是4邻接和8邻接。如仅在使用8邻接时,下图的两个1值区域才是邻接的。
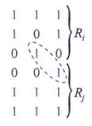
假设一幅图像含有 K K K个不相交的区域 R R R, k = 1 , 2 , ⋯ , K k=1,2,\cdots,K k=1,2,⋯,K,并且它们都不与图像边界相接。令 R u R_u Ru表示所有 K K K个区域的并集,并且令 ( R u ) c (R_u)^c (Ru)c表示其补集(集合A的补集是不在A中的点的集合)。我们称 R u R_u Ru中的所有点为图像的前景,而称 ( R u ) c (R_u)^c (Ru)c中的所有点为图像的背景。
边界
区域 R R R的边界(也称边框或轮廓)是 R R R中与 R R R的补集中的像素相邻的一组像素。换句话说,一个区域的边界是该区域中至少有一个背景邻点的像素集。这里,我们必须再次指定用于定义邻接的连通。例如,如果在区域及其背景之间使用4连通,那么下图中加圈的点就不是1值区域边界的成员。因为这个点和背景之间唯一可能的连接是对角线。为处理这种情况,一个区域及其背景中的点之间的邻接通常用8连通来定义。

前面的定义有时称为区域的内边界,以便与其外边界区分,外边界是背景中的对应边界。在开发跟踪边界的算法时,这一区别很重要。这种算法为了保证结果形成一个闭合通路,通常是沿外边界表达的。
距离测度
对于坐标分别为 ( x , y ) , ( u , v ) (x,y),(u,v) (x,y),(u,v)和 ( w , z ) (w,z) (w,z)的像素 p p p, q q q和 s s s,如果同时满足以下三个条件:
- D ( p , q ) ≥ 0 D(p,q) \ge 0 D(p,q)≥0 [ D ( p , q ) = 0 D(p,q) =0 D(p,q)=0,当且仅当 p = q p=q p=q]
- D ( p , q ) = D ( q , p ) D(p,q)=D(q,p) D(p,q)=D(q,p)
- D ( p , s ) ≤ D ( p , q ) + D ( q , s ) D(p,s) \le D(p,q)+D(q,s) D(p,s)≤D(p,q)+D(q,s)
则 D D D是一个距离函数或距离测度。
欧氏距离
p p p和 q q q之间的欧几里得(欧氏)距离定义为:
D e ( p , q ) = [ ( x − u ) 2 + ( y v ) 2 ] 1 2 D_e(p,q)=[(x-u)^2+(y_v)^2]^{\frac 1 2} De(p,q)=[(x−u)2+(yv)2]21
对于这个距离测度,到点 ( x , y ) (x,y) (x,y)的距离小于等于 r r r的像素,是中心在 ( x , y ) (x,y) (x,y)、半径为 r r r的圆盘。
城市街区距离(city-block distance)
p p p和 q q q之间的 D 4 D_4 D4距离(称为城市街区距离)定义为:
D 4 ( p , q ) = ∣ x − u ∣ + ∣ y − v ∣ D_4(p,q)=|x-u|+|y-v| D4(p,q)=∣x−u∣+∣y−v∣
此时,到 ( x , y ) (x, y) (x,y)的距离 D 4 D_4 D4小于等于 d d d的像素形成一个中心为 ( x , y ) (x,y) (x,y)的菱形。例如,到 ( x , y ) (x,y) (x,y)(中心点)的距离 D D D小于等于2的像素形成如下恒定距离的轮廓:
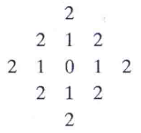
其中 D 4 = 1 D_4=1 D4=1的像素是 ( x , y ) (x,y) (x,y)的4邻域。
棋盘距离(chessboard distance)
p p p和 q q q之间的 D 8 D_8 D8距离(称为棋盘距离)定义为:
D 8 ( p , q ) = m a x ( ∣ x − u ∣ , ∣ y − v ∣ ) D_8(p,q)=max(|x-u|,|y-v|) D8(p,q)=max(∣x−u∣,∣y−v∣)
此时,到 ( x , y ) (x,y) (x,y)的距离 D 8 D_8 D8小于等于 d d d的像素形成一个中心为 ( x , y ) (x,y) (x,y)的正方形。例如,到中心点 ( x , y ) (x,y) (x,y)的距离 D D D小于等于2的像素形成如下恒定距离的轮廓:

其中 D 8 = 1 D_8=1 D8=1的像素是位于点 ( x , y ) (x,y) (x,y)处的像素的8邻域。
参考
数字图像处理(第四版)-冈萨雷斯
图像处理:像素间的一些基本关系(领域、领接性、通路、连通分量、距离)_m邻接-CSDN博客