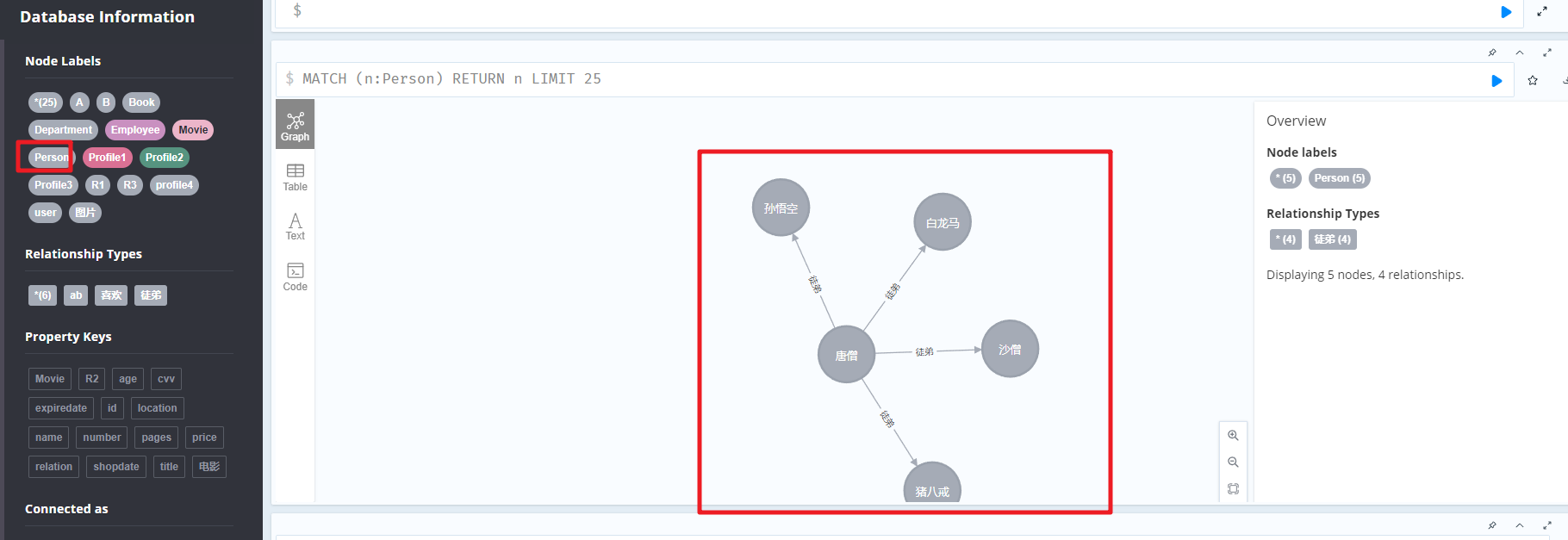
大家好,欢迎来到无限大的频道。
今日继续给大家带来力扣题解。
题目描述(简单):
与车相交的点
给你一个下标从 0 开始的二维整数数组 nums 表示汽车停放在数轴上的坐标。对于任意下标 i,nums[i] = [starti, endi] ,其中 starti 是第 i 辆车的起点,endi 是第 i 辆车的终点。
返回数轴上被车 任意部分 覆盖的整数点的数目。


解题思路:
这道问题抽象就抽象在,读不懂题目要求干啥,也不明白举例是什么意思,得先把题目看懂。(我来中译中一下)
这个问题可以理解为在数轴上有多辆车,每辆车的停车区域用一个区间来表示,例如 nums[i] = [starti, endi] 表示第 i 辆车的起点为 starti,终点为 endi。我们需要计算在数轴上这些车的停车区域重叠部分所覆盖的整数点的总数。
具体来说,我们需要求出所有车辆停车区间内的整数点的总和,即使得某一点被多辆车的区间覆盖也只算一次。
示例说明:
假设车辆的区间如下:
-
车1: [1, 3]
-
车2: [2, 5]
-
车3: [4, 6]
那么这些车辆覆盖的区间为:
-
车1覆盖的整数点为 {1, 2, 3}
-
车2覆盖的整数点为 {2, 3, 4, 5}
-
车3覆盖的整数点为 {4, 5, 6}
所有被覆盖的整数点为 {1, 2, 3, 4, 5, 6},所以被覆盖的整数点总数为 6。
算法思路:
-
合并区间:首先对所有区间进行合并,去掉重叠部分。
-
计算被覆盖的点:在合并之后计算每个区间中整数点的数量,即为 end - start + 1 的总和。
3.采用排序加贪心策略
参考代码:
// 定义一个结构体来表示区间
typedef struct {int start;int end;
} Interval;
// 比较函数用于排序
int compare(const void *a, const void *b) {Interval *intervalA = (Interval *)a;Interval *intervalB = (Interval *)b;return intervalA->start - intervalB->start;
}
int numberOfPoints(int** nums, int numsSize, int* numsColSize) {if (numsSize == 0) return 0;
// 1. 创建一个 Interval 数组Interval* intervals = (Interval*)malloc(numsSize * sizeof(Interval));
// 2. 将 nums 转换为 Interval 数组for (int i = 0; i < numsSize; i++) {intervals[i].start = nums[i][0];intervals[i].end = nums[i][1];}
// 3. 排序区间qsort(intervals, numsSize, sizeof(Interval), compare);
int totalPoints = 0;int currStart = intervals[0].start;int currEnd = intervals[0].end;
// 4. 合并区间并计算覆盖的点for (int i = 1; i < numsSize; i++) {if (intervals[i].start <= currEnd) { // 如果有重叠// 扩大当前区间的结束点if (intervals[i].end > currEnd) {currEnd = intervals[i].end;}} else { // 如果没有重叠,计算当前区间的点数totalPoints += currEnd - currStart + 1;currStart = intervals[i].start;currEnd = intervals[i].end;}}
// 添加最后一个区间的覆盖点totalPoints += currEnd - currStart + 1;
// 释放内存free(intervals);
return totalPoints;
}
时间复杂度:
1. 创建 Interval 数组:
创建 Interval 数组的时间复杂度是 O(n),其中 n是输入的区间数量 `numsSize`。
2. 将 nums 转换为 Interval 数组:
遍历所有区间并将其转换为 Interval 的时间复杂度同样是 O(n)。
3. 排序区间:
使用 `qsort` 进行排序,排序的时间复杂度是 O(n log n)。
4. 合并区间并计算覆盖的点:
遍历排好序的区间以合并并计算覆盖点的时间复杂度是 O(n)。
综上所述,主要的时间开销在于排序,因此整个 `numberOfPoints` 函数的时间复杂度为:
[O(n log n)]
空间复杂度:
1. 存储 Interval 数组:
创建存储 Interval 的数组需要 O(n)的额外空间。
2. 其他空间:
在函数中使用的变量、指针等只占用常数空间 O(1),不随 n 的变化而变化。
因此,整个函数的空间复杂度主要依赖于存储 Interval 数组的开销,为:
[O(n)]
总结:
时间复杂度:(O(n log n))
空间复杂度:(O(n))