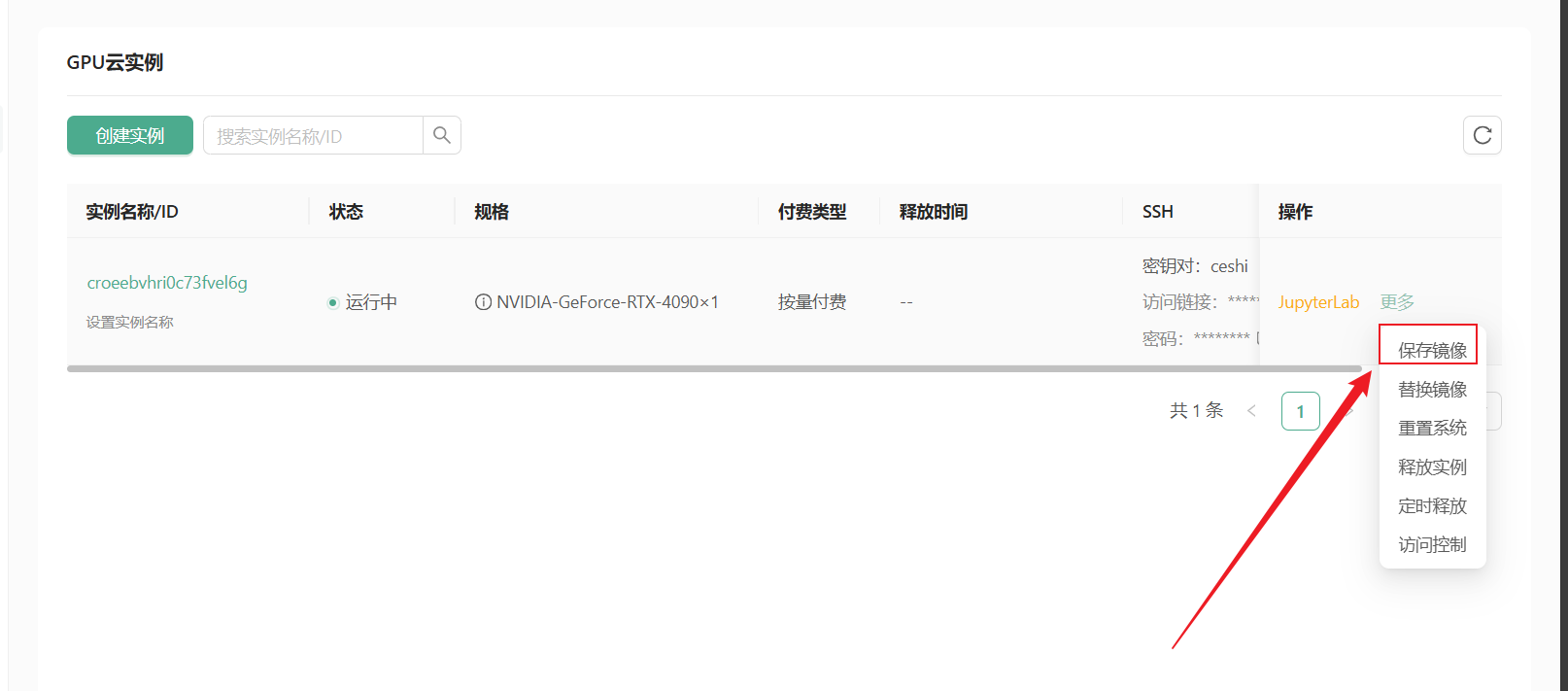
第八部分:贪心
561.数组拆分(简单)
题目:给定长度为 2n 的整数数组 nums ,你的任务是将这些数分成 n 对, 例如 (a1, b1), (a2, b2), ..., (an, bn) ,使得从 1 到 n 的 min(ai, bi) 总和最大。
返回该 最大总和 。
示例 1:
输入:nums = [1,4,3,2] 输出:4 解释:所有可能的分法(忽略元素顺序)为: 1. (1, 4), (2, 3) -> min(1, 4) + min(2, 3) = 1 + 2 = 3 2. (1, 3), (2, 4) -> min(1, 3) + min(2, 4) = 1 + 2 = 3 3. (1, 2), (3, 4) -> min(1, 2) + min(3, 4) = 1 + 3 = 4 所以最大总和为 4
示例 2:
输入:nums = [6,2,6,5,1,2] 输出:9 解释:最优的分法为 (2, 1), (2, 5), (6, 6). min(2, 1) + min(2, 5) + min(6, 6) = 1 + 2 + 6 = 9
第一种思路:
排序:首先,通过对输入数组
nums进行排序,使相邻的数能够成对配对,以最大程度保证 sum 的结果。初始化变量:定义一个变量
sum用于存储结果,left和right用于指向当前配对的元素。遍历并配对:
采用
while循环,确保right指针在数组范围内。在每次循环中,通过
Math.min(nums[left], nums[right])获取配对中较小的元素,并累加到sum中。由于nums已经排序,nums[left]和nums[right]就是形成配对的最小值。更新
left和right的位置,以移动到下一个待配对的元素。返回结果:当所有配对处理完毕后,返回最终的
sum。
class Solution { // 定义数组对和的求和方法 public int arrayPairSum(int[] nums) { // 先对数组进行排序 Arrays.sort(nums); int sum = 0; // 初始化和为0 int left = 0; // 左指针,指向当前配对的第一个数 int right = 1; // 右指针,指向当前配对的第二个数 // 当右指针没有超过数组边界时进行循环 while(right < nums.length) { // 每次配对取最小的数(即左指针的数),并累加到sum中 sum = sum + Math.min(nums[left], nums[right]); // 移动到下一个配对 left = right + 1; // 左指针移动到下一个配对的第一个数 right = left + 1; // 右指针移动到下一个配对的第二个数 } // 返回计算得到的和 return sum; }
} 另外补充(如果对这种思路的可行性有疑问):
分析这种思路的可行性时,我们需要理解题意以及排序的效果。题目要求组成一对数,最大化每对的最小值的总和。通过以下几个步骤,我们可以验证这种方法的有效性。
问题理解:
假设我们有一个数组,目标是将其分为 n 对 (ai, bi),然后求出所有对中最小值 (min(ai, bi)) 的总和。为了使这个总和最大,我们的目标是充分利用较大的数。
排序的思路:
排序的必要性:如果我们将数组进行排序,较小的数必然会靠前,较大的数会放在后面。这样在选取配对时,我们可以保证将较大的数与其紧邻的小数进行配对,从而让每对的最小值尽可能高。
合理配对:通过上述排序,我们可以采用每两个数一组的方式进行配对。对于已经排序的数组,配对
(nums[0], nums[1]), (nums[2], nums[3]), ...这样的方式,使得总和能够达到最大。因为:
对于每一对 (nums[i], nums[i+1]),min(nums[i], nums[i+1]) = nums[i],而 nums[i] 是这对中较小的元素。
因为 nums 是排序过的,nums[i] 的值会尽量大,确保较小的元素不会太小。
示例:
考虑一个简单的例子
[1, 4, 3, 2]:
排序后为
[1, 2, 3, 4]。配对方式为
(1, 2), (3, 4),最小值分别为1和3,因此总和为1 + 3 = 4。若我们不排序而随意配对,例如配对
(1, 3), (2, 4),最小值为1和2,总和为1 + 2 = 3,反而得不到最大值。结论:
通过以上分析,我们可以得出以下结论:
排序后按每两个数一组配对的做法,能确保每对的最小值最大化。
因此,这种配对方式是可行的,且可以满足题目要求,获得最大总和。
最终计算
由于我们通过遍历的方法直接计算每对的最小值并累加,这种方式保证了额外的效率,同时也完整利用了排序后的结构,最大化了总和。因此,返回的最大总和是可靠的。
整体上,排序并根据排序后的顺序组合元素构成的对,是解这个问题高效且合理的方法。
605.种花问题(简单)
题目:假设有一个很长的花坛,一部分地块种植了花,另一部分却没有。可是,花不能种植在相邻的地块上,它们会争夺水源,两者都会死去。
给你一个整数数组 flowerbed 表示花坛,由若干 0 和 1 组成,其中 0 表示没种植花,1 表示种植了花。另有一个数 n ,能否在不打破种植规则的情况下种入 n 朵花?能则返回 true ,不能则返回 false 。
示例 1:
输入:flowerbed = [1,0,0,0,1], n = 1 输出:true
示例 2:
输入:flowerbed = [1,0,0,0,1], n = 2 输出:false
第一种思路:
"判断能否在不打破种植规则的情况下在花坛内种入 n 朵花,从贪心的角度考虑,应该在不打破种植规则的情况下种入尽可能多的花,然后判断可以种入的花的最多数量是否大于或等于 n。" 链接:. - 力扣(LeetCode). - 备战技术面试?力扣提供海量技术面试资源,帮助你高效提升编程技能,轻松拿下世界 IT 名企 Dream Offer。
https://leetcode.cn/problems/can-place-flowers/solutions/542556/chong-hua-wen-ti-by-leetcode-solution-sojr/
变量初始化:
count:用于记录可以种植的花的数量。
m:花坛的长度。
prev:用于存储上一个花的位置,初始值为 -1 表示尚未找到种花的位置。遍历花坛:
使用一个循环遍历
flowerbed数组。当遇到种有花的位置(
flowerbed[i] == 1)时,进行以下操作:计算可以种花的数量:
如果
prev < 0,说明还没有种花,当前的位置是第一个花的位置。可以在从 0 到当前位置的空地中种花。通过i / 2计算可种花数。如果
prev >= 0,说明之前已经种过花。在当前位置与上一个花位置之间的空地上计算可以种植的花的数量,使用(i - prev - 2) / 2来获取可以种植的数量(要减去两个位置,因为中间需要有一个空地)。提前返回:
每当计算出
count后,立即判断是否已经大于等于 n,如果满足条件则返回true。处理未种花的情况:
循环结束后,检查是否还没有种花(
prev < 0),如果是,可以在整个花坛中种花,计算可种花数量为(m + 1) / 2(床的长度);如果
prev >= 0,则计算从最后一个花的位置到花坛结束之间可以种花的数量,使用(m - prev - 1) / 2。返回结果:
最后返回
count >= n,检查是否能够种下所需数量的花。对于第五步:处理未种花的情况
在遍历完整个
flowerbed数组后,我们需要根据是否种过花(有1的位置)来计算在剩余空地上可种植的花的数量。
如果
prev < 0:
这表明整个
flowerbed数组中都没有种花(即所有元素都是0)。在这种情况下,从花坛的开头到结尾都是可种植的空地。计算可种植的数量使用(m + 1) / 2
。这个数学公式的含义是:
例如,如果花坛长度为 5(即
m = 5),则有 6 个空地位置(例如0, 0, 0, 0, 0, 0),可以在位置0, 2, 4种花。具体的逻辑如下:
从第一个位置开始,每隔一个位置种一朵花,可以种下
(5 + 1) / 2 = 3朵花。如果
prev >= 0:
这表示花坛中至少种过一朵花(存在
1的位置)。需要计算从prev(最后一个种花的位置) 到花坛结束的位置之间的空地可以种植的花的数量:
为了保证新种花与现有花之间有空地,根据当前prev位置的计算,空地可以用(m - prev - 1) / 2计算。这是因为:
m - prev - 1是最后一个花和花坛结束之间的空地数量。为了在这些空地上种花,每种一个花后,下一个种的花又需要隔开一个空地,所以实际上可种下的花数量为
(空地数量) / 2。示例
假设
flowerbed为[0, 0, 0, 0, 0],即m = 5:
此时
prev < 0,可以种下(5 + 1) / 2 = 3朵花。假设
flowerbed为[1, 0, 0, 0, 1],此时prev最后指向的为 4:
计算
m - prev - 1为5 - 4 - 1 = 0,可以种花的数量为0 / 2 = 0,因此在最后的位置后没有空地可以种花。
class Solution { public boolean canPlaceFlowers(int[] flowerbed, int n) { int count = 0; // 记录可以种植的花朵数量 int m = flowerbed.length; // 获取花坛的长度 int prev = -1; // 用于记录最后一朵花的索引,初始为 -1 表示不存在 // 遍历花坛 for (int i = 0; i < m; i++) { // 当遇到已经种有花的位置 if (flowerbed[i] == 1) { // 如果之前没有花(prev < 0),可以在头部空地种花 if (prev < 0) { count += i / 2; // 从开头到当前位置,可以种的花的数量 } else { // 计算在 prev 到当前花之间的空地中可以种植的花 count += (i - prev - 2) / 2; // 要减去 2,因为需要一个空地隔开 } // 如果可种花数量已经大于等于 n,返回 true if (count >= n) { return true; } // 更新 prev 为当前花的位置 prev = i; } } // 处理没有种过花的情况 if (prev < 0) { // 如果整个花坛都是空地,可以在所有空地中种花 count += (m + 1) / 2; // 总空地数量的一半 } else { // 从最后一个花到花坛结束之间的空地 count += (m - prev - 1) / 2; // 计算可以种植的数量 } // 最终判断是否能够种下 n 朵花 return count >= n; }
}