写在前面

因为学弟已经问了几个题了，于是乎这场没有vp，准备直接开写了

题目

C. 种树（树形dp）

题解

只有两种情况，

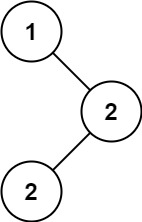
一种是1-2-3，1是2的父亲，2是3的父亲

另一种是1-2-3，2同时是1和3的父亲

所以树形dp从底往上合并即可

I. 找行李（线性dp）

题解

J. 找最小（线性基 分治）

题解

将ai^bi插入线性基，然后从高位往低位贪心，如果能令max(f(a),f(b))变小，则交换

证明

学弟的这个做法并不同官方题解，一开始学弟找了一个反例，

后来发现suma末位是1、sumb末位是0，没法做到让基里不出现1

于是，开始思考这样的正确性，是数据水了还是这个做法是正确的

想了近乎一天，最终认为它是对的，给一个证明

因为对称性，也就是说，

如果我用一些操作使得最终suma≤sumb，

我一定可以反选所有操作使得suma≥sumb

这意味着a和b的所有位都是可以互换的，只是有些位会有联动

从高到低，忽略不可操作的位后，遇到a和b都是1的，都消成0

而遇到a和b一个0一个1时，第一次不管换没换都是其中一个1一个0，

不妨是a为1，那么第二次以后全令b为1令a为0，

这样的贪心最小是可得的，并且只要第二次以后没按这个操作来，就会违反不等式

跃迁佬的补充：

只关心sa^sb的最高1位那步的正确性(其他显然)
由于sa^sb可被线性基表示,这组线性基(R)全反选相当于sa,sb互换(无效果)
于是这步可以直接乱选,反正万一选错了R内的其他基也反选就是

所以在sa^sb的最高1位那步可以直接rand

代码