1. Allen-Cahn方程

   考虑偏微分方程如下：
$$\begin{array}{r}\begin{array}{rl}& u_t-0.0001u_{xx}+5u^3-5u=0\\ & u(0,x)=x^{2}cos(\pi x)\\ & u(t,-1)=u(t,1)\\ & u_x(t,-1)=u_x(t,1)\end{array}\end{array}$$
其中$x\in [-1,1],t\in [0,1].$这是一个带有周期性边界条件，初始条件的偏微分方程。这个方程主要用$PIN{N}^{[1]}$论文中正向问题的离散时间模型求解。

2. 损失函数如下定义

$$\begin{array}{r}\begin{array}{r}SSE=SS{E}_n+SS{E}_b\end{array}\end{array}$$
其中
$$\begin{array}{r}\begin{array}{rl}SS{E}_n& =\sum _{j=1}^{q+1}\sum _{i=1}^{N_n}|u_j^n(x^{n,i})-u^{n,i}{|}^2\\ SS{E}_b& =\sum _{i=1}^q|u^{n+c_i}(-1)-u^{n+c_i}(1){|}^2+|u^{n+1}(-1)-u^{n+1}(1){|}^2\\ & +\sum _{i=1}^q|u_x^{n+c_i}(-1)-u_x^{n+c_i}(1){|}^2+|u_x^{n+1}(-1)-u_x^{n+1}(1){|}^2\end{array}\end{array}$$
这里$SS{E}_b$是周期性边界损失，$SS{E}_n$可以理解为PDE损失， { x n , i , u n , i } ∣ i = 1 N n \{x^{n,i},u^{n,i}\}|_{i=1}^{N_n} {xn,i,un,i}∣i=1Nn​​为$t^n$时刻相应的数据点和真解。$u_j^n(x^{n,i})$利用公式(4)、(5)计算得到。
$$\begin{array}{r}\begin{array}{rl}{u}^{n+c_i}& =u^n-\Delta t\sum _{j=1}^q{a}_{ij}\mathcal{N}[u^{n+c_j}],i=1,2,...,q\\ u^{n+1}& =u^n-\Delta t\sum _{j=1}^q{b}_j\mathcal{N}[u^{n+c_j}].\end{array}\end{array}$$
公式(4)中$\mathcal{N}[u^{n+c_j}]$表达式如公式(5)所示。
$$\begin{array}{r}\begin{array}{r}\mathcal{N}[u^{n+c_j}]=-0.0001u_{xx}^{n+c_j}+5(u^{n+c_j}{)}^3-5u^{n+c_j}\end{array}\end{array}$$
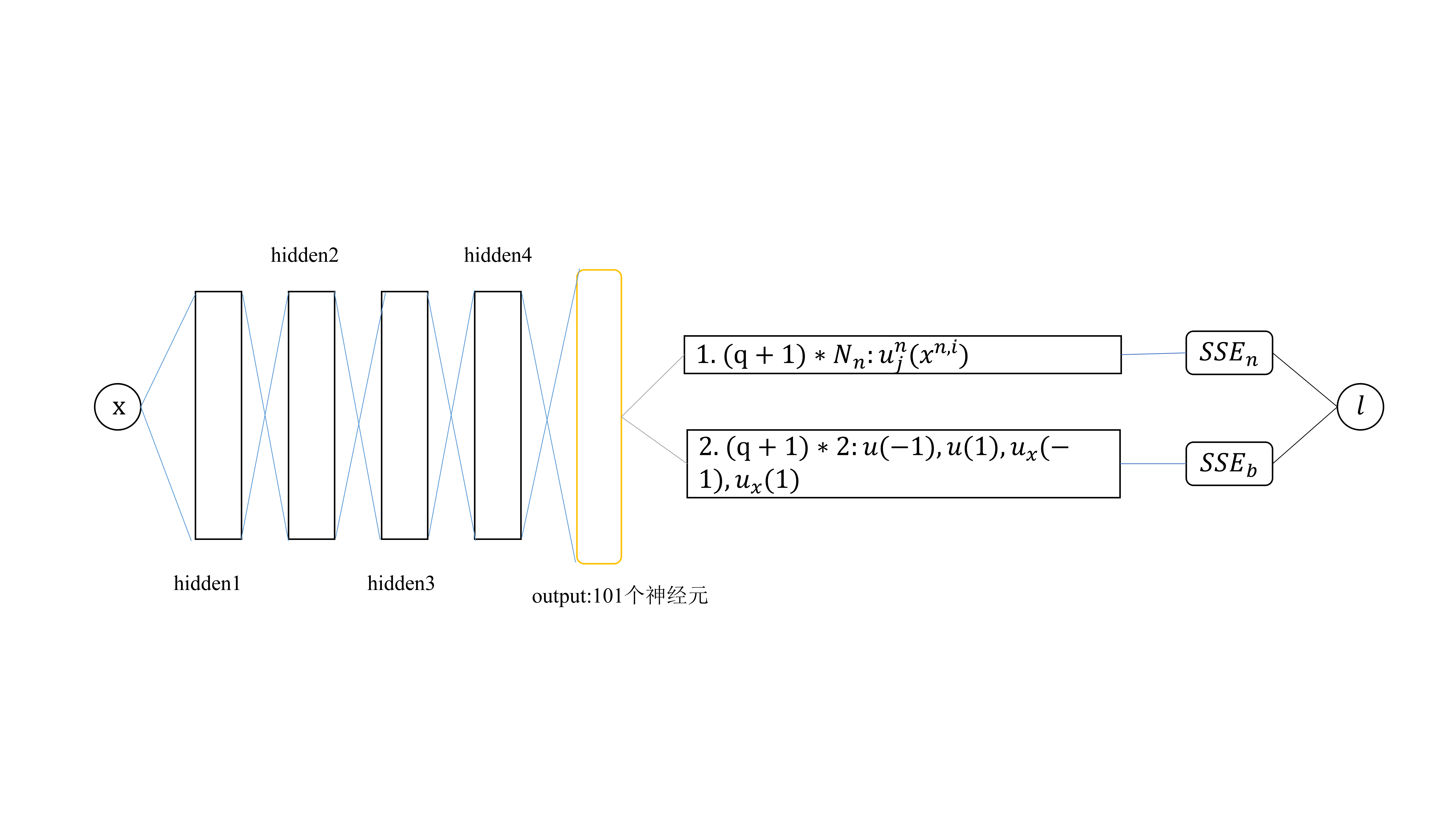
   这里$N_n=200，q=100，\Delta t=0.8$。神经网络模型输入层包括一个神经元，四个100神经元的隐藏层，101个神经元的输出层。

3. 代码

  代码参考下图进行理解。

  代码参考https://github.com/maziarraissi/PINNs,原代码运行框架tensorflow1，这里将其改为tensorflow2上运行，代码如下：

"""
@author: Maziar Raissi
@Annotator：ST
计算t*x为[0,1]*[-1,1]区域上的真解，真解个数t*x为201*256
"""import sys
sys.path.insert(0, '../../Utilities/')import tensorflow.compat.v1 as tf   # tensorflow1.0代码迁移到2.0上运行，加上这两行
tf.disable_v2_behavior()# import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import time
import scipy.io
from plotting import newfig, savefig
import matplotlib.gridspec as gridspec
from mpl_toolkits.axes_grid1 import make_axes_locatablenp.random.seed(1234)
tf.set_random_seed(1234)class PhysicsInformedNN:# Initialize the classdef __init__(self, x0, u0, x1, layers, dt, lb, ub, q):"""input: 200个t=0.1时x坐标，x=-1，1 输入202个样本output: 每个坐标输出这个坐标在未来q个时间的解和t+dt时刻的解，输出维度分别为(200*101)(2*101):param x0: 空间选定的200个点的x坐标值:param u0: 200个x在t=0.1时对应的u的精确解:param x1: 空间边界[[-1],[1]]:param layers: 神经网络各层神经元列表:param dt: 时间步长 0.8:param lb: -1:param ub: 1:param q: q阶龙格库达，即t方向取q个点的斜率的加权平均作为龙格库达法的平均斜率"""self.lb = lbself.ub = ubself.x0 = x0self.x1 = x1self.u0 = u0self.layers = layersself.dt = dtself.q = max(q,1)# Initialize NNself.weights, self.biases = self.initialize_NN(layers)# Load IRK weightstmp = np.float32(np.loadtxt('../../Utilities/IRK_weights/Butcher_IRK%d.txt' % (q), ndmin = 2))self.IRK_weights = np.reshape(tmp[0:q**2+q], (q+1,q))self.IRK_times = tmp[q**2+q:]# tf placeholders and graphself.sess = tf.Session(config=tf.ConfigProto(allow_soft_placement=True,log_device_placement=True))self.x0_tf = tf.placeholder(tf.float32, shape=(None, self.x0.shape[1]))self.x1_tf = tf.placeholder(tf.float32, shape=(None, self.x1.shape[1]))self.u0_tf = tf.placeholder(tf.float32, shape=(None, self.u0.shape[1]))self.dummy_x0_tf = tf.placeholder(tf.float32, shape=(None, self.q)) # dummy variable for fwd_gradientsself.dummy_x1_tf = tf.placeholder(tf.float32, shape=(None, self.q+1)) # dummy variable for fwd_gradientsself.U0_pred = self.net_U0(self.x0_tf) # N(200) x (q+1)  200个x内部点输入网络训练self.U1_pred, self.U1_x_pred= self.net_U1(self.x1_tf) # N1(=2) x (q+1)  x=-1,1 输入网络得到边界# self.U1_pred (2*101) 分别对应x=-1,1时的预测的dt内q个真解和一个u^{n+1}时的真解self.loss = tf.reduce_sum(tf.square(self.u0_tf - self.U0_pred)) + \tf.reduce_sum(tf.square(self.U1_pred[0,:] - self.U1_pred[1,:])) + \tf.reduce_sum(tf.square(self.U1_x_pred[0,:] - self.U1_x_pred[1,:]))                     # self.optimizer = tf.contrib.opt.ScipyOptimizerInterface(self.loss,#                                                         method = 'L-BFGS-B',#                                                         options = {'maxiter': 50000,#                                                                    'maxfun': 50000,#                                                                    'maxcor': 50,#                                                                    'maxls': 50,#                                                                    'ftol' : 1.0 * np.finfo(float).eps})self.optimizer_Adam = tf.train.AdamOptimizer()self.train_op_Adam = self.optimizer_Adam.minimize(self.loss)init = tf.global_variables_initializer()self.sess.run(init)def initialize_NN(self, layers):        weights = []biases = []num_layers = len(layers) for l in range(0,num_layers-1):W = self.xavier_init(size=[layers[l], layers[l+1]])b = tf.Variable(tf.zeros([1,layers[l+1]], dtype=tf.float32), dtype=tf.float32)weights.append(W)biases.append(b)        return weights, biasesdef xavier_init(self, size):in_dim = size[0]out_dim = size[1]        xavier_stddev = np.sqrt(2/(in_dim + out_dim))return tf.Variable(tf.truncated_normal([in_dim, out_dim], stddev=xavier_stddev), dtype=tf.float32)def neural_net(self, X, weights, biases):num_layers = len(weights) + 1H = 2.0*(X - self.lb)/(self.ub - self.lb) - 1.0for l in range(0,num_layers-2):W = weights[l]b = biases[l]H = tf.tanh(tf.add(tf.matmul(H, W), b))W = weights[-1]b = biases[-1]Y = tf.add(tf.matmul(H, W), b)return Ydef fwd_gradients_0(self, U, x):        g = tf.gradients(U, x, grad_ys=self.dummy_x0_tf)[0]return tf.gradients(g, self.dummy_x0_tf)[0]def fwd_gradients_1(self, U, x):        g = tf.gradients(U, x, grad_ys=self.dummy_x1_tf)[0]return tf.gradients(g, self.dummy_x1_tf)[0]def net_U0(self, x):U1 = self.neural_net(x, self.weights, self.biases)U = U1[:,:-1]U_x = self.fwd_gradients_0(U, x)U_xx = self.fwd_gradients_0(U_x, x)F = 5.0*U - 5.0*U**3 + 0.0001*U_xxU0 = U1 - self.dt*tf.matmul(F, self.IRK_weights.T)    # IRK_weights(101*100)  包括了Runde-Kutta方法参数a，breturn U0def net_U1(self, x):U1 = self.neural_net(x, self.weights, self.biases)U1_x = self.fwd_gradients_1(U1, x)return U1, U1_x # N x (q+1)def callback(self, loss):print('Loss:', loss)def train(self, nIter):tf_dict = {self.x0_tf: self.x0, self.u0_tf: self.u0, self.x1_tf: self.x1,self.dummy_x0_tf: np.ones((self.x0.shape[0], self.q)),self.dummy_x1_tf: np.ones((self.x1.shape[0], self.q+1))}start_time = time.time()for it in range(nIter):self.sess.run(self.train_op_Adam, tf_dict)# Printif it % 10 == 0:elapsed = time.time() - start_timeloss_value = self.sess.run(self.loss, tf_dict)print('It: %d, Loss: %.3e, Time: %.2f' % (it, loss_value, elapsed))start_time = time.time()# self.optimizer.minimize(self.sess,#                         feed_dict = tf_dict,#                         fetches = [self.loss],#                         loss_callback = self.callback)def predict(self, x_star):U1_star = self.sess.run(self.U1_pred, {self.x1_tf: x_star})return U1_starif __name__ == "__main__": q = 100layers = [1, 200, 200, 200, 200, q+1]lb = np.array([-1.0])ub = np.array([1.0])N = 200data = scipy.io.loadmat('../Data/AC.mat')t = data['tt'].flatten()[:,None]  # T(201) x 1  精确解时间坐标节点x = data['x'].flatten()[:,None]  # N(512) x 1  精确解空间坐标节点Exact = np.real(data['uu']).T  # T x N 精确解idx_t0 = 20idx_t1 = 180dt = t[idx_t1] - t[idx_t0]    # 时间步长0.8# Initial datanoise_u0 = 0.0idx_x = np.random.choice(Exact.shape[1], N, replace=False)    # 随机选择空间200个点的下标索引x0 = x[idx_x,:]    # 空间200个点的x坐标值u0 = Exact[idx_t0:idx_t0+1,idx_x].T    # t=0.10时200个精确解u0 = u0 + noise_u0*np.std(u0)*np.random.randn(u0.shape[0], u0.shape[1])# Boudanry datax1 = np.vstack((lb,ub))# Test datax_star = xmodel = PhysicsInformedNN(x0, u0, x1, layers, dt, lb, ub, q)model.train(2)    # 10000U1_pred = model.predict(x_star)    # (512,101)error = np.linalg.norm(U1_pred[:,-1] - Exact[idx_t1,:], 2)/np.linalg.norm(Exact[idx_t1,:], 2)print('Error: %e' % (error))  # sqrt(sum_{i=1}^512 (u-u_{ext})) / sqrt(sum_{i=1}^512 (u_{ext}))  相对误差################################################################################################### Plotting #####################################################################################################    fig, ax = newfig(1.0, 1.2)ax.axis('off')####### Row 0: h(t,x) ##################    gs0 = gridspec.GridSpec(1, 2)gs0.update(top=1-0.06, bottom=1-1/2 + 0.1, left=0.15, right=0.85, wspace=0)ax = plt.subplot(gs0[:, :])h = ax.imshow(Exact.T, interpolation='nearest', cmap='seismic', extent=[t.min(), t.max(), x_star.min(), x_star.max()], origin='lower', aspect='auto')divider = make_axes_locatable(ax)cax = divider.append_axes("right", size="5%", pad=0.05)fig.colorbar(h, cax=cax)line = np.linspace(x.min(), x.max(), 2)[:,None]ax.plot(t[idx_t0]*np.ones((2,1)), line, 'w-', linewidth = 1)ax.plot(t[idx_t1]*np.ones((2,1)), line, 'w-', linewidth = 1)ax.set_xlabel('$t$')ax.set_ylabel('$x$')leg = ax.legend(frameon=False, loc = 'best')ax.set_title('$u(t,x)$', fontsize = 10)####### Row 1: h(t,x) slices ##################    gs1 = gridspec.GridSpec(1, 2)gs1.update(top=1-1/2-0.05, bottom=0.15, left=0.15, right=0.85, wspace=0.5)ax = plt.subplot(gs1[0, 0])ax.plot(x,Exact[idx_t0,:], 'b-', linewidth = 2) ax.plot(x0, u0, 'rx', linewidth = 2, label = 'Data')      ax.set_xlabel('$x$')ax.set_ylabel('$u(t,x)$')    ax.set_title('$t = %.2f$' % (t[idx_t0]), fontsize = 10)ax.set_xlim([lb-0.1, ub+0.1])ax.legend(loc='upper center', bbox_to_anchor=(0.8, -0.3), ncol=2, frameon=False)ax = plt.subplot(gs1[0, 1])ax.plot(x,Exact[idx_t1,:], 'b-', linewidth = 2, label = 'Exact') ax.plot(x_star, U1_pred[:,-1], 'r--', linewidth = 2, label = 'Prediction')      ax.set_xlabel('$x$')ax.set_ylabel('$u(t,x)$')    ax.set_title('$t = %.2f$' % (t[idx_t1]), fontsize = 10)    ax.set_xlim([lb-0.1, ub+0.1])    ax.legend(loc='upper center', bbox_to_anchor=(0.1, -0.3), ncol=2, frameon=False)savefig('./figures/retest/reAC')

4. 实验细节及复现结果

  这里使用4层全连接神经网络，输入层和输出层各两个神经元，输入层一个神经元代表$x$坐标值，输出层101个神经元分别代表$[u^{n+c_1}(x),\cdots ,u^{n+c_q}(x),u^{n+1}(x)]$，隐藏层每层100个神经元。为了计算误差，作者提供了使用谱方法计算的$(256\ast 201)$个真解，其中第一维度代表空间$x$，第二维度代表时间$t$. 训练10000次之后输出结果如下：

It: 9970, Loss: 5.127e+00, Time: 0.08
It: 9980, Loss: 1.335e+01, Time: 0.07
It: 9990, Loss: 2.095e+01, Time: 0.07
Error: 2.470155e-01

这里误差是相对误差，计算公式如下：
$$\begin{array}{r}\begin{array}{r}Error=\frac{||U-U_{ext}|{|}_2}{||U_{ext}|{|}_2}\end{array}\end{array}$$
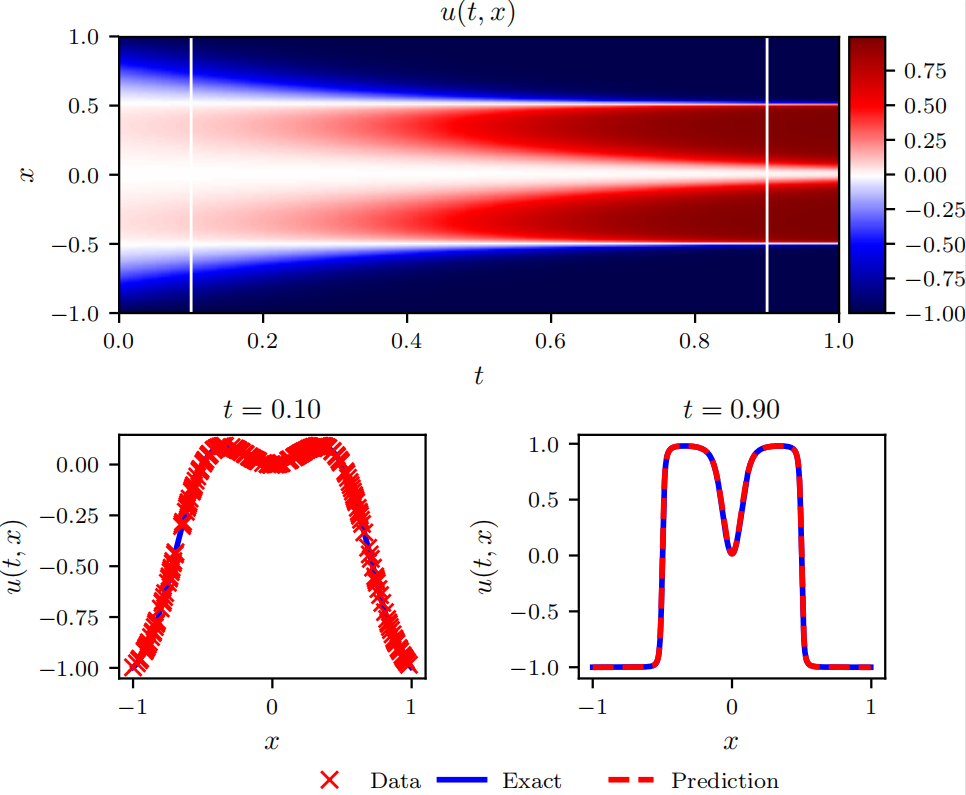
其中$U\in {\mathbb{R}}^{512\times 1},U_{ext}\in {\mathbb{R}}^{512\times 1}$,前者为$t=0.9$时PINN预测的解，后者为$t=0.9$时计算的精确解。复现结果图如下：

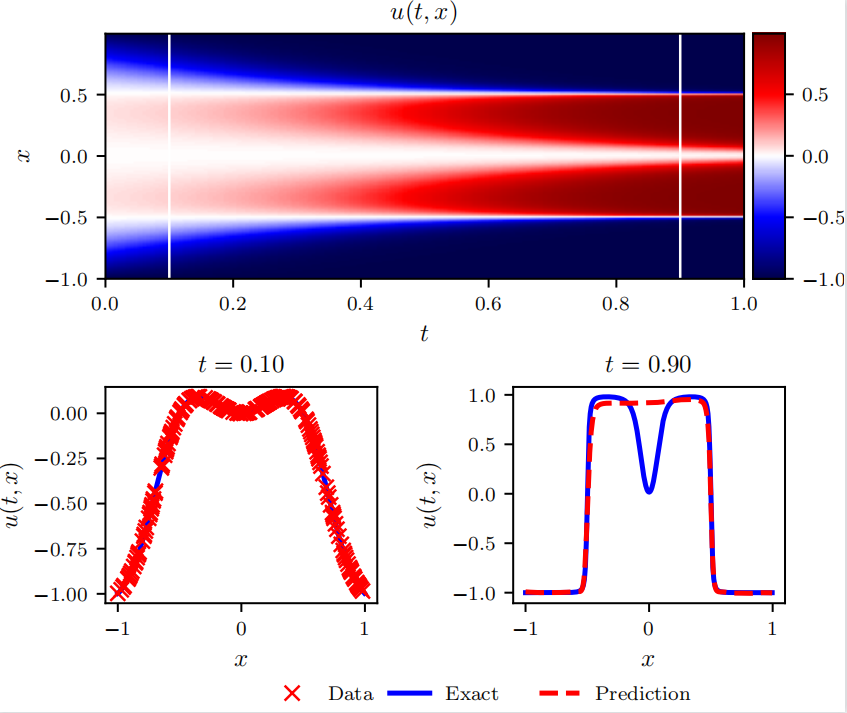
论文中结果如下：

参考资料

[1]. Physics-informed machine learning