DDD领域驱动设计批评文集
做强化自测题获得“软件方法建模师”称号
《软件方法》各章合集
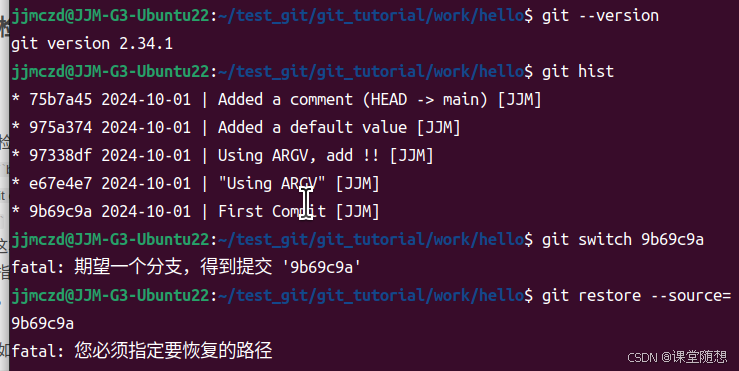
“Analysis Patterns”的第3章的图3.5,原文的图是:
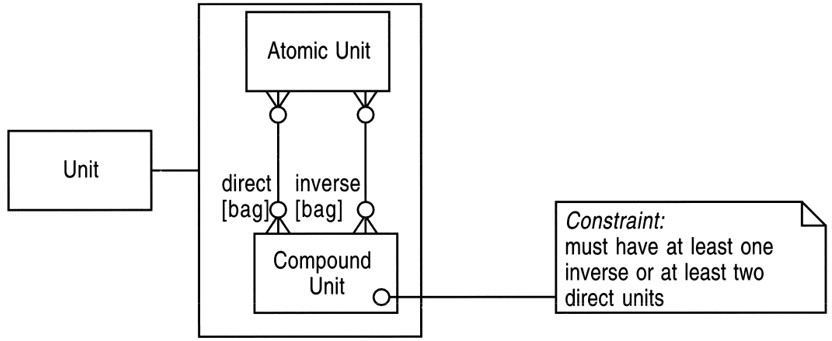
2004(机械工业出版社)中译本的图是:
direct翻译成分子,inverse翻译成分母。虽然不是直译,但意思是可以的。
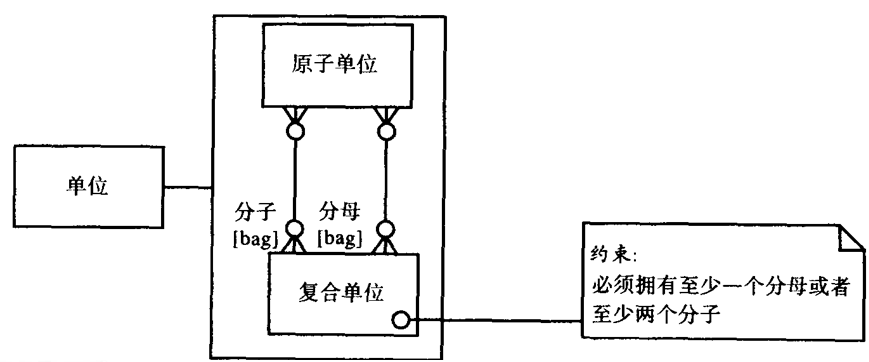
2020(人民邮电出版社)中译本的图是:
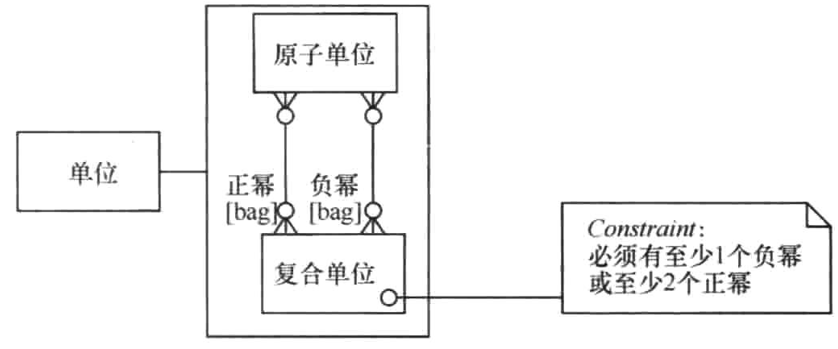
其他部分和2004中译本差不多,除了把direct翻译成正幂,inverse翻译成负幂。这个也不是直译,但意思是错的。原文没有“幂”,译者自行加上“幂”,导致内容出现了错误。
**********
首先我们来回顾“幂”的定义。


乘方:重复连乘的运算
幂:乘方的结果
b:基数
n:指数
接下来,得从图3.4来说起。
第3章讲的是“观察和测量”,其中有关于单位的模式。图3.4是单位的一个建模方案,原图如下:
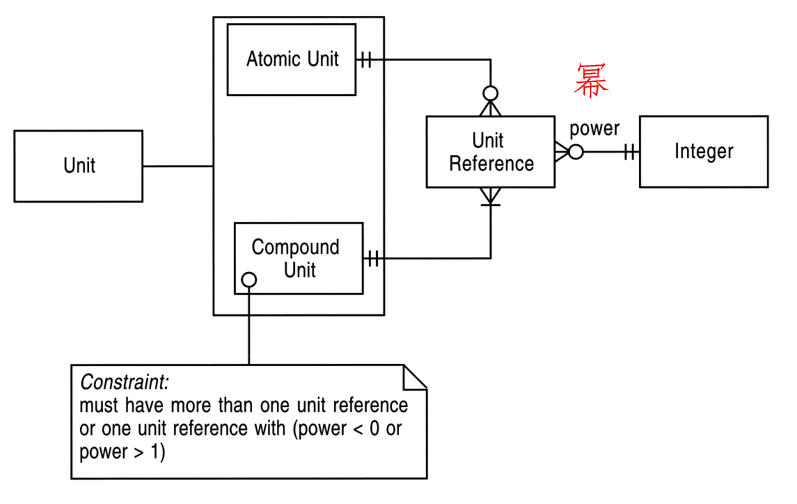
图上的power就是幂。
原子单位如千克(kg)、米(m)、秒(s)等,复合单位可以由原子单位组合而成,例如力的单位牛顿(N)和压强单位帕斯卡(Pa):
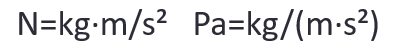
根据刚才回顾的幂的定义,模型需要记住的严格来说不是幂(power),而是指数(exponent),所以Fowler的原文在这里的表达是有点不恰当的,不过这个不是这次讨论的重点,所以后文我还是用“幂”。
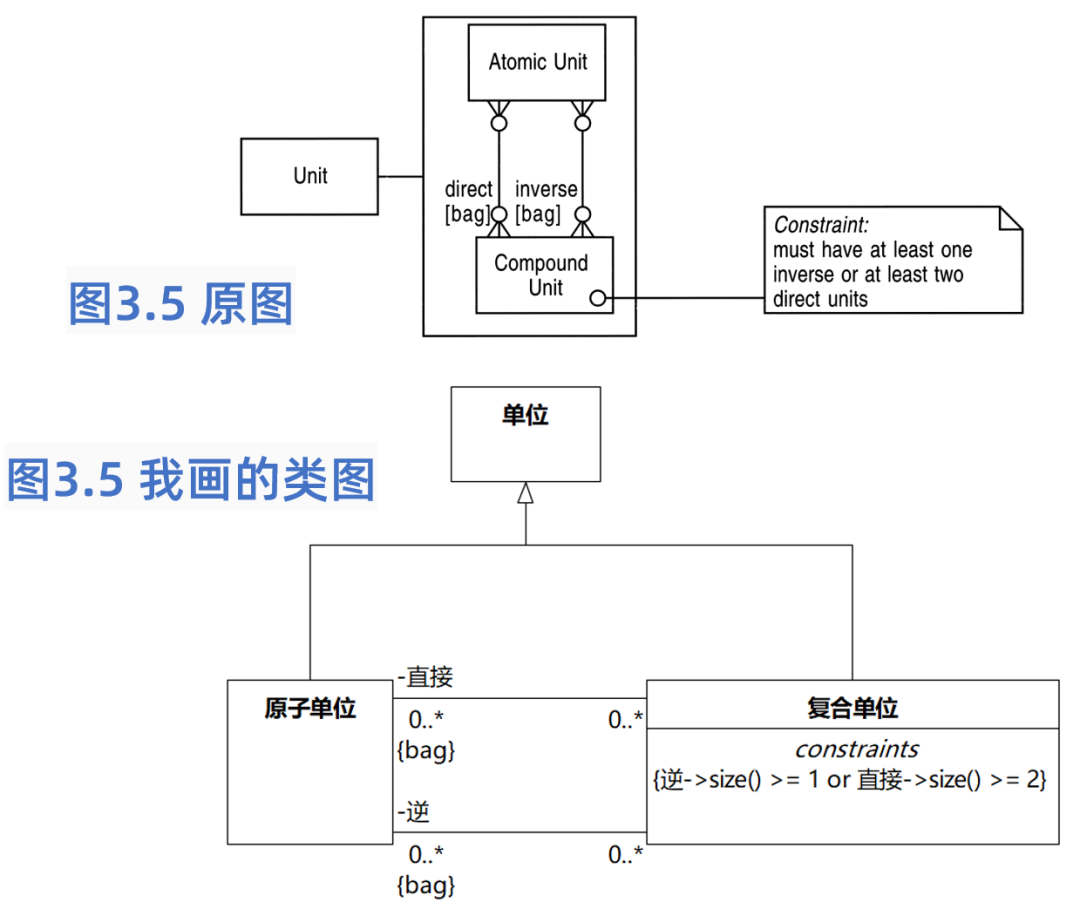
我把图3.4转成了如下的类图。“复合单位”的约束,在原文中是自然语言,我把它转成了OCL。
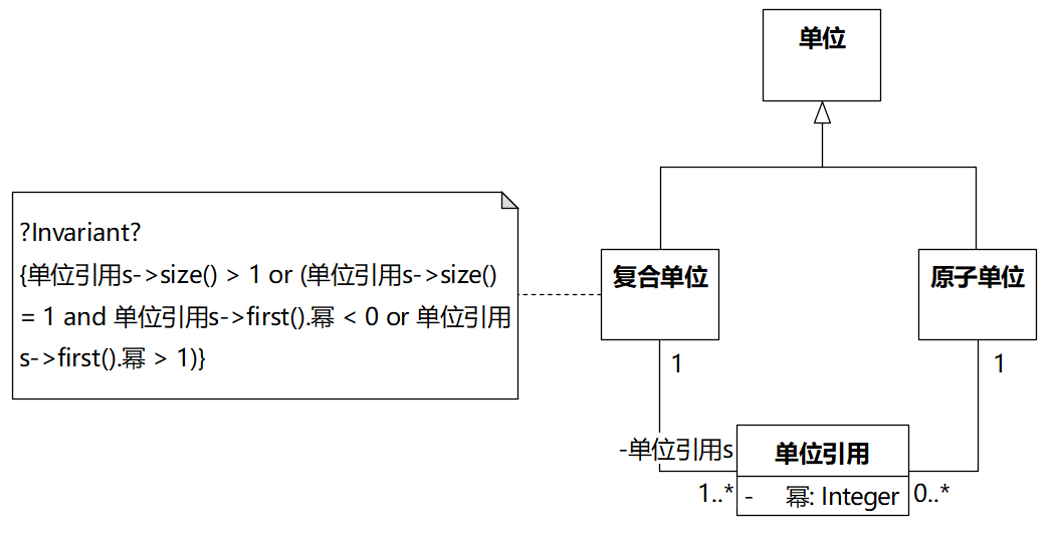
约束的意思:要么有多于一个的单位引用,例如“千克·米”,如果只有一个单位引用,例如,只有一个“米”,那么这个“米”的幂必须<0或>1,例如,米的-1次方或2次方。
我们把图3.4实例化,填上数据来看一下。

原子单位,填了3行,千克、米、秒,ID分别1、2、3;
复合单位,填了牛顿、焦耳、瓦特、帕斯卡,ID分别为24、56、66、88。
结合上文的图3.4以及牛顿(N)和帕斯卡(Pa)的定义,“单位引用”的数据如下:
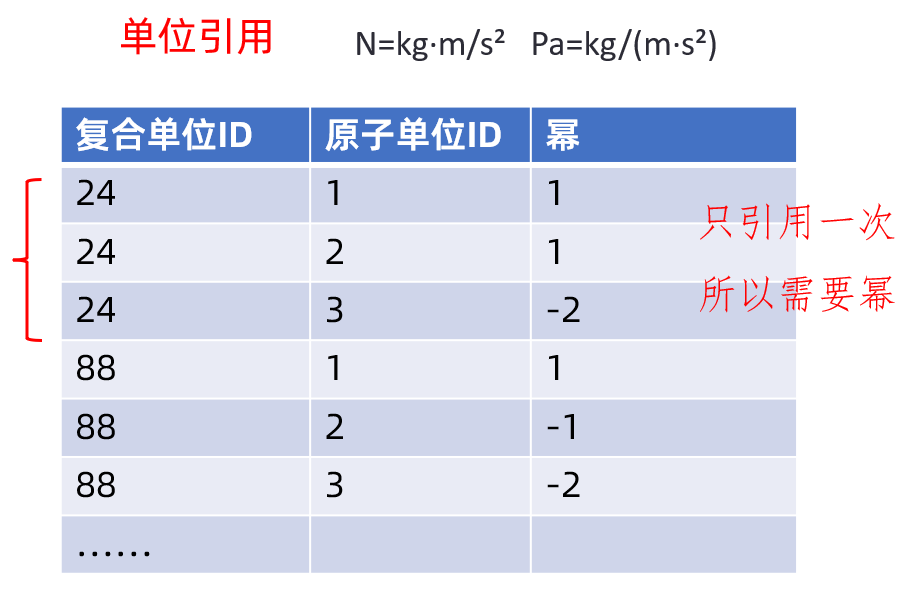
牛顿和帕斯卡都引用了三个原子单位(千克、米、秒),所以在“单位引用”中都有3行,只是“幂”这一列的值不同。即使复合单位的组合中有米的8次方,“米”在该复合单位的数据中仍然只占1行,只是“幂”的值是8。
我们来看图3.5,也就是刚才说2020中译本搞错了的那个图。
同样,我也把它画成了类图,和原图对比如下:
此时,已经没有“单位引用”这个类,而是在“复合单位”和“原子单位”之间有两个关联,一个是直接,一个是逆,相当于2004中译本的分子、分母。
“复合单位”的约束和图3.4也不一样了,我用同种颜色圈出它们的对应关系大致如下:
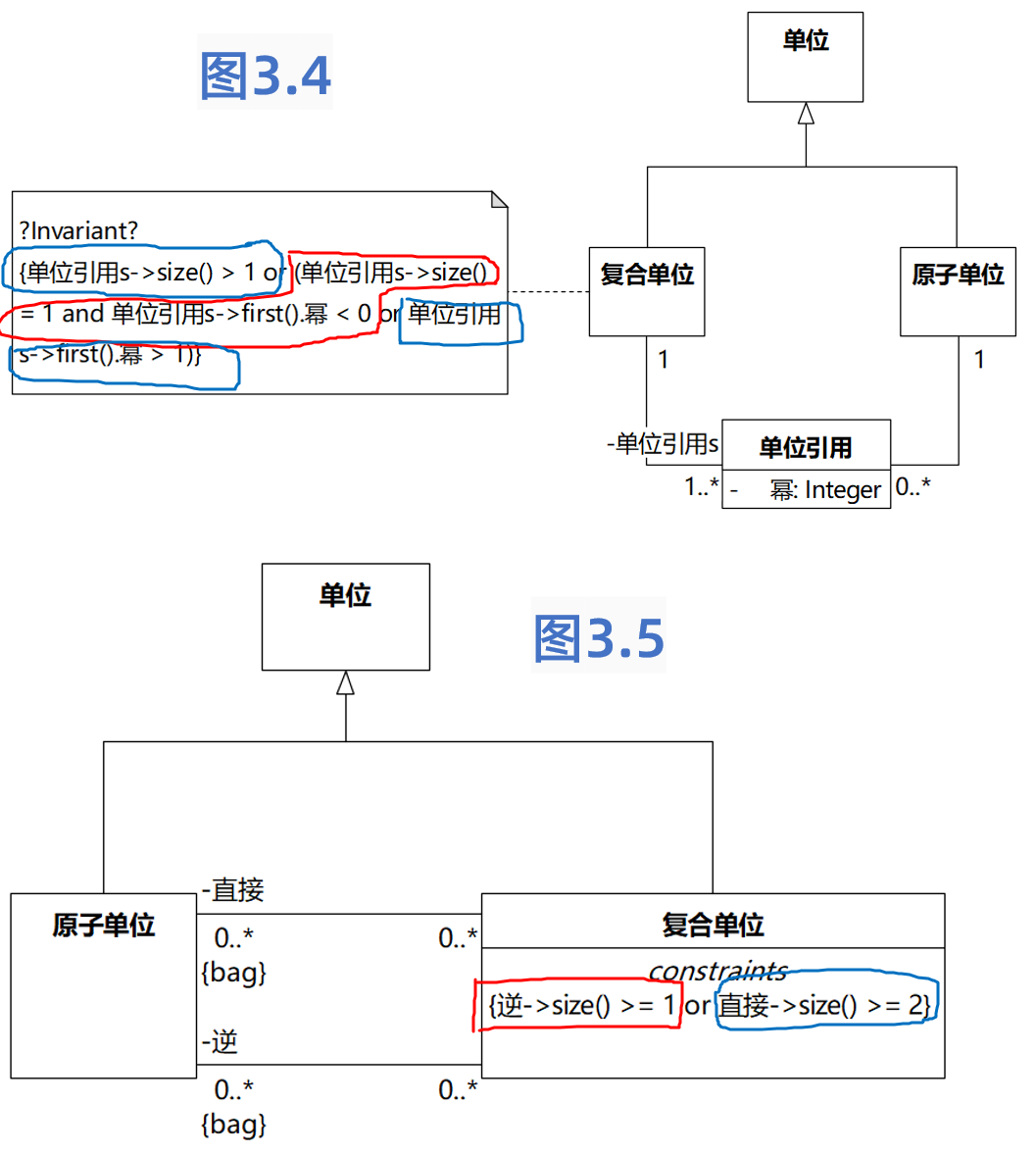
★建模工具中,在类图的关联某端选中“无序”、“可重复”选项,bag就会出现,不需要输入文字。
★Fowler原书的图,bag和direct、inverse的位置是错的,应该靠近“Atomic Unit(原子单位)”处,类似问题我在之前的文章中已指出。
同样,我们把图3.5实例化,填上数据来看一下。

上面这个部分和图3.4一样。
不同的是下面这个部分,没有“单位引用”了。取而代之的是两个关联,都是多对多的,于是有两个中间表“复合单位-直接原子单位”和“复合单位-逆原子单位”。
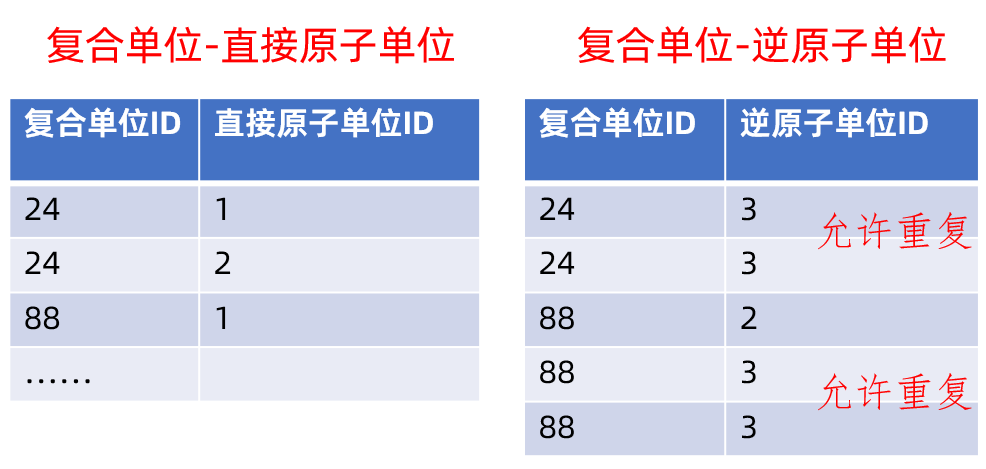
我们把图3.4的数据和图3.5的数据放在一起看其中的变化:
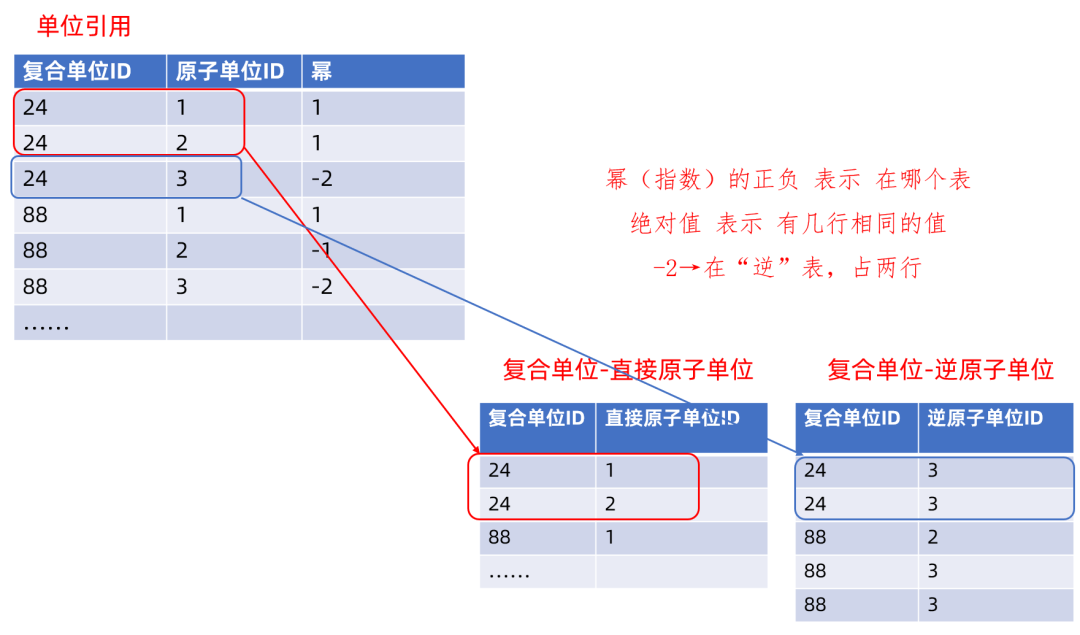
图3.4中幂(指数)的正负表示在图3.5的哪个表,绝对值表示在图3.5的表中有几行相同的值,例如,-2表示在“逆”表,占2行。
当然,使用关系数据库来保存,还需要添加标识,不能有完全一样的两行。
这时候,已经没有“幂”的概念了,不存在:

存在的是

或者

同一个原子单位也不一定要凑在一起,反正又不用凑成乘方。
在这一点上,Fowler原文的文字用得很精准。

你看他的用词,seconds and seconds(秒和秒),并没有说seconds squared(平方秒)之类。
**********
因此,2020中译本这个地方的内容,可以把“幂”去掉,直译“直接”、“逆”,或者按照机械工业出版社的“分子”、“分母”也可以。
还有另外一个小地方,“单元引用”应和上面一致,“单位引用”。